В основании одномерного разреза лежит пласт конечного

Асимптоты теоретических кривых

Важное значение в теории количественной интерпретации данных электрических зондирований имеет анализ асимптотического поведения кривых зондирований при больших и малых r.

Для построения асимптот теоретических кривых ρ_к необходимо найти низкочастотную и высокочастотную асимптотики приведенного импедансного отношения .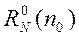

Рассматривают два случая.

сопротивления (0 < ρ_N < ∞).

В случае двуслойного геоэлектрического разреза имеем:

= cth(n₀d₁ + arcth ). (1.32)

Пусть n₀ → 0, тогда получим:

= cth(arcth ) = . (1.33)

В случае трехслойного геоэлектрического разреза имеем:

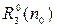= cth(n₀d₁ + arcth( cth(n₀d₂ + arcth())). (1.34)

Пусть n₀ → 0, тогда получим:

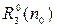= cth arcth( cth arcth()) = = . (1.35)

С помощью метода математической индукции полученные соотношения можно распространить и на N - слойный разрез:

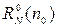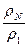~ при n₀ → 0. (1.36)

2. В основании разреза лежит пласт-изолятор (ρ_N = ∞).

Рассмотрим двуслойный разрез.

Так как arcth x = = , (1.37)

Тогда получим: 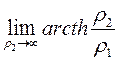= = = 0. (1.38)

Следовательно, в этом случае = cth(n₀d₁). (1.39)

Для гиперболических функций известна следующая асимптотика при x → 0: сth x ~ 1/x.

Тогда формула (1.39) будет иметь вид:

= cth(n₀d₁) ~ 1/n₀d₁ = 1/n₀ρ₁S₁, (1.40)

где S₁ = d₁/ρ₁ – продольная проводимость первого слоя.

Рассмотрим трехслойный разрез.

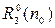= cth(n₀d₁ + arcth( cth n₀d₂)). (1.41)

При n₀ → 0 с учетом (1.40) получим:

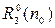= cth(n₀d₁ + arcth(ρ₂/n₀ρ₁d₂)) ~

~ cth(n₀ρ₁d₁/ρ₁ + n₀ρ₁d₂/ρ₂) ~ 1/n₀ρ₁(S₁ + S₂) = 1/n₀ρ₁S, (1.42)

где S = S₁ + S₂ = d₁/ρ₁ + d₂/ρ₂- суммарная продольная проводимость разреза (поскольку только первые два слоя и являются проводящими).

Этот результат при n₀ → 0 обобщается на N - слойный разрез:

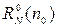= 1/n₀ρ₁S, (1.43)

где S= = 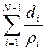- суммарная продольная проводимость разреза.

Вид теоретических кривых зондирования в случае конечного сопротивления основания (0 < ρ_N < ∞) (рис. 2).

Рис. 2.

При больших значениях rкривая кажущихся сопротивлений асимптотически приближается к горизонтальной прямой, отсекающей на оси абсцисс удельное электрическое сопротивление основания разреза ρ_N.

Если в основании разреза лежит пласт-изолятор (ρ_N = ∞), то абсцисса точки пересечения наклонной асимптоты с горизонтальной осью численно равна значению суммарной продольной проводимости S (в См). Указанная наклонная асимптота получила название линии S.

При r → 0 (n₀ → ∞) для любого одномерного разреза будем иметь:

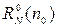= cth(n₀d₀ + ……) ~ 1, (1.44)

где воспользовались формулой:

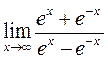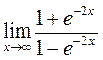= = = 1. (1.45)

Откуда будем иметь:

ρ_к(r) = -ρ₁r² ( 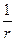) = ρ₁. (1.46)

Таким образом, при изображении кривой зондирования ρ_к на билогарифмическом бланке эта кривая имеет левую горизонтальную асимптоту, отсекающую на вертикальной оси величину ρ₁.

Полученный результат допускает простое физическое истолкование. В самом деле, при маленьких rэлектрическое поле проникает лишь в первый пласт, следовательно, при малых rслоистый разрез можно заменить однородным полупространством с сопротивлением ρ = ρ₁для которого кажущиеся сопротивления совпадают с истинными.

Дата добавления: 2014-11-16