Метод Н. Кано и Е. Имбембо

Металла образованию и распространению трещины

Энергетические методы определения сопротивляемости

Большинство методов, позволяющих определить работу на стадии образования трещины А_з, являются комплексными.

Метод Л. С. Лившица и А. С. Рахманова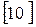

При данном методе испытывается серия надрезанных одинаковых образцов с увеличением энергии удара на каждом последующем образце и определяется угол загиба образца (рис. 4.15). Величину энергии увели-чивают до уровня, при котором появляется трещина. Часть образцов разру-шают полностью, определяя максимальный угол загиба a_max. По результа-там испытаний строится график, из которого можно определить суммар-ную работу до появления трещины (А_упр + А_деф), а также работу на рас-пространение трещины (А_р).

Поглощенная энергия А, Дж

О – неразрушенные образцы; · – полностью разрушенные образцы

Рисунок 4.15 – Схема определения составляющих работы

ударного изгиба

По диаграмме растяжения определяется работа до появления трещи-ны и работа, затрачиваемая на распространение трещины в образце (рис. 4.16) [10 ].

Рисунок 4.16 – Форма и размер образца Н.Кано и Е.Имбембо

Распределение работы на составляющие возможно также при испо-льзовании образцов с разными радиусами надреза (методы А.П.Гуляева и В.С.Ивановой).

Метод А. П. Гуляева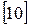

По данному методу серия образцов с разными радиусами надреза (рис.4.17) испытывается на ударный изгиб.

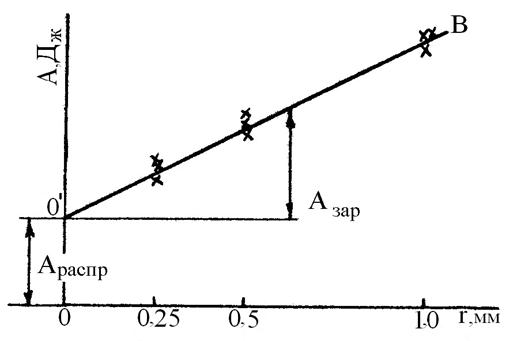
Рисунок 4.17 – Обработка результатов испытаний надрезанных

образцов на ударный изгиб

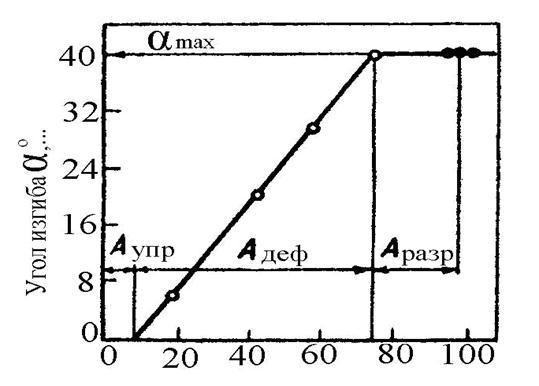
По результатам испытаний, при которых регистрируется полная ра-бота А, поглощенная образцом при разрушении, проводится прямая О'В и определяется:

А_зар - работа, идущая на изгиб образца до появления трещины.

А_распр - работа, идущая на распространение трещины в образце.

Метод В.С.Ивановой

Строится график (рис.4.18) зависимости ударной вязкости не от ра-диуса надреза r, а от величины 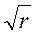. Предполагается, что при некотором малом радиусе надреза работа изгиба образца становится крайне малой и вся энергия тратится на распространение трещины. Отрезок по оси орди-нат между горизонтальным и наклонным участками ломаной линии выра-жает работу образования трещины А_з, зависящую от геометрии надреза.

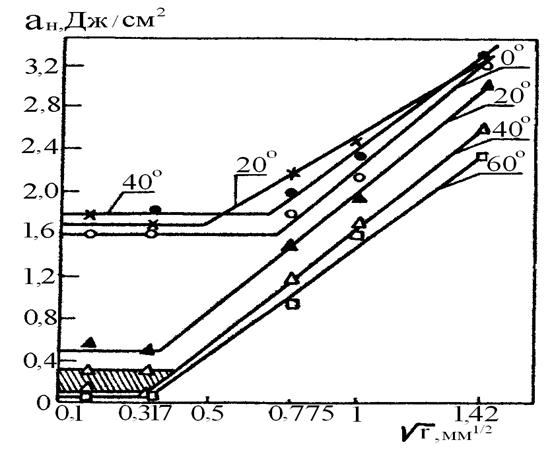
5, ○ – острый надрез; ●, х – по радиусу надреза

Рисунок 4.18 – Распределение ударной вязкости на составляющие для стали 15Г2 при разных отрицательных температурах испытания

4.8 Силовые критерии разрушения

Разрушение материалов вследствие развития трещины и сосредото-ченное в маленьком круге вершины трещины, где очень высокая концен-трация напряжений, обусловлено малым радиусом закругления. Напря-женное состояние в этой зоне, пользуясь методами теории упругости, можно в общем виде выразить формулой

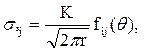(4.29)

где К – коэффициент интенсивности напряжений;

і, j = х, у – координатные оси;

f _{і, j} – зависимость 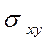от угла .

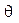Коэффициент К зависит от вида нагружения, величины напряжения, формы трещины. В зависимости от вида нагружения (см. рис.4.9) он обоз-начается соответственно индексами I,II, III, то есть, К_I, К_II, К_III.

При деформации растяжения (см.рис.4.9,а) при плоском напряжен-ном состоянии формула напряжения (4.29) имеет вид:

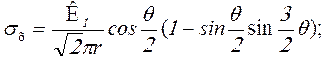(4.30)

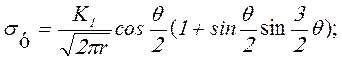(4.31)

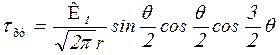. (4.32)

Перемещения U и V в направлении осей Х и У (рис. 4.19) соответ-ственно определяются по формулам:

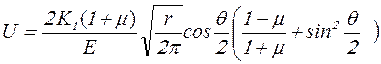; (4.33)

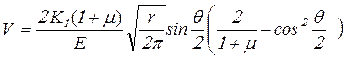. (4.34)

Коэффициент интенсивности напряжений возле вершины трещины при плоской деформации имеет вид

К₁ 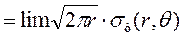; (4.35)

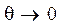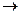; r 0.

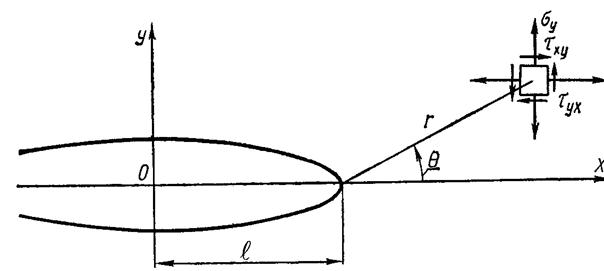
Рисунок 4.19 – Полярные координаты r и q _з с полюсом в вершине трещины

При растяжении пластины с трещиной длиной 2 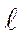по схеме рис.4.19 нормальные напряжения в сечении пластины вокруг трещины будут равны:

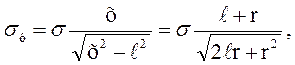(4.36)

где х – координата, отсчитываемая от середины трещины,

тогда r = х - .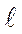

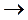
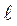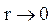Около вершины трещины, при х и , напряжения неогра-

ниченно растут по модулю. Подставляя уравнение для σ_у (4.36) в урав-нение для вычисления К₁ (4.35) и вычисляя, находим:

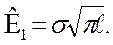(4.37)

Для пластин ограниченных размеров при разных видах нагружения и расположения трещин критическое значение коэффициента интенсив- ности напряжений определяется по формуле

(4.38)

где f_1кр – поправочные коэффициенты, которые приведены в спра-вочной литературе и в таблице 4.1.

Таблица 4.1 – Выражения для f_1кр[5]

Вид нагружения и расположения трещины	Схема	Поправочная функция
Растяжение неог-раниченной пласти-ны с наклонной тре-щиной в середине		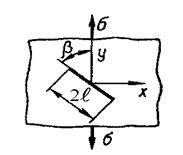f1кр = sin^2β
Растяжение полу-бесконечной плас-тины с односто-ронней трещиной		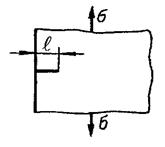f1кр = 1,12
Растяжение пласти-ны шириной 2В с поперечной трещи-ной посередине		f1кр=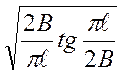
Растяжение пласти-ны шириной 2В с двумя боковыми трещинами		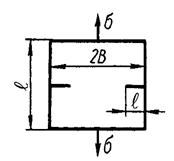f1кр=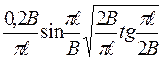
Продолжение таблицы 4.1
Изгиб в плоскости пластины шириной В и толщиной Н с попе-речной трещиной по-середине		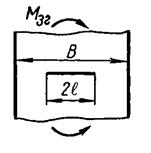f1кр=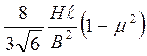
Действие внутренне-го давления р на ци-линдрическую трубу диаметром 2R и тол-щиной Н при продоль-ной сквозной трещине		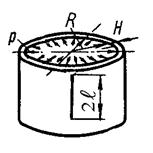f1кр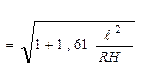

В линейной механике разрушения выходят из предположения, что трещина распространяется тогда, когда коэффициент интенсивности нап-ряжений и интенсивность высвобождаемой энергии достигают критичес-кого значения, характерного для данного материала, тогда критерий развития трещины для нормального отрыва имеет вид: К₁ = К_1с и G₁ = G_1с.

Для плоского напряженного состояния высвобождаемая энергия обозначается G₁и равняется:

,

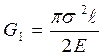адля условий плоской деформации

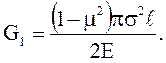
Таким образом имеем две эквивалентные формулировки критерия разрушения:

1) энергетическая, согласно которой допускается, что трещина мо-жет распространяться тогда, когда интенсивность высвобождаемой эне-ргии G достигает критического значения:

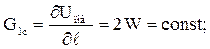
2) силовая, согласно которой трещина может распространяться при достижении коэффициентом интенсивности напряжений К своего кри - тического значения:

К_с = const.

Энергетический критерий является необходимым условием распрос-транения трещины, но он не обязательно должен быть достаточным. Если материал при вершине трещины не находится на грани разрушения, то тре- щина не будет расти даже при достаточной энергии для её развития. Мате-риал должен до конца исчерпать свою способность воспринимать нагрузки и продолжать деформироваться, то есть силовой критерий должен быть эквивалентным энергетическому, между которыми существует зависи-мость:

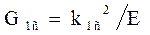– плоское напряженное состояние;

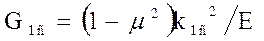– плоская деформация.

С помощью этих соотношений можно рассчитать предельное состо-яние элементов конструкций с трещиной, а также оценить механические свойства материала и его способность тормозить развитие трещины.

Дата добавления: 2014-11-16