Определение размера пластической деформации

в области вершины трещины

В толстых пластинах с трещиной около её вершины возникает плос-кое деформированное состояние, а в тонких – плоское напряженное состо-яние, при котором размер пластической зоны у конца трещины больше, чем в толстом металле. Величина К_1с в качестве критерия стойкости тре-щины может быть справедливой только для достаточно толстых пластин, где пластическая зона около вершины трещины мала.

Д. Ирвиным было показано, что наличие пластической зоны можно учесть, если вместо длины физической трещины 2 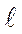в расчетах использо-вать эффективную длину 2 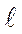_эф = 2 ( 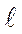+ а), где а – поправка на пластич-ность. Её можно определить по рис.4.20, на котором по всей длине зоны пластичности r_р = а + b напряжения σ_у приняты равными σ_Т. Кривая упругих напряжений σ_у меняется по закону σ_у = .

Рисунок 4.20 – Схема определения пластической зоны вдоль трещины

Площадь под пунктирной кривой σ_у равна площади прямоугольной эпюры на длине (а + b)σ_Т, а напряжения σ_у равны пределу текучести σ_Т при r = b, то есть σ_Т. Из двух уравнений находим:

r = а = b = (4.39)

Из рис. 4.21 следует, что напряжение σ_у = , возникающее не-посредственно перед трещиной, будет превышать σ_Т на некотором рассто-янии r от вершины трещины, то есть r ограничивает зону упругого напря-жения. Принимая, что на границе между упругой и пластической зоной 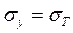, получим: и размер зоны пластической деформа-ции оказывается равным 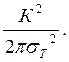Наличие зоны пластической деформации определяет как бы увеличение длины трещины по сравнению с её “дейст-вительной “длиной.

Рисунок 4.21 – Оценка размера зоны пластичности

Энергетический критерий для нестабильного развития трещины длиной 2 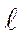имеет вид

(4.40)

где W_кр – критическая энергия деформации, необходимая для об-разования свободной поверхности трещины при наличии пластичес-ких деформаций.

Выражение для коэффициента интенсивности напряжений К₁ с уче-том решения для σ_у позволяет приближенно определить длину пласти-ческой зоны r_т вдоль трещины. Так, при σ_у = σ_т для плоского напряжен-ного состояния в пластине неограниченных размеров

(4.41)

или с учетом выражения :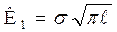

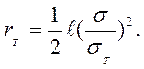(4.42)

Для пластины ограниченной ширины

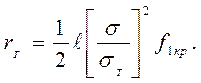(4.43)

Тогда половина длины трещины с учетом пластической зоны

(рис. 4.22):

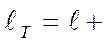r_Т = 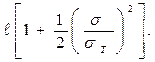(4.44)

Рисунок 4.22 – Схема раскрытия трещины

Пользуясь величиной 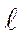_т, по приведенным выше формулам мож-но определить К_1с, а затем и перемещение V возле вершины трещины. Для плоского напряженного состояния при r = r_т,

(4.45)

Удвоенная величина V равняется раскрытию трещины d:

(4.46)

В случае хрупкого разрушения при σ < σ_т раскрытие трещины приближенно можно найти по формуле

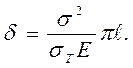(4.47)

Результаты определения раскрытия трещины по формуле (4.47) при

σ 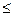σ_т подтверждаются экспериментально.

При плоском деформированном состоянии вследствие того, что зна-чения d и r меньше, длина пластической зоны уменьшается в несколько раз в сравнении с такой же при плоском напряженном состоянии.

С учетом размера зоны пластической деформации в пластине с коэф-фициентом интенсивности напряжений К коэффициент интенсивности напряжений К_эф определяется по уравнению, включающему эффективную длину трещины

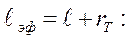(4.48)

К _эф = = (4.49)

где - половина длины трещины.

Коэффициент К_эф всегда больше К_, но в условиях низких напряже-ний разница может быть небольшой. Размеры пластической зоны возле вершины трещины для одного и того же материала зависят от степени деформации вдоль переднего края трещины. Степень сжатия деформа-ции зависит от толщины образца S (рис.4.23), с увеличением которой напряженное состояние изменяется от плоского напряженного, при кото-ром = 0, до объемного при плоской деформации, когда

σ_z = μ(σ_х + σ_у).

Разрушение одного и того же металла в условиях плоского напря-женного состояния и в условиях плоской деформации разное. В условиях плоской деформации утонение металла невозможно (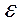 _z = 0), остаточная полная деформация вдоль трещины 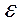_х также равняется нулю, то есть остаточная деформация 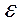_у может находиться в пределах упругих де-формаций.

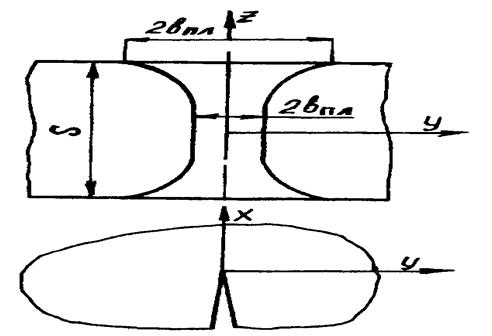
Рисунок 4.23 – Схема распределения пластических деформаций по

толщине элемента

Во время плоской деформации затраты энергии на пластическую деформацию создают разрушающие деформации γ_ху, которые определя-ют размер зоны пластической деформации в_пл На поверхности листа, где существует плоское напряженное состояние, зона пластических деформа-ций 2в_пл существенно больше (см.рис.4.23). Между зоной на глубине, работающей при плоской деформации, и зонами на поверхностях воз-никают значительные касательные напряжения τ_zx и τ_zу, которые не поз-воляют поверхностным зонам деформироваться независимо от зоны в глубине. Размер зоны пластических деформаций возрастает при посте-пенном утончении металла приблизительно до толщины S и равняется сумме двух размеров губ среза. При этом на боковой поверхности плос-кого образца при условии отсутствия внешнего давления всегда имеет место плоское напряженное состояние, поэтому размеры пластической зоны возле свободной поверхности образца всегда больше, чем в сред-ней части (рис. 4.24).

Поскольку в средней части образца имеет место объемное напря-женное состояние, то сопротивление разрушению в этой зоне будет ме-ньшим, а поэтому и фронт продвижения трещины будет выдаваться впе-ред.

Рисунок 4.24 – Форма пластической зоны впереди вершины трещины

в толстом плоском образце

Для образцов разной толщины соотношение пластических зон впе-реди трещины разное, в связи с чем изменяется значение энергии, затра-ченной на разрушение. Существует следующая зависимость характерис-тики трещиностойкости – коэффициента интенсивности напряжений К_с от толщины образца:

(4.50)

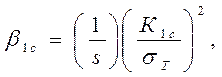(4.51)

где К_с – коэффициент интенсивности напряжений для плоского на-пряженного состояния;

К_1с – коэффициент интенсивности напряжений для плоской де-формации;

β_1с – коэффициент, учитывающий переход от К_с до К_1с в зависи-мости от толщины;

s – толщина металла.

На рисунке 4.25 приведена графическая зависимость К от толщины металла.

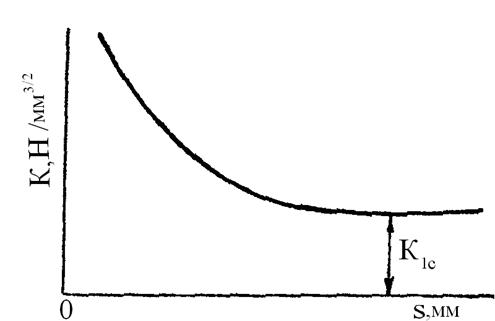
Рисунок 4.25 – Зависимость К от толщины металла

Из рисунка видно, что с увеличением толщины металла наблюдается переход от плоского напряженного состояния к плоской деформации.

Дата добавления: 2014-11-16