Решение. Принимая, что пластина неограниченно большая, размер пласти-ческой зоны rТ определим из уравнения rТ =

Принимая, что пластина неограниченно большая, размер пласти-ческой зоны r_Т определим из уравнения r_Т =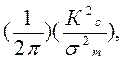

где К_с= 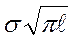, а 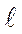= ½ длины трещины.

r_Т =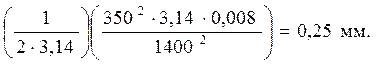

В связи с тем, что величина отношения r_т / 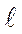очень мала

(0,25/16 = 0,015), то К_эф согласно зависимости (4.50) не будет существен-но превышать К_с (на 2%).

К_эф=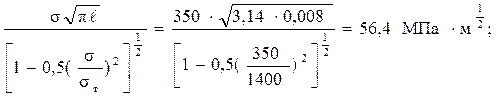

К_с =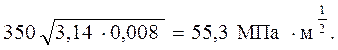

После термической обработки пластины размер пластической деформации составит:

r_Т =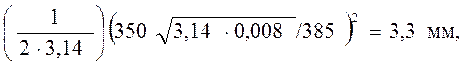

то есть размер зоны пластической деформации составит уже 1/5 от пол-ной длины трещины, а эффективный коэффициент интенсивности напря-жений будет значительно больше (на 28,4%).

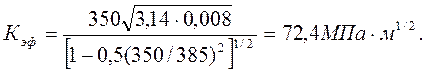
Пример 2 . Пластина из сплава с пределом текучести σ_т =

= 415 МПа имеет значение коэффициента интенсивности напряжения К_1с= =132 МПа· м^1/2, которое определено для толщины S =250мм. Необходимо определить для широкой пластины толщиной 100мм, на какую величину сможет подрасти трещина от отверстия в центре пластины к началу раз-рушения при действующем на пластину напряжении σ_д = 100 МПа.

Решение

Будет неверно использовать уравнение К_с = σ 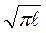и подставить в не-

го значение К_1с = 132 МПа·м^1/2 , так как толщина пластины 100 мм будет занимать промежуточное положение между плоской деформацией и плоским напряженным состоянием. Но значение К_с можно определить, если использовать эмпирическое соотношение К_с² = К²_1с(1 + 1,4 β²_1с),

где β_1с = (1/S)(К_1с/σ_т)²;

S – толщина пластины.

β_1с = (1/0,1)(132/415)² = 1,01;

К²_с = 132² (1+1,4·1,01) = 41817,6 МПа·м^1/2, К_с = 204,5 МПа·м^1/2.

Находим критическую длину трещины для толщины пластины 250 мм:

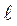₁= К²_1с /σ²_д ·π = 132² / 100² ·3,14 = 0,55м,

где 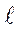₁– половина длины трещины, а полная длина будет равняться 1,1м.

Для металла толщиной 100 мм половина критической длины трещи-ны будет равняться:

= К²_с /σ²_д π = 204,52/ 100² ·3,14 = 1,33 м, а полная длина -

2,66 м. То есть трещина для пластины толщиной 100 мм может возрасти на 2,66 –1,1 = 1,56 м.

Пример 3 . Определить запас прочности цилиндрического сосуда диаметром D = 480 мм и толщиной стенки H = 8,5мм, работающего в условиях комнатной температуры под внутренним давлением Р = 28 МПа и в котором при обследовании была выявлена с внутренней стороны полу-

эллиптическая трещина глубиной = 3мм и длиной вдоль образующей

2 а = 8,5 мм (рис.4.30, а). Материал сосуда - сталь (предел текучести

σ_Т = 1000 МПа; предел прочности σ_В =1200 МПа).

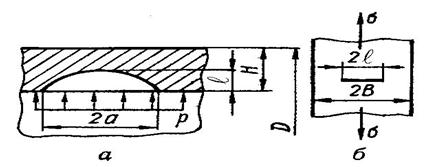
Рисунок 4.30

Решение

Для определения характеристики трещиностойкости стали было проведено испытание соответствующих образцов в условиях комнатной температуры при статическом нагружении по схеме рис.4.30, б. Образцы шириной 2 В и толщиной, равной толщине стенки сосуда (8,5мм), имели центрально расположенную трещину длиной 2 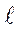= 10мм. Номинальное напряжение, при котором образцы разрушались по минимальному сече-нию, равнялось σ_н = 720 МПа. Результаты испытаний показали, что при выбранной толщине образца его материал находился в хрупком состоянии, а запас прочности в данном случае можно рассчитать, используя теорию линейной механики разрушения. Поэтому критическое значение коэффи-циента интенсивности напряжений К_1с можно найти, воспользовавшись формулой

К_1с = f_1крσ_кр ,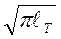

где f_1кр – поправочный коэффициент, учитывающий схему нагруже-ния, тип, размеры образца и характер трещины;

σ_кр – номинальное разрушающее напряжение в неослабленном сечении;

_Т – длина трещины с учетом пластической деформации у её вершины.

Напряжение σ_кр определим через номинальное напряжение в ослаб- ленном сечении:

σ_кр = .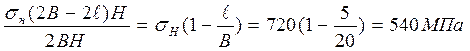

Условная длина трещины _Т с учетом формулы (4.44)

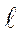_Т =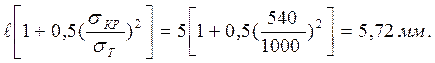

Поправочный коэффициент

f_1кр =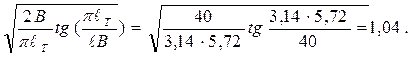

Тогда К_1с = f_1крσ_кр =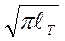

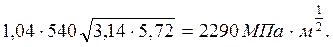
Этот коэффициент используем для определения номинального раз- рушающего напряжения в сосуде для заданной выше трещины. Номина- льное главное напряжение в стенке сосуда (принимаем его тонкостенным) старается разрушить сосуд по образующей. Согласно формуле Лапласа оно равно:

σ_1н =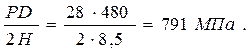

Коэффициент интенсивности напряжений К_1с для рассматриваемой трещины, согласно формуле (4.40), без учета пластической деформации равен:

К_1с = f_1крσ_1кр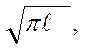

где σ_1кр – критическое разрушающее напряжение для сосуда;

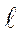- половина глубины трещины.

Поправочный коэффициент для несквозной полуэллиптической по-верхностной трещины глубиной 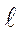(малая полуось) и длиной на поверх-ности 2 а(а - большая полуось) в пластине толщиной H находим из зависи-мости

f_1кр 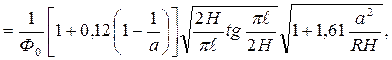(4.55)

где Ф₀ – величина, зависящая от соотношения 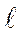/ а (при увели-чении 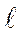/ а от 0,1 до 1 Ф₀ равномерно увеличивается от 1 до π /2).

При 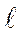/ а = 3 /4,25 = 0,71 это соотношение составляет 1,39. Тогда, подставляя в формулу (4.50) искомые величины, найдем:

f_1кр .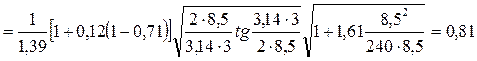

Критическое напряжение для сосуда

σ_1кр =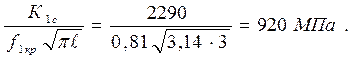

Глубина трещины с учетом пластической деформации, которая воз-никла в её вершине, согласно формуле (4.44)

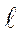_Т =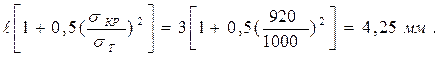

Предполагая, что размер трещины 2 а растет пропорционально, нахо-дим:

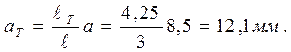
Поправочный коэффициент f_1кр согласно формуле (4.55), составит:

f_1кр .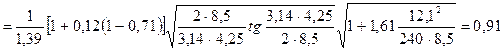

Тогда значение уточненного разрушающего напряжения с учетом пластической деформации 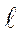_Т = 4,25мм и f_1кр= 0,91 составит:

σ_1кр =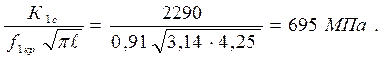

Для определения разрушающего напряжения σ_1кр во втором прибли-жении необходимо в формуле (4.44) учесть уточненные размеры трещины:

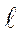_Т =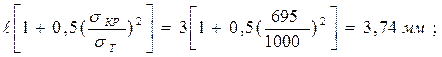

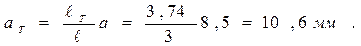
Тогда поправочный коэффициент f_1кр согласно формуле (4.55)

f_1кр .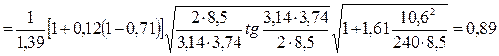

Разрушающее напряжение во втором приближении

σ_1кр =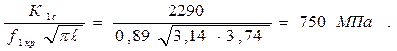

Дальнейшее приближение не даёт существенного уточнения. Таким образом, полученное критическое напряжение σ_1кр по сравнению с номи- нальным напряжением у стенки σ_1н дает возможность определить запас прочности стенки сосуда с трещиной:

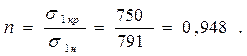
Так как n < 1, то эксплуатация сосуда с данным дефектом недопус-тима.

5 ВЛИЯНИЕ ДЕФЕКТОВ НА РАБОТОСПОБНОСТЬ

СВАРНЫХ КОНСТРУКЦИЙ

Современный уровень технологии производства сварных конструк- ций не позволяет избежать появления дефектов. Их влияние и исправление осуществляют в соответствии с рекомендациями отраслевых нормативно-технологических документов, устанавливающих характер и размеры де- фектов, подлежащих исправлению. Эти документы ориентируются на дос- тигнутый в каждой отрасли уровень техники, технологии сварки и контро-ля качества. Однако такой подход неприемлем при ускоренных темпах внедрения новых материалов и способов сварки.

Отсутствие учета функциональной связи “ размер дефекта – условия работы” при установлении норм приводит к необоснованным требованиям исправления дефектов, не уменьшающих несущую способность конструк- ции или, наоборот, допуску таких, которые могут привести к эксплуатаци-онному отказу. При заварке дефектных мест возможно образование новых дефектов, даже более опасных, чем исправляемые.

Формирование сварных соединений в процессе сварки происходит под влиянием большого количества факторов. Форма, размеры, поверхнос-ти сварных швов всегда имеют отклонения от проектных. Радиусы сопря- жений швов с основным металлом колеблются в широких пределах. Вза-имное расположение соединяемых элементов также может отличаться от проектного из-за смещений и угловых поворотов. Сплошность металла сварных соединений в некоторых случаях нарушается из-за появления пор, шлаковых включений, пленок оксидов, несплавления шва с основным металлом, трещин, надрезов, наплывов и др. Подобные отклонения на практике оказываются неизбежными и оказывают влияние на механичес-кие свойства сварных соединений. Степень влияния различных отклоне-ний в разных условиях эксплуатации будет разной. Поэтому не всякие от-клонения и не всегда можно отнести к дефектам сварных соединений. Де-фектами считают такие, которые имеют недопустимые отклонения от уста-новленных норм. Нормы, в соответствии с которыми отклонения относят к дефектам и браку, должны, в первую очередь, устанавливаться на основе изучения их влияния на прочность и другие эксплуатационные свойства сварных соединений.

5.1 Проблема учета влияния дефектов на работоспособность

сварных соединений

Проблема влияния дефектов на прочность сварных соединений край-не сложна и многопланова. Решить ее можно, учитывая условия эксплуа-тации, характер дефекта и свойства металла сварного соединения. Иссле-дования в области влияния дефектов на прочность группируются вокруг отдельных вопросов. В особые направления выделяются вопросы: а) влия-ния дефектов при переменных нагрузках, в условиях коррозии, при низких и высоких температурах и т.д.; б) влияния трещин, непроваров, пор, сдви-гов, мест перехода от наплавленного металла к основному и т.д. в зависи-мости от вида дефекта; в) исследования разных материалов: высокопроч-ных сталей, алюминиевых и титановых сплавов.

В связи с таким многообразием проблем в данном курсе рассматри- ваются только наиболее принципиальные вопросы чувствительности ме-талла к концентрации напряжений, а именно – при наличии трещин, как наиболее опасных дефектов, при статических и динамических нагрузках.

5.2 Оценка влияния трещиноподобных дефектов по силовым и

деформационным критериям. Влияние толщины металла

При статических нагрузках вопрос о влиянии дефектов на прочность в большинстве случаев сводится к вопросу о чувствительности металла к концентрации напряжений. При этом наметились два направления в оцен-ке чувствительности – на базе аппарата линейной механики разрушения относительно трещин и трещиноподобных дефектов и на базе теории кон-центрации напряжений.

Под действием статической нагрузки при наличии трещин в качестве меры чувствительности (нечувствительности) к концентрации напряжений в условиях плоской деформации (как наиболее напряженному состоянию) используется критический коэффициент интенсивности напряжений ме- талла К_1c. Чем он выше, тем менее чувствителен металл к концентрации напряжений. Однако при другой температуре эксплуатации тот же самый металл может оказаться чувствительным к концентрации напряжений. Так как каждый металл имеет определенный уровень прочности (s_т и s_в) и обычно предназначен для работы при напряжениях, несколько меньших s_т, то оценку нечувствительности в присутствии трещин более точно можно дать по отношению К_1c/s_т. Эту величину можно рассматривать как пропорциональную корню квадратному из длины трещины в бесконечной пластине, при которой среднее разрушающее напряжение равняется σ_т. Тогда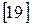

К_1c/s_т 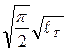= s_т /s_т = 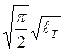, (5.1)

где _т – длина трещины, вызывающая разрушение металла при

s = s_т.

Для высокопрочных сталей размер 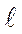_т составляет миллиметры или десятые доли миллиметра (эти стали крайне чувствительны к наличию тре-щин); низколегированные стали невысокой прочности при комнатной тем-пературе имеют 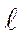_т, измеряемое десятками миллиметров, то есть, чувст-вительность этих сталей к концентрации напряжений различается более чем в 10 раз.

Однако не всегда толщина металла достаточна, чтобы были созданы условия плоской деформации. Но отход от плоской деформации не означа- ет переход к плоскому напряженному состоянию. В условиях неплоской деформации существует широкая гамма промежуточных напряженных состояний.

Толщина пластины существенно влияет на напряженно – деформи - рованное состояние при вершине трещины. Для определения вязкости раз - рушения материала К_1с для условия плоской деформации необходим толс-тый образец в зависимости от соотношения (К_1c/s_т)². В тонких образцах размер зоны пластичности не маленький в сравнении с толщиной и у них возникает плоское напряженное состояние. Существует оптимальная тол - щина в_о, при которой вязкость достигает своего максимального значения, которое обычно полагают равным действительной вязкости разрушения при плоском напряженном состоянии (рис.5.1). В переходной области ме –

жду в_о и в_s вязкость приобретает промежуточное значение .

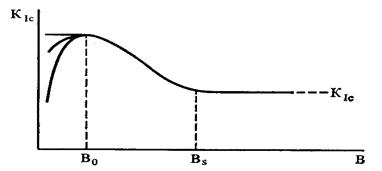
Рисунок 5.1 – Ударная вязкость как функция толщины

Рассмотрим четыре панели с толщинами В₁, В₂, В_3, В₄ (рис.5.2).

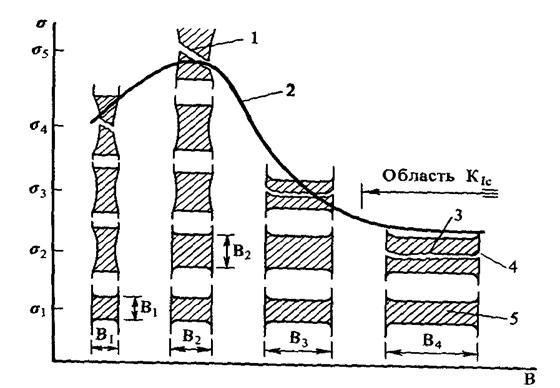
1 – косое разрушение;

2 – зависимость остаточной прочности панелей с трещинами от толщины;

3 – плоское разрушение; 4 – губы сдвига; 5 – пластическая зона

Рисунок 5.2 – Остаточная прочность как функция толщины

Все панели имеют одинаковую длину трещины и нагружены оди-наковым напряжением σ₁: интенсивности напряжений во всех панелях одинаковые, то есть зоны пластичности в панелях имеют одинаковые размеры. На рис. 5.2 показаны поперечные сечения четырех образцов.

Зоны пластичности, соответствующие напряжению σ₁, заштрихова-

ны. В панелях В₂, В₃, В₄ вертикальные размеры зоны пластичности ме-ньше толщины, поэтому в них не может развиваться свободная текучесть в направлении толщины пластины; этот процесс сдерживается упругим ма-териалом. Таким образом, деформация в направлении толщины пластины остается равной нулю, то есть имеем плоское деформированное состоя-ние. В панели В₁ размер зоны пластичности равен толщине и текучесть в направлении толщины ничем не ограничивается. Это означает, что в пане-ли В₁ может полностью развиваться плоское напряженное состояние и из этого момента зона пластичности в панели В₁ будет больше, чем в других панелях.

Увеличение напряжения до величины σ₂ приведет к разрушению па-нели В₄, так как в ней возникнут достаточные для этого напряжения и де-формации. Панель В₃ находится в тех же условиях, что и панель В₄, и в ней, вероятно, произойдёт некоторое распространение трещины. Однако из-за влияния областей с плоским напряженным состоянием (малым нап- ряжением при вершине трещины), которые расположены вблизи поверх-ности образца и которые в этой более тонкой панели имеют сравнительно большее влияние, сама панель еще не разрушится. Панель В₂ находится в подобных условиях, однако толщина ее теперь равна размеру зоны плас-тичности. Это означает, что в ней возникает плоское напряженное состо- яние.

Дальнейшее увеличение напряжения приведет к разрушению при на- пряжении σ₃ панели В₃. При напряжении σ₄ деформации при вершине тре-щины панели В₁ станут настолько большими, что состоится ее разруше-ние. Однако панель В₂ не разрушится, так как с того момента, как напря-жение достигло величины σ₁, деформации в панели В₂ были меньше, чем деформации в панели В₁. Поэтому деформации в панели В₂ еще недоста-точны для разрушения, несмотря на то, что напряжения в ней приблизите-льно такие же, как и в панели В₁. Для разрушения панели В₂ необходимо дальнейшее увеличение напряжения до величины σ_5. Панели с толщиной, большей В₄, разрушаются при том же напряжении σ₁, что и панель В₄. Здесь лежит область разрушений при плоском деформированном состоя-нии. В более тонких панелях В₁ образуются большие деформации и разру-шения происходят при более низких внешних напряжениях σ_4.

Таким образом, чем меньше толщина проката из того же самого ме- талла, тем менее чувствителен он к концентрации напряжений, то есть его разрушение при одной и той же длине, сквозной или относительной глуби-не непроходной трещины будет происходить при более высоких напряже-ниях. Таким образом, толщина в металле является фактором, который не относится к свойствам металла, но влияет на его чувствительность к нали-чию трещин.

При сквозных трещинах нечувствительность металла конкретной толщины к концентрации напряжений в условиях неплоской деформации оценивается также отношением Кс_т/s_т. При этом Кс_т – наименьшие при рассеянии значения критического коэффициента интенсивности напряже-ний металла К_с, которые определены при напряжениях, меньших s_т. Это означает, что из серии значений К_с, найденных и при s > s_т, Кс_т – макси-мальное, которое может быть вообще воспринято металлом данной тол-щины без разрушения при наличии сквозной трещины. Трактовка

К_cт/s_т =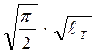

остается такой же самой, что и для формулы (5.1).

Вид поверхностей разрушения образцов по толщине s приведен на рис. 5.4. Критерии механики разрушения могут быть применены также и для непроходных (несквозных) трещин, распространяющихся от поверх- ности (рис.5.3).

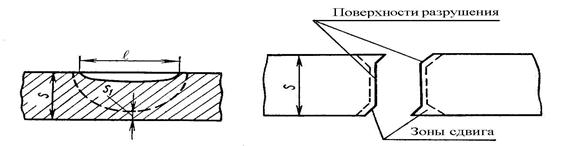
Рисунок 5.3 – Поверхностная Рисунок 5.4 – Вид поверхностей

трещина в металле толщиной s разрушения образца из металла

толщиной s

Эти трещины при увеличении напряжения (нагрузки) растут преиму- щественно в направлении толщины, мало увеличиваясь по длине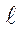

(см. рис.5.3). Даже при небольших толщинах s на большей части криволи-нейного фронта трещины обеспечиваются условиями плоской деформа-ции, так как небольшие трещины могут стать критическими. При прибли-жении фронта трещины к противоположной поверхности на участке s₁, разном по размерам у разных металлов, возникают условия деформирова-ния металла, близкого к плоскому напряженному состоянию, которое про-является в повышенной пластической деформации металла перед разру-шением. Для вычисления К в зависимости от уровня напряжений и формы трещины имеются соответствующие формулы, которые приведены в спе-циальной литературе. При поверхностных (несквозных) трещинах оценка нечувствительности металла к концентрации напряжений для деталей бо-льшого сечения также проводится по соотношению К_ст/s_Т, так как условия плоской деформации здесь могут быть реализованы полностью. При ма-лых толщинах оценка по К_ст /s_т, то есть по силовому критерию, приведет к абсурду, так как при s_кр>s _т значения К_с будут выходить тем меньшими, чем тоньше металл. Для сохранения единства подхода к оценке чувстви-тельности листового металла любой толщины к концентрации напряжений как чувствительных, так и нечувствительных материалов при s_кр > s_т не-обходимо переходить к деформационному критерию механики разрушения V_p и давать оценку по отношению

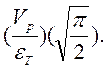(5.2)

При s_кр< s_т оценку можно давать как по К_с, так и по V_p, так как результаты будут выходить одинаковыми. Вычисления V_р при s_кр > s_т выполняются по тем же формулам, что и К_с, но вместо среднего расчетно-го напряжения в ослабленном сечении образца берется средняя деформа-ция 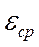. Имея металлы с разными свойствами и разной толщины, можно расположить их по критерию К_ст/s_т или (V_p / 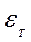) () 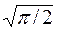в ряд нечувст-вительности к концентрации напряжений. Однако следует иметь в виду, что тот же самый металл разной толщины будет иметь разную чувстви-тельность к сквозной трещине, но может иметь одинаковую чувствитель-ность к несквозной трещине. В образцах с несквозной трещиной при оди-наковой чувствительности и одинаковой относительной глубине трещины металл меньшей толщины будет разрушаться при более высоких напряже-ниях и деформациях, чем тот же металл большей толщины, так как на ма-ленькой толщине невозможно иметь трещину более глубокую, чем толщи-на металла.

Дата добавления: 2014-11-16