Ход работы. Тема: Построение графика линейной функции по результатам эксперимента (с использованием уравнения линейной регрессии)

Тема: Построение графика линейной функции по результатам эксперимента (с использованием уравнения линейной регрессии).

Лабораторная работа №1.

ПРИМЕРЫ ОБРАБОТКИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ И ВАРИАНТЫ ЗАДАНИЙ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

ЛУГАНСК 2007

К практическим работам по дисциплине

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

“Метрология и основы измерений”

(электронное издание)

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

ВОСТОЧНОУКРАИНСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ

имени ВЛАДИМИРА ДАЛЯ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к практическим занятиям по дисциплине
“Метрология и основы измерений”

для студентов направлений подготовки 6.050101 – компьютерные науки, 6.050201- системная инженерия и 6. 050202 – автоматизация и компьютерно – интегрированные технологии
дневной и заочной форм обучения

(электронное издание)

Утверждено

на заседании кафедры

системной инженерии

протокол № 1 от 30.08.07

ЛУГАНСК 2007

УДК

Методические указания к практическим работам по дисциплине “Метрология и основы измерений” (для студентов направлений подготовки6.050101 – компьютерные науки, 6.050201- системная инженерия и 6.050202 – автоматизация и компьютерно – интегрированные технологии дневной и заочной форм обучения) / Сост. А.И. Горбунов, П.Ю. Войлов. - Луганск: Изд. ВНУ им. В. Даля, 2007. - 32 с.

Рассматриваются наиболее часто встречающиеся в практической деятельности задачи и их решения, связанные с обработкой результатов одноразовых и многоразовых прямых измерений, а также с обработкой результатов косвенных измерений. Уделено внимание методике определения параметров, характеризующих абсолютные и относительные погрешности. Решение задач рассмотрено в объеме читаемого теоретического курса «Метрология и основы измерений».

Составители А.И.Горбунов, доц., П.Ю. Войлов, ас.

Отв. за випуск А.И. Горбунов

Рецензент Д.А.Зубов, д.т.н., доц.

Проведение практических занятий и выполнение индивидуальных заданий наряду с лекционным курсом позволяет расширить и закрепить как теоретические знания, так и овладеть практическими навыками обработки результатов измерений и определения параметров их погрешностей.

Каждому индивидуальному заданию предшествует краткая теоретическая информация по теме, излагается ход решения задачи и приводятся применяемые аналитические выражения. Затем приведен пример решения аналогичной задачи с подробными комментариями хода решения. Результаты выполнения индивидуальных заданий могут оформляться в виде отчета как в рукописном варианте в обычной ученической тетради, так и с использованием компьютерного набора на формате А4 в соответствии с требованиями ЕСКД при помощи текстового редактора “Word”.

1. В соответствии со схемой эксперимента (Рис. 1.1) к источнику напряжения U₀ в режиме делителя напряжения подключен переменный резистор R1. Путем изменения положения движка резистора R1 задается ряд значений величин напряжения U_i и тока I_i на нагрузочном резисторе R_Х, которые измеряются вольтметром V и амперметром А соответственно. Считать, что сопротивление амперметра R_A = 0.

Выходные данные для вычислений необходимо свести в таблицу 1.

Таблица 1

i	Ui,B	Ii,A
	U1	I1
	U2	I2
…	…	…
n	Un	In

Известно, что если экспериментально получена совокупность значений x_i, и y_i, причем характер функциональной связи между ними 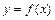теоретически известен, то обработка таких результатов измерений сводится к вычислению параметров функции, наилучшим образом отображающей данную экспериментальную зависимость (такую функцию называют уравнением регрессии).

Этот метод особенно удобно использовать для обработки экспериментальных функциональных зависимостей в случае линейной связи между x и y. Уравнение регрессии имеет общий вид:

.

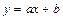В отдельном случае, когда известно, что график уравнения линейной регрессии проходит через нуль координатной системы, это уравнение имеет вид:

(1.1)

Коэффициент а в этом случае вычисляется по формуле:

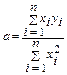; (1.2)

где n - количество пар величин x_i и y_i в данном эксперименте.

Для оценки точности обработки результатов измерений необходимо вычислить среднеквадратическое значение отклонения экспериментальных точек x_i, y_i от уравнения линейной регрессии; ширина полосы, характеризирующая неточность результата равна 2 S_y(x). Среднеквадратическое отклонение вычисляется по формуле:

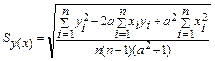. (1.3)

1. Построить в системе координат IOU экспериментальные точки и расчетный график уравнения линейной регрессии Показать экспериментальные точки.

3. Из закона Ома следует:

. (1.4)

В нашем случае уравнения линейной регрессии в общем виде выглядит как: 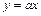. В тоже время, измеряемые в процессе эксперимента величины I и U, связаны функциональной зависимостью: . Если принять: , тогда:

(1.5)

Из формул (1.4) и (1.5) следует: 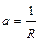. Откуда находим неизвестное сопротивление R_Х:

R_Х = 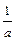. (1.6)

4. В выводе сделать заключение о близости расчетной прямой к эмпирическим данным.

Пример решения:

1. Выходные данные, полученные в результате эксперимента, схема которого приведена на рис.1, сведены в табл.1.

2.

Таблица 1.

i	Ui,B	Ii,A
		0.021
		0.037
		0.058
		0.082
		0.097

Известно, что функция линейная.

Так как при U = 0 (крайнее нижнее по схеме на рис.1.1 положение движка резистора R1) I = 0, то график уравнения линейной регрессии проходит через нуль координатной системы, а это уравнение имеет вид:

Для уравнения линейной регрессии 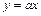функция имеет вид:

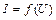, (1.7)

где - .

Уравнение для определения коэффициента а, с учетом формул (1.2) и (1.7), теперь будет иметь вид:

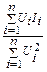= (1.8)

Соответственно, среднеквадратическое отклонение для уравнения линейной регрессии, с учетом формул (1.3) и (1.7) имеет вид:

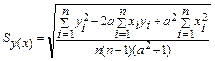== (1.9)

Так как n = 5, вычисляем выражения под знаком суммы для формул (1.8) и (1.9):

(1.10)

(1.11)

(1.12)

Коэффициент а линейной регрессии определим по формуле (1.8) подстановкой результатов вычислений (1.10) и (1.12):

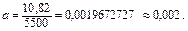
Искомая функция имеет вид:

(1.13)

Среднеквадратичное отклонение определяем путем подстановки в формулу (1.9) результатов вычислений (1.10), (1.11) и (1.12):

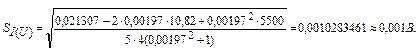
2. Чтобы построить график уравнения линейной регрессии, найдем I для U = 60 B по формуле (1.10):

.

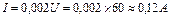Известно, что функция линейна и проходит через нуль координатной системы. Для построения графика соединяем прямой линией точку 0 начала координат и точку (U = 60 В; I = 0.12 А). График уравнения линейной регрессии изображен на рис. 1.2.

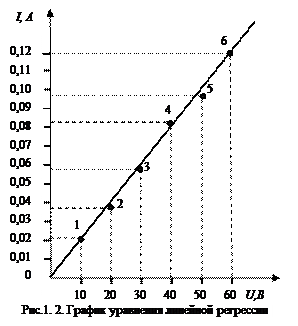
Точки 1,2,3,4,5 построены по экспериментальным данным пунктов 1-5 соответственно табл.1, а точка 6 по расчетным данным, полученным по формуле (1.13).

3. Используя формулу (1.6) определим неизвестное сопротивление R_Х:

R_Х = 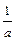= 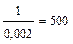Ом.

4. Вывод: малое значение S_y(x) свидетельствует о близости эмпирических данных и регрессионной прямой.

Пример решения аналогичной задачи рассматривается в [8], стр. 290 – 294.

Варианты заданий:

Номер варианта выбирать согласно номеру в журнале группы.

Номер варианта	i	Ui,B	Ii,A	Номер варианта	i	Ui,B	Ii,A
			0,041 0,081 0,120 0,159 0,203				0,035 0,072 0,107 0,144 0,178
			0,038 0,073 0,112 0,147 0,184				0,038 0,077 0,115 0,153 0,192
			0,035 0,070 0,104 0,141 0,176				0,034 0,066 0,102 0,132 0,167
			0,039 0,079 0,117 0,158 0,195				0,035 0,068 0,104 0,137 0,172
			0,036 0,072 0,108 0,146 0,183				0,038 0,075 0,114 0,150 0,188
			0,033 0,065 0,098 0,132 0,164				0,030 0,060 0,089 0,119 0,150
			0,033 0,067 0,102 0,136 0,169				0,029 0,058 0,087 0,115 0,145
			0,032 0,064 0,095 0,126 0,159				0,028 0,057 0,085 0,113 0,142
			0,031 0,063 0,094 0,125 0,156				0,027 0,055 0,082 0,110 0,138
			0,032 0,064 0,097 0,129 0,160				0,026 0,053 0,082 0,107 0,134
			0,031 0,062 0,092 0,123 0,153				0,028 0,056 0,084 0,112 0,140
			0,029 0,059 0,088 0,117 0,148				0,027 0,054 0,082 0,109 0,136
			0,028 0,057 0,085 0,115 0,143				0,026 0,053 0,079 0,104 0,132
			0,030 0,061 0,091 0,122 0,152	...	...	...	...

Дата добавления: 2014-11-16