Коэф-т корреляции как хар-ка статистич.связи. Некоррелир-сть и независимость сл.вел

Если X и Y независимы, то

Свойства:

1.

2. если 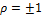, то между X и Y имеется лин.зависимость Х=a+b*Y

3. Показыв.степень лин.завис-ти, когда Чем ближе к 1, тем коэфф.корреляции. (мера (индикатор) лин.зав-сти между X и Y)

Законы больших чисел и предельные теоремы. Теорема Бернулли. Теорема Чебышева.

При очень большом числе сл.явлений средний их рез-т практически перестает быть случайным и может предсказан с большой степенью определенности.

1) Сходимость по вер-сти

Х₁,Х₂,…Х_n

Посл-сть сходится по вер-сти к сл.в.А при

при большом числе опытов частота соб.приближается в вер-сти этого соб.

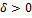Если сущ. то и , что

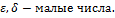
2) Неравенство Чебышева

Пусть Х – любая сл.вел.

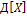
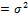
t 0 – люб.число

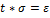
=1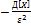

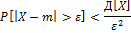
Каково бы ни было положит.число , вер-сть того, что вел.Х отклонится от своего мат.ожидания не меньше, чем на 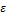огранич.сверху.

Предельные теоремы дают возможность не только осущ-ть научн.прогнозы, в обл-сти сл.явл-ний, но и оценивать точность этих прогнозов.

(Закон больших чисел)

Предельные теоремы дают возможность не только осущ-ть научн.прогнозы, в обл-сти сл.явл-ний, но и оценивать точность этих прогнозов.

(Закон больших чисел)

Теорема Чебышева.

Пуст ь Х₁, Х₂, …Х_n – незав.сл.вел. имеют одно и тоже расрп-е.

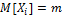
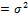
Тогда

При достаточно большом числе независ.опытов со.ариф-ое наблюденных значений сл.вел.сходятся по вер-сти к ее мат.ожид-ю.

Док-ство: воспольз.нер-вом Чебышева.

Сл.в.Х

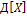
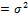
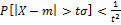, t=const

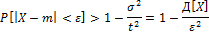
Сколь угодна сход.по вер-сти близка к 1

Теорема Бернулли. (следствие т.Чебышева)

(устанавл.связь между астотой соб.и его вер-стью).

Пусть проводится (n) экспериментов. В каждом эксперименте появл.соб.А (успех) с вер-стью (р).

И появл.(Ā) (неуспех) с вер-тью q=1-p

Рез-ты экспер-тов не влияют друг на друга.

При неогранич.увеличении числа опытов h частота соб.А сходится по вер-сти к его вер-сти р.

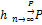
k – число успехов в n испытаний; n –число экспер-тов.

Центральная предельная теорема. Теорема Муавра-Лапласа.

(колич-ная форма закона больших чисел)

Все формы ЦПТ посвящены установлению условий, при кот.возникает норм.закон распр.

N(m,

В теории стрельбы N(m, играет особо важную роль, т.к в боль-ве случаев практики корд-ты точек попадания и точек разрыва снарядов распределяются по норм. Закону.

Х₁, Х₂, …Х_n – незав.сл.вел.с одним и тем же распр-ем

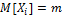
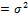
X= Х₁+ …+Х_n – сумма случ.вел.

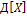
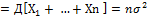
Рассм.нормир-ную случ.вел. (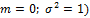

Ф-ция растр-я равномерно по х.

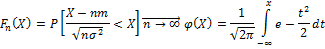
Ф-ция распр-я норм.зак.с пар-ми N(0;1)

Следствие (ЦПТ)

1) Х=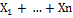

)

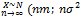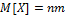
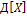
2)

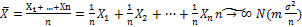
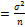
3)

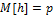
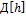
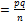
4) Теорема Муавра-Лапласа.

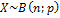
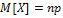
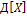
Х=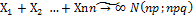

Напр.число успехов лежит в интервале (a,b)

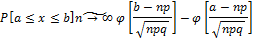
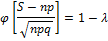
Распределение сред.ариф-го независ. с.в. и отн-ной частоты при большом числе наблюдений n.

Среднее ариф.сл.вел.

Х₁, Х₂, …Х_n – незав.сл.вел., имеющ.одно и тоже распр-е

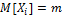
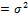
Среднее арифм.(выборочное среднее)

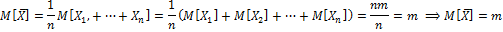
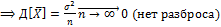
Относит.частота и свойства.

n – объем выборки

к – число эл-тов выборки, кот.облад.св-вом А относит.частота появления св-ва А

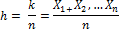
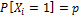
	q	p

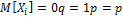
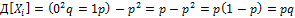
Статистика.

17

Предмет мат.статистики. Осн.понятия: выборка, генер.сов-сть статистики. Распр-е выборки, выборочные моменты. Выборочный вектор.

Мат.статистика позволяет получать обоснован.выводы о параметрах, видах распр-й и др.св-вах сл.вел.по конечной совокупности наблюдений над ними – выборке. (предмет: описание и анализ данных наблюдений).

Выборка – мн-во случаев, с помощью определен.процедуры выбран.из ген.сов-сти для участия в исследовании.

Ген.сов-сть – сов-сть всех объектов (единиц), отн-но которых ученый намерен делать выводы при изучении конкр.проблемы.

Мн-во всех обследуемых объектов.

Статистика – измеримая числовая ф-ция от выборки, не зависящих от неизвестных пар-ров распр-я.

-осн.хар-ки ген.сов-сти (среднее дисперсия, т.д.)

Выборка должна быть репрезентативной. (давать правильное представл-е о ген.сов-сти)

Простой случ.выбор – все эл-ты ген.сов-сти должны иметь равные шансы попасть в выборку.

Закон распр-я сл.вел.Х назыв. распределением ген.сов-сти, а случ.вектор (Х₁,Х₂,…Х_n) – выборочным вектором.

Часто требуется охарак-ть ген.сов-сть некоторыми колич.показателями, кот.определяют положение центра распр-я, рассеяние (разброс) и асимметрию, что дает возможность сравнить одну сов-сть данных с другой.

По выборке можно определить приближенные значения (оценки) этих числ.хар-к, кот.называются выборочными характеристиками.

Оценки моментов:

+

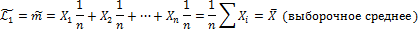
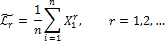
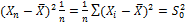
Распр-е выборки – распр-е дискр.сл.вел., приним.значения Х₁,Х₂,….Х_n с вероятностями 1∕n.

Задача стат.оценивания. Несмещенность и состоятельность оценок, эффективность оценок.

Задача – нахождение приближенных значений – оценок параметров распределения по выборке.

Статистика – некоторая ф-ция эл-тов выборки.

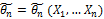
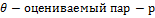
Вид распр-я известен

Критерии для выбора наилучшей оценки.

Дата добавления: 2014-11-16