
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Закон сохранения импульса и момента импульса
|
|
|
|
При взаимодействии частиц системы между собой полный вектор импульса системы остается постоянным в случаях, когда
а) 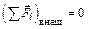 , б)
, б)  и время взаимодействия очень мало. В этих случаях
и время взаимодействия очень мало. В этих случаях  , где
, где 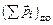 – векторная сумма импульсов частиц, которые существовали до взаимодействия,
– векторная сумма импульсов частиц, которые существовали до взаимодействия,  – векторная сумма импульсов всех частиц, которые будут существовать после взаимодействия. Если
– векторная сумма импульсов всех частиц, которые будут существовать после взаимодействия. Если 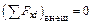 , то сохраняется только проекция полного импульса системы на ось x,
, то сохраняется только проекция полного импульса системы на ось x,  .
.
При взаимодействии частиц системы между собой полный вектор момента импульса системы остается постоянным в случаях, когда
а) 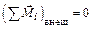 , б)
, б)  и время взаимодействия очень мало. В этих случаях
и время взаимодействия очень мало. В этих случаях 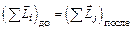 где
где 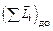 – векторная сумма моментов импульсов частиц, которые существовали до взаимодействия,
– векторная сумма моментов импульсов частиц, которые существовали до взаимодействия, 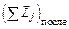 – векторная сумма моментов импульсов всех частиц, которые будут существовать после взаимодействия. Если
– векторная сумма моментов импульсов всех частиц, которые будут существовать после взаимодействия. Если  , то сохраняется только проекция момента импульса системы на ось z
, то сохраняется только проекция момента импульса системы на ось z 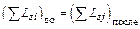 (часто относительно закрепленной оси вращения).
(часто относительно закрепленной оси вращения).
Момент импульса частицы  , где
, где 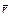 – радиус-вектор частицы,
– радиус-вектор частицы, 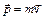 – импульс частицы.
– импульс частицы.  , где a – угол между
, где a – угол между 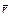 и
и  . Для твердого тела, вращающегося вокруг закрепленной оси z
. Для твердого тела, вращающегося вокруг закрепленной оси z 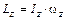 , где
, где 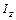 – момент инерции тела относительно оси z,
– момент инерции тела относительно оси z, 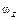 – угловая скорость.
– угловая скорость.
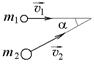 10-1. Маленький пластилиновый шарик массы m 1 движется горизонтально со скоростью
10-1. Маленький пластилиновый шарик массы m 1 движется горизонтально со скоростью 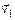 . Под углом a к направлению его движения летит второй шарик массы m 2 со скоростью
. Под углом a к направлению его движения летит второй шарик массы m 2 со скоростью 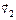 и сталкивается с первым. Шарики слипаются и движутся под углом b к первоначальному направлению движения второго шарика. Найдите
и сталкивается с первым. Шарики слипаются и движутся под углом b к первоначальному направлению движения второго шарика. Найдите 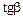 . Если
. Если  1 кг,
1 кг,  2 кг,
2 кг, 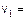 1 м/с,
1 м/с, 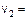 2 м/с, a = 30°.
2 м/с, a = 30°.
 10-2. Маленький пластилиновый шарик массы m 1 движется горизонтально со скоростью
10-2. Маленький пластилиновый шарик массы m 1 движется горизонтально со скоростью 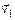 . Под углом a к направлению его движения летит второй шарик массы m 2 со скоростью
. Под углом a к направлению его движения летит второй шарик массы m 2 со скоростью 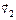 и сталкивается с первым. Шарики слипаются и движутся под со скоростью
и сталкивается с первым. Шарики слипаются и движутся под со скоростью 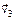 . Найдите после удара модуль импульса шариков. Если
. Найдите после удара модуль импульса шариков. Если  1 кг,
1 кг,  2 кг,
2 кг, 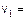 1 м/с,
1 м/с, 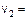 2 м/с, a = 45°.
2 м/с, a = 45°.
10-3. Маленький пластилиновый шарик массы m 1 движется горизонтально со скоростью 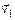 . Перпендикулярно к направлению его движения летит второй шарик массы m 2 со скоростью
. Перпендикулярно к направлению его движения летит второй шарик массы m 2 со скоростью 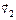 и сталкивается с первым. Шарики слипаются и далее движутся вместе. Найдите после удара а) модуль импульса шариков; б) модуль скорости шариков. Если
и сталкивается с первым. Шарики слипаются и далее движутся вместе. Найдите после удара а) модуль импульса шариков; б) модуль скорости шариков. Если  1 кг,
1 кг,  2 кг,
2 кг, 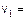 1 м/с,
1 м/с, 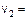 2 м/с.
2 м/с.
10-4. Маленький пластилиновый шарик массы m 1 движется горизонтально со скоростью 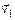 . Перпендикулярно к направлению его движения летит второй шарик массы m 2 со скоростью
. Перпендикулярно к направлению его движения летит второй шарик массы m 2 со скоростью 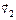 и сталкивается с первым. Шарики слипаются и далее движутся вместе под углом b к первоначальному направлению движения первого шарика шарика. Найдите
и сталкивается с первым. Шарики слипаются и далее движутся вместе под углом b к первоначальному направлению движения первого шарика шарика. Найдите 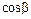 и
и 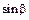 . Если
. Если  1 кг,
1 кг,  2 кг,
2 кг, 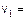 1 м/с,
1 м/с, 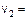 2 м/с.
2 м/с.
 10-5. На горизонтальной плоскости лежит тонкий однородный стержень массы m =1 кг и длины l, который может вращаться вокруг вертикальной оси, проходящей через центр масс стержня С. Под углом a =30° к стержню в той же плоскости движется маленький пластилиновый шарик такой же массы m со скоростью
10-5. На горизонтальной плоскости лежит тонкий однородный стержень массы m =1 кг и длины l, который может вращаться вокруг вертикальной оси, проходящей через центр масс стержня С. Под углом a =30° к стержню в той же плоскости движется маленький пластилиновый шарик такой же массы m со скоростью  = 1 м/с. Шарик прилипает к концу стержня, и система приобретает угловую скорость вращения w. Найти угловую скорость вращения системы после удара, если l = 1 м.
= 1 м/с. Шарик прилипает к концу стержня, и система приобретает угловую скорость вращения w. Найти угловую скорость вращения системы после удара, если l = 1 м.
 10-6. На горизонтальной плоскости лежит тонкий однородный стержень массы m =1 кг и длины l, который может вращаться вокруг вертикальной оси, проходящей через конец стержня О. Под углом a =30° к стержню в той же плоскости движется маленький пластилиновый шарик такой же массы m со скоростью
10-6. На горизонтальной плоскости лежит тонкий однородный стержень массы m =1 кг и длины l, который может вращаться вокруг вертикальной оси, проходящей через конец стержня О. Под углом a =30° к стержню в той же плоскости движется маленький пластилиновый шарик такой же массы m со скоростью  = 1 м/с. Шарик прилипает к концу стержня, и система приобретает угловую скорость вращения w. Найти угловую скорость вращения системы после удара, если l = 1 м.
= 1 м/с. Шарик прилипает к концу стержня, и система приобретает угловую скорость вращения w. Найти угловую скорость вращения системы после удара, если l = 1 м.
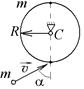 10-7. Тонкий однородный диск массы m = 1 кг и радиуса R может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его центр С. Под углом a =30° к вертикали в плоскости вращения диска движется маленький пластилиновый шарик такой же массы m со скоростью
10-7. Тонкий однородный диск массы m = 1 кг и радиуса R может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его центр С. Под углом a =30° к вертикали в плоскости вращения диска движется маленький пластилиновый шарик такой же массы m со скоростью  = 1 м/с. Шарик прилипает к нижней точке неподвижно висящего диска, и система приобретает угловую скорость вращения w.. Найти угловую скорость вращения системы после удара, если R = 1 м.
= 1 м/с. Шарик прилипает к нижней точке неподвижно висящего диска, и система приобретает угловую скорость вращения w.. Найти угловую скорость вращения системы после удара, если R = 1 м.
 10-8. Тонкий однородный стержень массы m = 1 кг и длины l может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конец. С разных сторон на стержень горизонтально в той же плоскости налетают два одинаковых пластилиновых шарика той же массы m с одинаковыми скоростями
10-8. Тонкий однородный стержень массы m = 1 кг и длины l может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конец. С разных сторон на стержень горизонтально в той же плоскости налетают два одинаковых пластилиновых шарика той же массы m с одинаковыми скоростями  = 1 м/с. Первый шарик застревает в центре стержня, второй – в нижнем конце, и система приобретает угловую скорость w. Найти угловую скорость вращения системы после удара, если l = 1 м.
= 1 м/с. Первый шарик застревает в центре стержня, второй – в нижнем конце, и система приобретает угловую скорость w. Найти угловую скорость вращения системы после удара, если l = 1 м.
 10-9. Тонкий однородный стержень массы m =1 кг и длины l может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конец O. Горизонтально в той же плоскости на стержень налетает пластилиновый шарик той же массы m со скоростью
10-9. Тонкий однородный стержень массы m =1 кг и длины l может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конец O. Горизонтально в той же плоскости на стержень налетает пластилиновый шарик той же массы m со скоростью  = 1 м/с. Шарик застревает в точке А стержня на расстоянии х=
= 1 м/с. Шарик застревает в точке А стержня на расстоянии х=  от точки О, и система приобретает угловую скорость w. Найти угловую скорость вращения системы после удара, если l = 1 м.
от точки О, и система приобретает угловую скорость w. Найти угловую скорость вращения системы после удара, если l = 1 м.

 10-10. Два невесомых стержня длины b соединены под углом a1 = 60° и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью w = 2 рад/с. На конце одного из стержней прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно увеличился до a2 = 120°. С какой угловой скоростью стала вращаться такая система?
10-10. Два невесомых стержня длины b соединены под углом a1 = 60° и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью w = 2 рад/с. На конце одного из стержней прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно увеличился до a2 = 120°. С какой угловой скоростью стала вращаться такая система?
Литература
1. Савельев И.В. Курс общей физики: учебное пособие для вузов:[в 3 т.]. Т.1. Механика. Молекулярная физика / И.В. Савельев.- 5-е изд. стер. — СПб. и др.: Лань, 2006. - 432 с.
2. Савельев И.В. Сборник вопросов и задач по общей физике: учеб. пособие для втузов / И.В.Савельев.— СПб. и др.: Лань, 2005. - 288 с.
3. Стрелков С.П. Сборник задач по общему курсу физики: в 5 кн. - 5-е изд., стер.— М: Физматлит: Лань, 2006.— (Общий курс физики). Кн. 1: Механика / С. П. Стрелков [и др.]; под ред. И. А. Яковлева. - 2006. - 240 с.
4. Матвеев А.Н. Механика и теория относительности: Учебник для вузов / А.Н.Матвеев.- 3-е изд. - М.: ОНИКС 21 век: Мир и образование, 2003. - 432 с.
5. Трофимова Т.И. Сборник задач по курсу физики с решениями: учеб. пособие для вузов / Т.И.Трофимова.- 8-е изд. перераб. - М.: Высш. шк., 2007. - 591 с.
6. Трофимова Т.И. Основы физики: учеб. пособие:в 5 кн. Кн.1. Механика / Т.И.Трофимова.- М.: Высш. шк., 2007.- 220с
7. Трофимова Т.И. Справочник по физике для студентов и абитуриентов / Т.И.Трофимова.— М.: Астрель:АСТ: Профиздат, 2005. - 399 с.
8. Яворский Б.М. Справочник по физике для инженеров и студентов вузов / Б. М. Яворский, А. А. Детлаф, А. К. Лебедев.- 8-е изд., перераб. и испр. - М.: ОНИКС: Мир и Образование, 2007. - 1055 с.
9. Полянин А.Д. Универсальный справочник. Высшая математика. Физика. Теоретическая механика. Сопротивление материалов / А.Д.Полянин [и др.].- М.: АСТ:Астрель: Профиздат, 2005. - 480 с.
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 1095; Нарушение авторских прав?; Мы поможем в написании вашей работы!