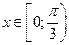КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Краткие теоретические сведения. 1. Определение обратной функции:
1. Определение обратной функции:
Если функция 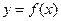 задает биективное отображение
задает биективное отображение 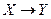 , то функция
, то функция  ,
,  называется обратной функцией к функции
называется обратной функцией к функции 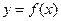 .
.
Функции 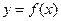 ,
, 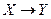 и
и  ,
,  называются взаимно обратными.
называются взаимно обратными.
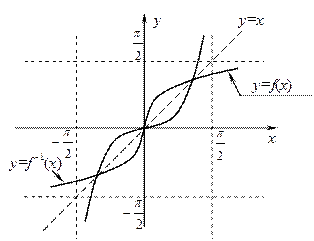
2. Графики взаимно обратных функций:
Если у обратной функции переобозначить аргумент на x, а функцию на y, то графики двух взаимно обратных функций
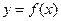 ,
,  и
и 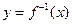 ,
, 
на плоскости xOy будут иметь осевую симметрию относительно биссектрисы первого и третьего координатного угла (относительно прямой y=x).
Аудиторные задания
Задача 1
Для данной функции 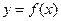 найдите обратную функцию
найдите обратную функцию 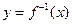 ,постройте графики обеих функций в одной системе координат, запишите ООФ и ОЗФ каждой из взаимно обратных функций:
,постройте графики обеих функций в одной системе координат, запишите ООФ и ОЗФ каждой из взаимно обратных функций:
1)  ; 2)
; 2) 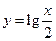 ; 3)
; 3) 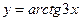 ; 4)
; 4) 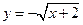 .
.
Ответы:
1)
если
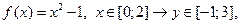 то
то
 ; ;
| 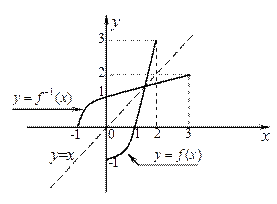
|
2)
если
 то
то
 ; ;
| 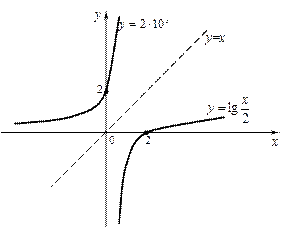
|
3)
если  то
то
 ; ;
| 
|
4)
если
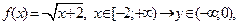 то
то
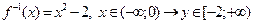 ; ;
| 
|
Задания для домашнего выполнения
Подготовиться к контрольной работе по «0» варианту.
Занятие 11. Контрольная работа №1
Цель занятия:
написать контрольную работу №1 (итоговый контроль по теме 1).
Контрольная работа №1 по теме "Введение в математический анализ",
вариант 0
Задача 1
Даны непрерывные множества  и
и  .
.
Требуется:
1) записать А и В промежутками и построить на одной координатной прямой;
2) охарактеризовать ограниченность А и В, указать их точные грани и экстремумы;
3) записать промежутками множества 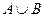 ,
, 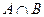 ,
, 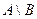 ,
, 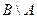 .
.
Задача 2
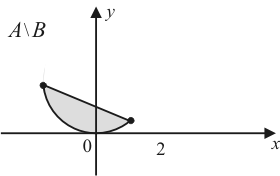
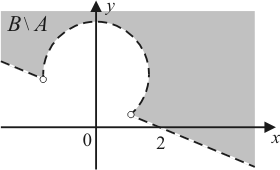
Построить множества точек на координатной плоскости xOy:
1) 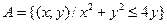 ,
, 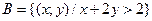 ;
;
2) 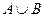 ,
, 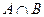 ,
, 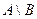 ,
, 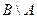
Задача 3
1) Найти ООФ и ОЗФ функции:  ;
;
2) Найти ООФ 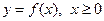 , если
, если 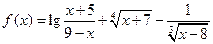 .
.
Задача 4
Дана функция 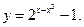 Требуется:
Требуется:
1) охарактеризовать четность  ;
;
2) найти множества  ,
, 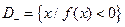 ,
,  .
.
Задача 5
Для данной функции  требуется:
требуется:
1) найти обратную функцию 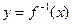 ;
;
2) построить графики обеих функций в одной системе координат;
3) записать ООФ и ОЗФ каждой из функций  и
и 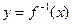 .
.
Задача 6
Дана функция 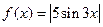 и множество
и множество 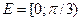 . Требуется:
. Требуется:
1) построить график функции 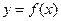 на ее естественной ООФ;
на ее естественной ООФ;
2) записать по графику основные характеристики функции:
ООФ, ОЗФ, нули функции, четность, периодичность, монотонность, локальные экстремумы, наибольшее и наименьшее значения функции на ООФ;
3) найти множество  ; изобразить отображение
; изобразить отображение  геометрически и указать, является ли оно биекцией.
геометрически и указать, является ли оно биекцией.
Ответы к задачам варианта 0 контрольной работы №1
Задача 1
|
 ,
,  ;
;
|
|

2) А – неограничено, т.к. является ограниченным сверху, но неограниченным снизу;
 ,
, 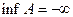 ;
;  ,
, 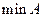 – не существует;
– не существует;
В –ограничено, т.к. является ограниченным и сверху и снизу;
 ,
, 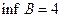 ;
;  – не существует,
– не существует, 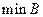 – не существует;
– не существует;
3) 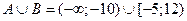 ;
; 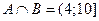 ;
;
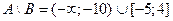 ;
; 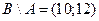 .
.
Задача 2
| 1) |  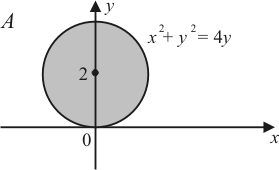
|    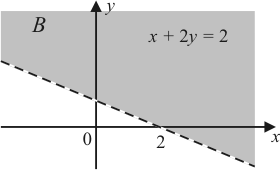
| ||||
| 2) | 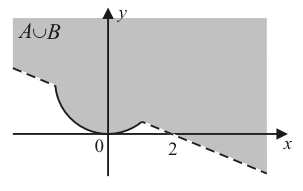
| 
| ||||
| 
|
Задача 3
1) ООФ  :
:  , ОЗФ
, ОЗФ  :
: 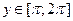 ;
;
2) ООФ 
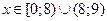 .
.
Задача 4
1) Данная функция свойством четности не обладает (т.е. не является ни четной, ни нечетной);
2)  ,
, 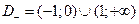 ,
, 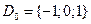 .
.
Задача 5
1) Если  , то
, то 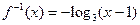 ;
;
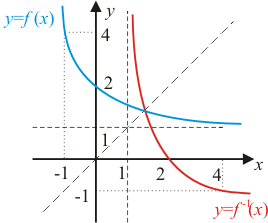
2) графики  и
и 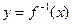 являются симметричными относительно прямой
являются симметричными относительно прямой  :
:


3) 
 ООФ:
ООФ:  , ОЗФ:
, ОЗФ:  ;
;
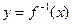
 ООФ:
ООФ:  , ОЗФ:
, ОЗФ: 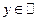 .
.
Задача 6
| 1) |  
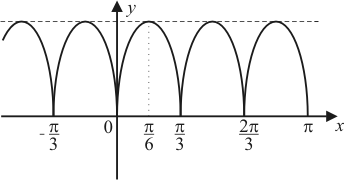
|
2) 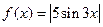
 ООФ:
ООФ:  , ОЗФ:
, ОЗФ:  ;
;
нули функции: 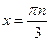 ,
,  ;
;
функция четная;
функция периодическая с наименьшим периодом 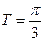 ;
;
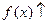 при
при  ,
,  ,
,
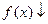 при
при  ,
,  ;
;
локальные экстремумы:
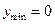 при
при 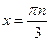 ,
,  ,
, 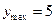 при
при 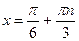 ,
,  ;
;
 ,
, 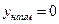 .
.
3) Если 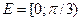 , то
, то  ;
;
отображение 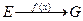 не является биекцией.
не является биекцией.
|




|




|



|
|
Дата добавления: 2014-11-16; Просмотров: 483; Нарушение авторских прав?; Мы поможем в написании вашей работы!
 ,
,