Центр ваги

Центр паралельних сил

ЦЕНТР ВАГИ

Зміст

9.1. Центр паралельних сил.

9.2. Центр тяжіння.

9.3. Центри тяжіння деяких плоских однорідних фігур.

9.4. Контрольні запитання.

9.5. Приклади розв’язування задач.

Якщо на тіло діє система паралельних сил P₁, P₂,..., P_n, то точка С, через яку проходить рівнодіюча R цієї системи сил, називається центром паралельних сил (рис.9.1).

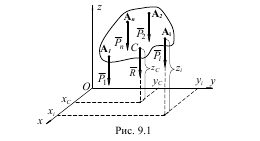
Координати центра паралельних сил визначаються за залежностями:

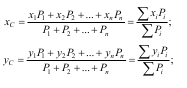
де x_i, y_i, z_i - координати точок прикладення сил P.

Центр паралельних сил має ту особливість, що через нього обов’язково буде проходити лінія дії рівнодіючої при повертанні ліній дії усіх сил системи навколо точок їх прикладення на один і той же кут в один і той же бік. Модулі сил при повертанні не повинні змінюватися.

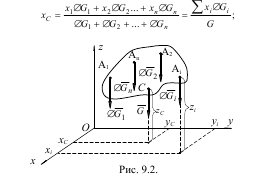Якщо тверде тіло знаходиться біля поверхні Землі, то на кожну матеріальну частину цього тіла діє сила тяжіння ∆G_i, яка напрямлена до центра Землі. Оскільки розміри тіла невеликі в порівнянні з розмірами Землі, то утворену систему сил можна розглядати як паралельну. Рівнодіюча цієї паралельної системи сил G, яка дорівнює їх сумі, називається вагою тіла, а центр цієї системи - точка С називається центром ваги тіла (рис.9.2). Координати центра тяжіння твердого тіла можна визначити як координати центра паралельних сил:

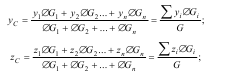
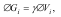Якщо тіло однорідне, тобто питома вага не Тоді формули для визначення координат центра тяжіння

твердого тіла набудуть вигляду: змінюється за об’ємом (γ =const), то:; G =Vγ,де:

Тоді формули для визначення координат центра тяжіння твердого тіла набудуть вигляду:

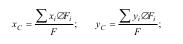Положення центра тяжіння однорідного тіла залежить тільки від форми об’єму, що займає тіло, і називається центром тяжіння цього об’єму. Якщо однорідне тіло має форму тонкої пластини, то його можна розглядати як матеріальну плоску фігуру. В цьому випадку положення центра тяжіння плоскої фігури визначається двома координатами C_х та C_у і залежить від форми площі фігури:

Центр тяжіння однорідної пластини називається центром ваги плоскої фігури. Якщо виділений елементарний об’єм ∆V_i (площу елементарної площадки у плоскому випадку) спрямувати до нуля, то формули для обчислення координат центра тяжіння набудуть інтегрального вигляду:

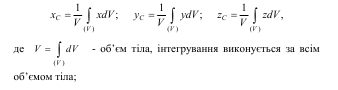а) для однорідного твердого тіла:

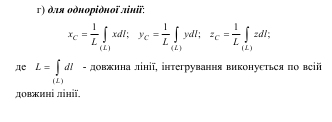
9.3. Центри ваги деяких плоских однорідних фігур

Для спрощення визначення центра тяжіння використовуються наступні допоміжні правилами:

1. Якщо тіло має площину симетрії, то центр тяжіння лежить на цій площині.

2. Якщо тіло симетричне відносно осі, то центр тяжіння лежить на цій осі.

3. Якщо тіло симетричне відносно точки, то центр тяжіння лежить в центрі симетрії.

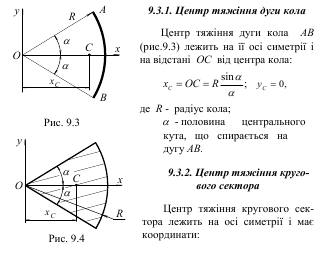4. Якщо тіло складається з декількох частин, центри тяжіння яких можна визначити, то центр тяжіння такого тіла знаходять як центр тяжіння декількох матеріальних точок, а саме тих, в яких розташовані ваги кожної окремої частини тіла.

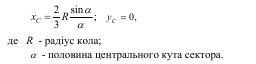
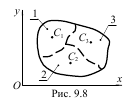Найбільш поширений спосіб визначення положення центра тяжіння однорідного тіла складної форми полягає в тому, що його розбивають на такі частини, положення центрів тяжіння яких відомо, або може бути легко визначене.

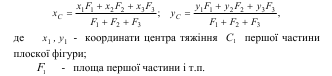Наприклад, однорідну плоску фігуру (рис.9.8) розбивають на три частини 1,2 і 3, положення центрів тяжіння яких, C₁, C₂, C₃, можна визначити. Координати центра тяжіння фігури С визначається за формулами:

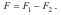Цим способом зручно користуватися і при визначенні положення центра тяжіння плоскої фігури, з якої вирізана деяка частина (рис.9.9). В цьому випадку, площу плоскої фігури можна записати у вигляді різниці площ суцільної фігури 1 (площа додатна) і вирізаної частини 2 (площа від’ємна), тобто

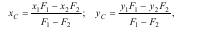Координати центра тяжіння фігури дорівнюють: Координати центра тяжіння фігури дорівнюють:

де x₁,у₁- координати центра тяжіння суцільної фігури 1, площа якої дорівнює F₁; х₂, у₂ - координати центра тяжіння вирізаної частини 2, площа якої дорівнює - F₂.

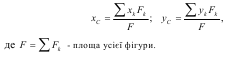Перший з цих методів має назву “метод розбиття”, другий – “метод доповнення”, або “метод від’ємних мас”. В загальному випадку формули для визначення центру тяжіння плоскої фігури мають вигляд:

9.4. Контрольні запитання

1. Яку властивість має центр паралельних сил?

2. За якими формулами обчислюються координати центра паралельних сил?

3. Як визначається положення центра тяжіння площі, якщо відомі положення центрів тяжіння окремих її частин?

4. Якими допоміжними теоремами користуються при визначенні положення центра тяжіння?

9.5. Приклади розв’язування задач

Задача № 1

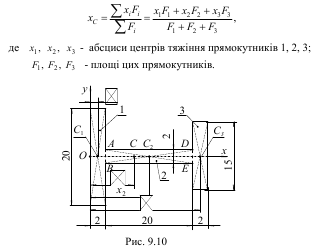
Знайти центр ваги двотаврового профілю, розміри якого в сантиметрах вказані на рис.9.10.

Розв’язок. Оскільки форма перерізу має вісь симетрії, то вісь Ох напрямимо вздовж осі симетрії, а вісь Оу перпендикулярно до неї. В силу симетричності профілю відносно осі Ох центр тяжіння буде лежати на цій осі, тобто

у _С= 0. Лініями АВ і DE поділимо профіль на три прямокутника 1, 2 і 3. Запишемо рівняння для визначення абсциси центра тяжіння площі:

Задача №2

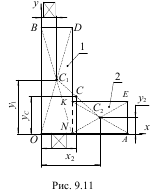
Знайти координати центра тяжіння поперечного перетину різнобокого кутника (рис.9.11), полки якого мають ширину ОА=а, ОВ=b і товщину АЕ=ВD=d.

Розв’язок. Розділимо перетин лінією КN на два прямокутника

ОВDN і NKEA, центри тяжіння яких лежать на перетині відповідних

діагоналей. Запишемо формули для координат х_С і у_С центра

тяжіння перетину:

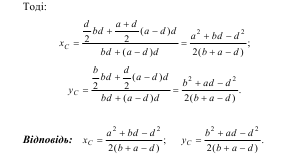
Задача № 3

Визначити положення центра ваги плоскої фігури (рис.9.12), обмеженої півколом АОВ радіуса R і двома прямими

рівної довжини АD і ВD, причому ОD = 3R.

Розв’язок. Дана площа має вісь симетрії, вздовж якої направимо вісь Ох₁. Оскільки центр тяжіння площі С лежить на осі симетрії, то у_С = 0. Розділимо площу АОВD лінією АВ на дві частини: півколо АОВ і рівнобедрений трикутник АDВ. Абсциса центра ваги площі х_С буде дорівнювати:

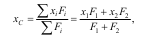
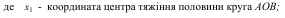
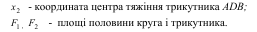
Центр тяжіння трикутника лежить на перетині його медіан (розділ 9.3.4). Оскільки трикутник АDВ рівнобедрений, то лінія О₁D буде його медіаною і відстань О₁С₂ буде дорівнювати третій частині від О₁D:

КІНЕМАТИКА

Кінематикою називається розділ теоретичної механіки, в якому вивчається механічний рух тіл з геометричної точки зору, тобто без урахування їх мас і сил, що на них діють.

Рух тіл в кінематиці розглядають по відношенню до деякої системи координат, що пов’язана з іншим тілом, наприклад, із Землею.

Основна задача кінематики полягає в тому, що за рівняннями, які визначають закон руху даного тіла, треба знайти всі кінематичні характеристики руху тіла (траєкторії різних точок, їх швидкості та прискорення).

Кінематика ділиться на кінематику точки і кінематику твердого тіла.

В першому розділі навчального посібника розглядаються наступні теми кінематики:

• Кінематика точки.

• Поступальний рух тіла.

• Обертальний рух тіла навколо нерухомої осі.

• Плоский рух тіла.

• Складний рух точки.

КІНЕМАТИКА ТОЧКИ

Координатний спосіб означення руху

Зміст

1.1. Траєкторія і рівняння руху точки.

1.2. Визначення швидкості і прискорення точки при координатному способі означення її руху.

1.3. Порядок розв’язування задач з кінематики точки.

1.4. Контрольні запитання.

1.5. Приклади розв’язування задач.

1.1. Траєкторія і рівняння руху точки

Означити рух точки – це значить вказати правило, за яким в будь який момент часу t можна визначити положення точки в просторі.

Розрізняють три способи означення руху точки: координатний; векторний; природний.

Координатний спосіб означення руху точки

Положення точки M у просторі при координатному способі означення руху визначається трьома координатами: х, у, z (рис.1.1). Якщо точка рухається, то ці координати з часом безперервно змінюються. Таким чином, для означення руху точки достатньо задати функціональні залежності виду:

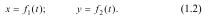Рівняння (1.1) називаються рівняннями руху точки в прямокутних координатах.

Рух точки в площині, наприклад Oxy, визначається двома рівняннями руху:

Для означення прямолінійного руху точки, наприклад, по осі Ox, достатньо одного рівняння:

Визначення траєкторії точки при координатному способі означення її руху.

Траєкторією називається та сукупність точок, через які послідовно проходить тіло під час руху в даній системі відліку.

Траєкторія – одна із основних характеристик, яка дає уявлення про рух в цілому. Першою ознакою, за якою виконується розподіл рухів на різні види, є траєкторія.

Визначення траєкторії є однією із важливих частин задач механіки.

В залежності від форми траєкторії рух відносять до прямолінійного, або криволінійного руху.

Рівняння руху точки (1.1) ч (1.3) можна розглядати як рівняння траєкторії в параметричній формі.

Для того, щоб отримати рівняння траєкторії в звичайній формі, треба з рівнянь руху виключити час t. Так, виключивши t з рівнянь руху (1.2), дістанемо одне рівняння виду:

яке являє собою рівняння лінії на площині Oxy.

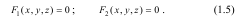Якщо виключити час t з рівнянь руху (1.1), то дістанемо рівняння виду:

Кожне з рівнянь системи (1.5) є рівнянням деякої поверхні, а разом – рівнянням траєкторії, яка являє собою лінію перетину цих поверхонь.

1.2. Визначення швидкості і прискорення точки при координатному способі означення її руху

Швидкість точки – векторна величина, яка характеризує зміну положення точки в просторі з часом.

Прискорення точки – векторна величина, яка характеризує зміну вектора швидкості з часом.

У випадку координатного способу означення руху точки за відомими залежностями для координат точки (1.1) спочатку визначають проекції вектора швидкості на координатні осі:

а потім модуль швидкості точки:

Напрямок вектора швидкості V визначається через напрямні косинуси кутів, які цей вектор утворює з відповідними осями координат:

Проекції вектора прискорення на координатні осі відповідно дорівнюють:

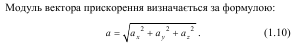
Напрямок вектора прискорення a також визначається через напрямні косинуси кутів, які цей вектор утворює з відповідними осями координат:

1.3. Порядок розв’язування задач з кінематики точки

Розв’язування задач на визначення закону руху точки та рівняння її траєкторії виконується в такій послідовності:

1. Обирається нерухома система координат, початок якої визначають, виходячи з умов задачі.

2. За умовами задачі в обраній системі координат складають рівняння руху точки, тобто знаходять залежність координат точки від часу.

3. Із складених рівнянь руху точки можна визначити її положення в будь-який момент часу, встановити напрям її руху, знайти траєкторію і т.д.

Якщо за умовою задачі треба визначити швидкість і прискорення точки, то краще дотримуватись такої послідовності: 1. Обрати систему координат.

2. В обраній системі координат скласти рівняння руху (іноді вони задані в умовах задачі).

3. За рівняннями руху точки визначити проекції швидкості на осі системи координат, величину швидкості та її напрям.

4. Визначити проекції прискорення точки на осі системи координат, величину прискорення та його напрям.

1.4. Контрольні запитання

1. Що називається траєкторією?

2. Як за рівняннями руху точки в координатній формі визначити її траєкторію?

3. Що називається швидкістю та прискоренням точки?

4. Як визначити проекції векторів швидкості та прискорення точки на нерухомі осі прямокутної системи координат?

5. Як визначити напрями векторів швидкості та прискорення при координатному способі означення руху?

1.5. Приклади розв’язування задач

Задача № 1

Рух точки на площині визначається рівняннями:

Визначити рівняння траєкторії і напрям руху точки. Розв’язок. Рівняння траєкторії задано в параметричній формі, координати х і у залежать від параметра t (часу).

Щоб отримати рівняння траєкторії в координатній формі, тобто у вигляді залежності у = f(х), необхідно виключити з обох рівнянь руху час t.

Піднесемо до квадрату ліві та праві частини рівнянь руху:

або

Доламо ці рівняння

Рівнянням траєкторії точки є еліпс з центром в початку системи координат, велика піввісь якого дорівнює 5-ти одиницям довжини (по осі Ох), а мала (по осі Оу) – 3-ом одиницям довжини (рис.1.2).

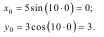
В початковий момент часу t =0 точка знаходиться в положенні M₀ з координатами:

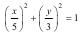В початковий момент руху (при зростанні t) координата х почне збільшуватися, а координата у − зменшуватися. Таким чином, точка буде рухатися за ходом годинникової стрілки.

Відповідь: а) рівняння траєкторії; б) точка рухається за ходом годинникової стрілки.

Задача №2

В механізмі (рис.1.3) тіло ОА (кривошип) обертається навколо нерухомого шарніра О, а тіло В (повзун) рухається зворотно-поступально по осі Ox. Точка А тіла АВ (шатуна) рухається за траєкторією точки А кривошипа, а точка В – за траєкторією повзуна. Визначити рівняння руху і траєкторію середньої точки М шатуна та рівняння руху повзуна В,, якщо в початковий момент повзун знаходився в крайньому правому положенні; кривошип ОA обертається зі сталою кутовою швидкістю

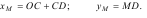Розв’язок. Для визначення траєкторії точки М зобразимо механізм у довільному положенні та складемо рівняння її руху в координатній формі. З рис. 1.3 видно, що:

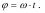Оскільки трикутник ОАВ рівнобедрений (ОА=АВ), то кути АВС і АОС рівні між собою і дорівнюють.

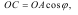З трикутника ОАС знайдемо відстань OC:

а з трикутника MBD відстані CD і MD:

Тоді:

Якщо підставити числові дані, то рівняння руху точки М набудуть вигляду:

Для знаходження траєкторії точки М піднесемо рівняння руху до квадрату і додамо:

Таким чином, траєкторією точки буде еліпс, одна піввісь якого, по осі Ох, складає 1,2 м, а друга, по осі

Оу, – 0,4 м. Визначимо координати точки В:

Таким чином, рівняння руху повзуна В буде мати вигляд:

КІНЕМАТИКА ТОЧКИ

Природний спосіб означення руху точки

Зміст

1.6. Природний спосіб означення руху точки.

1.7. Визначення швидкості і прискорення точки при природному способі означення її руху.

1.8. Контрольні запитання.

1.9. Приклади розв’язування задач.

1.6. Природний спосіб означення руху точки

Природний спосіб означення руху точки полягає в наступному.

1. Будь яким способом (рівнянням, графічно, вказівкою) задається траєкторія точки М₀ В(рис.1.5).

2. На траєкторії обирається деяка точка M₀ як початок відліку дуги і додатний напрям уздовж траєкторії (на рис. 1.5 зліва направо).

3. Положення точки М на траєкторії однозначно визначається довжиною дуги, яку беруть з відповідним знаком. При русі точки по траєкторії кожному моменту часу t відповідає певне значення S.

Таким чином, для визначення положення точки на траєкторії досить задати залежність:

яка називається природним рівнянням руху.

Природним способом означення руху точки зручно користуватися в тому випадку, коли відома траєкторія точки.

1.7. Визначення швидкості і прискорення точки приприродномуспособіозначенняїїруху

У випадку природного способу означення руху точки за відомим рівнянням руху (1.12) модуль вектора швидкості визначають за формулою:

Направлений вектор швидкості за дотичною до траєкторії точки в бік відліку координати S (рис.1.6), якщо

і в протилежний бік, якщо 0

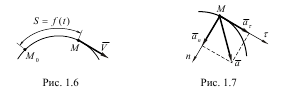
При визначенні прискорення з точкою М пов’язують рухому систему координат M _{n τ} (рис.1.7): тангенціальну вісь M_τ направляють за дотичною до траєкторії в бік швидкості точки; нормальну вісь M_n - за внутрішньою нормаллю до траєкторії (тобто, в бік центра її кривизни). Прискорення a розкладають на складові a_τ і а_n за осями обраної стеми координат, які відповідно називають дотичною (тангенціальною) і нормальною (доцентровою) складовими прискорення.

За модулем ці прискорення, відповідно, дорівнюють:

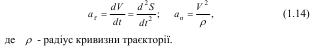
Нормальне прискорення завжди направлене до центра кривизни (за напрямом осі M_n), а дотичне прискорення – за віссю M_τ, якщо a_τ>0 і в протилежний бік, якщо a_τ<0.

Нормальне прискорення характеризує зміну напряму швидкост з плином часу. Якщо траєкторією точки є пряма лінія, тобто ρ = ∞, то 0a_n =0 і вектор швидкості не буде змінювати свого напряму.

Дотичне прискорення характеризує зміну швидкості за величиною з плином часу. Якщо точка рухається рівномірно

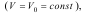то

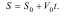a_τ=0, а шлях, що пройдено точкою, визначають за формулою:

У випадку рівномірно прискореного руху точки швидкість точки і шлях, який пройдено нею, визна-

чають за формулами:

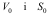В наведених формулах

- відповідно, початкові значення швидкості і пройденого шляху, а самі формули можна отримати шляхом інтегрування залежності для a_τ (1.14).

1.8. Контрольні запитання

1. В чому полягає природний спосіб означення руху точки?

2. Як визначити швидкість точки за модулем і за напрямом?

3. Що характеризують дотичне і нормальне прискорення точки?

4. Як визначити величину і напрям дотичного прискорення?

5. Як визначити величину і напрям нормального прискорення?

6. При якому русі точки дорівнює нулю дотичне прискорення і при якому – нормальне прискорення?

1.9. Приклади розв’язування задач

ПОСТУПАЛЬНИЙ ТА ОБЕРТАЛЬНИЙ ВИДИ РУХУ ТВЕРДОГО ТІЛА

Зміст

2.1. Поступальний рух твердого тіла.

2.2. Обертальний рух твердого тіла.

2.3. Рівномірний та рівнозмінний обертальний рух тіла.

2.4. Швидкість та прискорення точок тіла, що обертається.

2.5. Контрольні запитання.

2.6. Приклади розв’язування задач.

2.1. Поступальний рух твердого тіла

Поступальним називається такий рух твердого тіла, при якому довільна пряма, що незмінно пов’язана з тілом, увесь час залишається паралельною своєму початковому положенню. Для твердого тіла (рис.2.1) пряма АВ, що з’єднує дві довільні його точки, під час поступального руху не змінюється ні за довжиною, ні за напрямом. Це означає, що при поступальному русі точки А та В тіла мають однакові траєкторії (при накладанні збігаються) і в кожний момент часу однаковими будуть їх швидкості і прискорення, тобто:

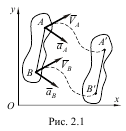
Таким чином, поступальний рух твердого тіла повністю визначається рухом будь-якої точки цього тіла, тобто задача визначення кінематичних характеристик поступального руху твердого тіла зводиться до задачі кінематики точки.

2.2. Обертальний рух твердого тіла

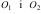Обертальним рухом називається такий рух твердого тіла, при якому будь-які дві точки тіла залишаються нерухомими. Якщо закріпити дві точки тіла (рис.2.2), то будуть нерухомими всі точки прямої O₁ O₂, яка називається віссю обертання. Траєкторіями усіх інших точок тіла, наприклад М, будуть кола з центрами на осі обертання.

Проведемо через вісь обертання zz (рис.2.3) дві площини: одну нерухому - А, а другу, площину В, жорстко пов’яжемо з тілом, що обертається. Двогранний кут ϕ між цими двома площинами однозначно визначає положення тіла, що обертається. Для визначення знака кута ϕ на осі обертання zz обирають додатний напрям (на рис.2.3 – вгору). Кут уважається додатним, якщо з додатного напряму осі обертання кут відносно нерухомої площини відкладений проти ходу годинникової стрілки і від’ємний, якщо за ходом.

Коли тіло обертається, кут ϕ безперервно змінюється з часом. Таким чином, для повної характеристики обертального руху треба задати рівняння виду: (2.1)

Рівняння (2.1) називається рівнянням обертального руху тіла.

Зміну кута повороту тіла з плином часу характеризує кутова швидкість ω.

Миттєва кутова швидкість ω є першою похідною від кута повороту за часом:

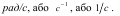Одиницею вимірювання кутової швидкості є радіан поділений на секунду і позначається як.

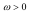Направлена кутова швидкість в бік миттєвого обертання тіла та, якщо збігається з напрямом відліку кута ω <0, якщо протилежна напряму відліку.

В техніці кут повороту пропорційний кількості обертів N,

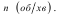
що зробило тіло за деякий проміжок часу. В цьому випадку кут повороту тіла в радіанах можна знайти за залежністю:

Кутову швидкість обертання тіла часто задають числом обертів за одну хвилину

Кутову швидкість ω в цьому випадку визначають за формулою:

де n - підставляють в об хв.

Зміну кутової швидкості з плином часу характеризує кутове прискорення ε.

Миттєве кутове прискорення ε визначається як перша похідна від кутової швидкості за часом, або друга похідна від кута повороту тіла:

Одиницею вимірювання кутового прискорення є радіан, поділений на секунду в квадраті, і позначається рад/с²,

або або

Направлене кутове прискорення за напрямом кутової швидкості, якщо знаки ω та ε збігаються, і проти напряму кутової швидкості, якщо знаки ω та ε різні.

2.3. Рівномірний та рівнозмінний обертальний рух тіла

У випадку рівномірного обертального руху тіла його кутова швидкість буде сталою (ω =const), а кутове прискорення дорівнює нулю (ω =0)

Кут повороту тіла в цьому випадку обчислюється за формулою:

де - початковий кут повороту тіла при t =0.

У випадку рівномірно змінного обертального руху тіла його кутове прискорення буде сталим (ε = const).

Кутова швидкість і кут повороту тіла в цьому випадку обчислюються за формулами:

де - відповідно кут повороту тіла і кутова швидкість в момент часу t =0.

2.4. Швидкість та прискорення точок тіла, що обертається

Якщо для тіла, що обертається, відомі кутова швидкість ωі кутове прискорення ε, то можна знайти швидкість V і прискорення a будь якої його точки.

Швидкість точки тіла, що обертається, дорівнює добутку кутової швидкості тіла на відстань від точки до осі обертання:

Вектор швидкості точки V направлений під прямим кутом до радіуса обертання ОМ (рис.2.4) в бік обертання тіла (в бік кутової швидкості ω).

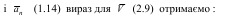Оскільки точка тіла, що обертається, рухається по криволінійній траєкторії (колу з радіусом кривизни R), то прискорення точки a можна розкласти на дві складові: тангенціальну (дотичну) a_τ і нормальну (доцентрову)a_n (рис.2.4). Підставивши в формули для a_τ

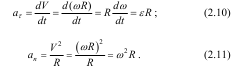
Нормальне прискорення a_n направлене від точки вздовж радіуса до центра обертання. Дотичне прискорення a

а_τ спрямоване перпендикулярно до радіуса в бік кутового прискорення ε.

Повне ж прискорення точки відповідно дорівнює:

2.5. Контрольні запитання

1. Який рух твердого тіла називається поступальним?

2. Який рух твердого тіла називається обертальним навколо нерухомої осі?

3. За якими формулами визначаються модулі кутової швидкості і кутового прискорення?

4. Як спрямований вектор швидкості тіла, що обертається?

5. Як визначити величину та напрям дотичного і нормального прискорення точки тіла, що обертається?

2.6. Приклади розв’язування задач

Задача №1

Вал починає обертатися зі сталим прискоренням із стану спокою. За перші 5 секунд вал робить 12,5 оберти. Визначити кутову швидкість вала в кінці проміжку часу, що розглядається.

Розв’язок. При рівноприскореному обертанні тіла кутова швидкість ω змінюється за законом:

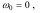
Оскільки за умовою задачі, то

Таким чином, для визначення кутової швидкості вала треба знайти його кутове прискорення ε. Кут повороту тіла при рівноприскореному обертанні визначається за формулою:

Кут повороту вала за число обертів N дорівнює:

Підставивши вираз для ε в формулу для ω отримаємо:

Задача № 2

Шків пасової передачі починає обертатися із стану спокою з сталим кутовим прискоренням і через 10 хвилин від початку руху має кутову швидкість, яка відповідає 120 об /хв. Визначити число обертів N, які зробив шків за 10 хвилин.

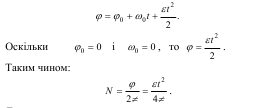Розв’язок. Число обертів N можна визначити, якщо відомий кут, на який повернувся шків за 10 хвилин.

Кут повороту тіла при рівноприскореному обертанні дорівнює:

Для визначення кутового прискорення ε скористаємося формулою для кутової швидкості при рівноприскореному обертанні тіла:

Дата добавления: 2014-11-16