Елементарна робота

У загальному випадку, коли матеріальна точка рухається по криволінійній траєкторії під дією змінної сили, вводиться поняття елементарної роботи.

Елементарна робота δA сили F на елементарному переміщенні dS (рис.9.2) ви значається наступним чином:

де Fτ - проекція сили F на тангенціальну вісь, яку направлено у бік переміщення

точки; dS - нескінченно мале переміщення точки.

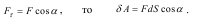Оскільки

Аналітичний вираз елементарної роботи сили. Робота сили на кінцевому переміщенні

Елементарну роботу сили можна представити у вигляді скалярного добутку векторів F і dr (рис.9.3):

де dr - вектор елементарного переміщення точки М.

Вираз елементарної роботи змінної сили через

проекції сили на осі декартових координат має вигляд:

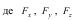
- проекції сили на координатні осі, а dx, dy, dz - проекції вектора елементарного переміщення на координатні осі.

Робота сили F на будь-якому кінцевому переміщенні M₀ M₁ визначається інтегралом:

Роботи сил тяжіння і пружності

Робота сили тяжіння дорівнює взятому зі знаком плюс або мінус добутку сили тяжіння на вертикальне переміщення точки її прикладення

де Р – сила тяжіння; h – вертикальне переміщення точки прикладення сили.

З цієї формули витікає, що робота сили тяжіння не залежить від форми траєкторії між початковою і кінцевою точками руху, а залежить тільки від відстані між горизонтальними площинами, які проходять через початкове та кінцеве положення точки.

Якщо початкова точка розташована вище кінцевої, то робота сили тяжіння додатня, у протилежному випадку – від’ємна.

Робота сили пружності дорівнює половині добутку коефіцієнта жорсткості пружини на різницю квадратів початкового та кінцевого видовжень (або стискань) пружини

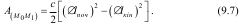
Робота сили пружності від’ємна у тому випадку, коли деформація збільшується, тобто коли

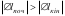Це відповідає переміщенню кінця пружини від положення рівноваги. Якщо, робота буде додатна. У цьому випадку кінець пружини переміщується до положення рівноваги.

Робота сили, що прикладена до тіла, яке обертається

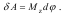Елементарна робота сили, прикладеної до будь-якої точки тіла, яке обертається навколо нерухомої осі, наприклад z, дорівнює добутку моменту сили відносно осі обертання на диференціал кута повороту:

У окремому випадку, коли момент сили є сталим, тобто M_z= const, робота дорівнює добутку моменту сили на кут повороту тіла: 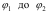Для того, щоб визначити роботу сили, яка діє на тіло при його повороті на кут від, необхідно проінтегрувати рівняння у цих межах, виразивши момент сили як функцію кута повороту:

9.2. Потужність сили

Потужністю називається величина, що визначає роботу, яку виконує сила за одиницю часу:

Цей вираз справедливий, якщо робота виконується рівномірно. У загальному випадку

Таким чином, потужність дорівнює добутку величини дотичної складової сили на швидкість руху.

Потужність виражається добутком обертального моменту на кутову швидкість.

Одиницею вимірювання потужності у системі СІ є Ватт

(1Вт = 1 Дж/с), у системі МкГС – 1 кГсм/с.

9.3. Контрольні запитання

Як визначається робота сталої за модулем і напрямком сили на прямолінійному переміщенні точки прикладення сили?

Як записується вираз для елементарної роботи у загальному вигляді?

Як визначається елементарна робота сили через проекції сили на осі координат?

Як вираховується робота сил тяжіння і пружності?

На яких переміщеннях робота сили тяжіння: додатня, від’ємна, дорівнює нулю?

У якому випадку робота сили пружності додатня і в якому від’ємна?

9.4. Порядок розв’язування задач на визначення роботи і потужності сили

При визначенні роботи необхідно розрізняти наступні випадки:

Прямолінійний рух під дією сталої сили; у цьому випадку застосовуються формули (9.2) та (9.3).

Прямолінійний рух під дією сили, яка є функцією відстані; у цьому випадку використовують формулу (9.5), яка, якщо спрямувати вісь х за траєкторією точки, приймає вигляд:

Криволінійний рух під дією сталої за модулем і напрямом сили; у цьому випадку можна використати формулу (9.4) або (9.5). Криволінійний рух під дією сили, що визначається функцією координат точки прикладення сили; у цьому випадку визначення роботи зводиться до обчислення криволінійного інтегралу за формулою (9.5).

Обертальний рух твердого тіла під дією сталого моменту або моменту, який є функцією кута повороту тіла; у цьому випадку для обчислення роботи використовуються формули (9.8) або (9.9).

Для обчислення потужності у залежності від характеруруху користуються формулою (9.11), якщо має місце прямолінійний, або криволінійний рух точки прикладення сили, або формулою (9.12) – у випадку обертального руху твердого тіла.

У всіх цих випадках перед обчисленням роботи або потужності необхідно зобразити всі зовнішні сили, які прикладенідо тіла або механічної системи, що розглядається.

9.5. Приклади розв’язування задач

Задача № 1

Визначити найменшу роботу А, яку необхідно виконати, щоб підняти на висоту h =5 м вантаж P=2 кН, пересуваючи

його по похилій площині, яка складає з горизонтом кут α =30⁰; коефіцієнт тертя f =0,5.

Розв’язок: Зобразимо вантаж у довільному положенні на похилій площині і покажемо всі діючі на нього сили (рис.9.4):

силу тяжіння P, силу тертя Fтр і нормальну реакцію N.

Робота, яка витрачається на піднімання вантажу на висоту h=5 м,

дорівнює сумі робот сили тертя вздовж довжини АВ та сили тяжіння на пере-

міщенні ВС точки її прикладення. Нормальна реакція роботи не виконує,

оскільки вона перпендикулярна переміщенню.

Обчислимо роботу сили тертя:

Робота сили тяжіння у нашому випадку від’ємна, оскільки вантаж рухається вгору, і дорівнює:

Задача № 2

Матеріальна точка М масою m рухається прямолінійно по горизонтальній площині за законом S=t⁴ під дією сили

F=12t² (рис.9.6). Визначити роботу цієї сили при переміщенні точки її прикладення з початкового положення (S₀ = 0) у положення, де S₁ = 4 м.

Розв’язок. Сила, яка діє на матеріальну точку М, змінюється з плином часу. Отже,

для визначення роботи цієї сили необхідно скористатися рівнянням (9.4):

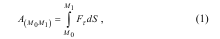
де F_τ - проекція сили на елементарне переміщення точки прикладення сили. У нашому випадку задана сила F співпадає за напрямком з переміщенням точки М, а роботу А необхідно вираховувати на перміщенні від S₀ до S₁.

Таким чином, рівняння (1) набуде вигляду:

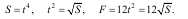Знайдемо залежність між силою F та переміщенням S, виключивши параметр t, який входить у вирази для значення сили та переміщення:

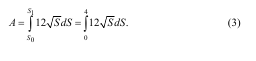Підставивши новий вираз для сили F у рівняння (2), одержимо:

Задача № 3

Шліфувальний камінь радіусом R= 30 см =0,3 м, робить n =120 об/хв. Потужність, яка споживається, дорівнює N=1,5 кВт =1500 Дж/с. Коефіцієнт тертя шліфувального каменю дорівнює f =0,2.

Визначити, з якою силою F притискає камінь деталь, яка шліфується?

Розв’язок. Деталь (рис.9.7) притискається до шліфувального каменю з силою F. Виникаюча при цьому сила тертя

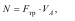F_тррозвиває потужність N, яка дорівнює спожитій потужності 1,5 кВт, тобто

де V_A - швидкість точки на ободі каменя, до якого прикладена

сила F. Сила тертя між каменем та деталлю складатиме:

кутова швидкість каменя буде:

а швидкість точки на ободі каменя дорівнює:

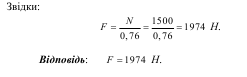
ТЕОРЕМА ПРО ЗМІНУ КІНЕТИЧНОЇ ЕНЕРГІЇ МЕХАНІЧНОЇ СИСТЕМИ

Зміст

10.1. Кінетична енергія механічної системи.

10.2. Визначення кінетичної енергії твердого тіла у різних випадках його руху.

10.3. Теорема про зміну кінетичної енергії механічної системи.

10.4. Контрольні запитання.

10.5. Порядок розв’язування задач на використання теореми про зміну кінетичної енергії механічної

системи.

10.6. Приклади розв’язування задач.

10.1. Кінетична енергія механічної системи

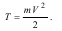Кінетичною енергією Т матеріальної точки називається скалярна додатня величина, яка дорівнює половині добутку маси точки на квадрат її швидкості:

Кінетичною енергією Т механічної системи називається арифметична сума кінетичних енергій усіх точок механічної системи:

Кінетична енергія системи не залежить від напрямків швидкостей точок. Кінетична енергія може дорівнювати нулю, якщо швидкості усіх точок системи дорівнюють нулю.

Кінетична енергія системи характеризує і поступальний, і обертальний рухи системи. Тому теоремою про зміну кінетичної енергії особливо часто користуються при розв’язуванні задач.

Одиницею кінетичної енергії у системі СІ є Джоуль (Дж).

10.2. Визначення кінетичної енергії твердого тіла у різних випадках його руху

10.2.1. Поступальний рух твердого тіла

При поступальному русі твердого тіла швидкості усіх його точок (у тому числі швидкість V_C центра мас тіла) у

кожний момент часу рівні між собою; тобто, для будь-якої точки V_k= V_С. Отже

Кінетична енергія твердого тіла при поступальному русі дорівнює половині добутку маси тіла М на квадрат швидкості його центра мас.

10.2.2. Обертальний рух твердого тіла

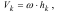Швидкість будь-якої точки твердого тіла, яке обертається з кутовою швидкістю ω, дорівнює

де h _k - відстань від точки до осі обертання.

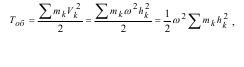Тоді кінетична енергія тіла визначається відповідно до залежності:

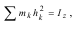Оскільки:

то

Отже кінетична енергія тіла при обертальному русі дорівнює половині добутку моменту інерції тілавідносно осі обертання на квадрат кутової швидкості тіла.

10.2.3. Плоскопаралельний рух твердого тіла

При плоскопаралельному русі швидкості усіх точок тіла в кожний момент часу розподілені так, начебто тіло обертається навколо осі, яка перпендикулярна до площини руху і яка проходить через миттєвий центр швидкостей Р. У цьому випадку кінетичну енергію тіла можна визначити за формулою:

де I_P - момент інерції тіла відносно осі, яка проходить через миттєвий центр швидкостей. Оскільки (згідно з теоремою Штейнера-Гюйгенса)

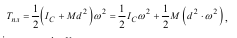де I_C - момент інерції відносно осі, яка проходить через центр мас тіла і паралельна миттєвій осі обертання, то

Таким чином, у випадку плоскопаралельного руху тіла кінетична енергія складається з кінетичних енергій оступального руху разом зі швидкістю центра мас і обертального руху навколо осі, яка проходить через центр мас перпендикулярно до площини руху.

10.3. Теорема про зміну кінетичної енергії механічної системи

Диференціальна форма

Диференціал кінетичної енергії механічної системи дорівнює сумі елементарних робіт усіх зовнішніх і внутрішніх сил, які діють на систему:

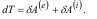
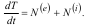Похідна за часом від кінетичної енергії механічної системи дорівнює сумі потужностей усіх зовнішніх і внутрішніх сил, які діють на систему:

Інтегральна форма

Зміна кінетичної енергії механічної системи при кінцевому переміщенні її з положення (1) в положення (2) дорівнює сумі робіт на цьому переміщенні усіх зовнішніх і внутрішніх сил, які діють на цю систему

Якщо механічна система незмінна, то сума робіт внутрішніх сил дорівнює нулю і теорема запишеться так:

10.4. Контрольні запитання

Що називається кінетичною енергією матеріальної точки?

Що називається кінетичною енергією механічної системи?

Як визначається кінетична енергія твердого тіла у випадку поступального руху?

Як визначається кінетична енергія твердого тіла при обертальному русі?

Як визначається кінетична енергія твердого тіла при плоскопаралельному русі?

Як формулюються теореми про зміну кінетичної енергії механічної системи?

Чи входять у рівняння, які виражають теорему про зміну кінетичної енергії системи, внутрішні сили цієї системи?

У якому випадку у рівняння, які виражають теорему про зміну кінетичної системи, не входять внутрішні сили?

Якщо дана ізольована від дії будь-яких зовнішніх сил система таким чином, що на її точки діють тільки внутрішні сили, то чи буде змінюватися кінетична енергія такої системи?

10.5. Порядок розв’язування задач на використання теореми про зміну кінетичної енергії механічної системи

Розв’язування задач за допомогою теореми про зміну кінетичної енергії в інтегральній формі рекомендується проводити у наступній послідовності:

а) зобразити на рисунку всі зовнішні сили системи;

б) вирахувати суму робіт усіх зовнішніх сил на переміщенні точок системи;

в) вирахувати кінетичну енергію системи матеріальних точок у початковому та кінцевому її станах;

г) користуючись результатами підрахунків за пунктами б) і в), записати теорему про зміну кінетичної енергії механічної системи і визначити шукану величину.

10.6. Приклади розв’язування задач

Задача № 1

Механізм еліпсографа (рис.10.1) складається з повзунів А і В вагою Р кожний, кривошипа ОС вагою 2Р, і лінійки АВ вагою 3Р. Кривошип ОС обертається навколо нерухомої осі О, яка перпендикулярна до площини креслення з кутовою швидкістю ω.

Визначити кінетичну енергію механізму еліпсографа, вважаючи, що лінійка АВ і кривошип ОС – однорідні тонкі стержні, а повзуни А і В – матеріальні точки, а також, що ОС=АС=СВ= l.

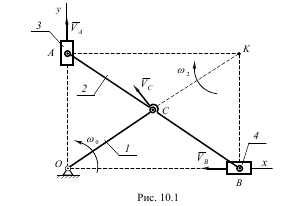
Розв’язок. Задана механічна система складається з чотирьох тіл: кривошипа 1, лінійки 2, повзунів 3 і 4. Кінетична енергія усієї системи дорівнює:

де T₁ - кінетична енергія кривошипа 1, T ₂ - кінетична енергія лінійки 2, T₃,T₄ - кінетична енергія повзунів 3 та 4. Кривошип ОС здійснює обертальний рух навколо нерухомої осі Оz, яка перпендикулярна до осі рисунка. В цьому випадку кінетична енергія тіла дорівнює

Лінійка 2 рухається плоскопаралельно. Її кінетична енергія дорівнює

де V_C - швидкість точки С, яка є центром мас лінійки 2,

ω₂ - кутова швидкість лінійки 2,

I_Cz - момент інерції лінійки відносно осі Сz, яка проходить через центр мас лінійки С.

Для визначення кутової швидкості ω₂лінійки 2 використаємо поняття миттєвого центра швидкостей. Як відомо, миттєвий центр швидкостей розташовано на перетині перпендикулярів до швидкостей двох точок тіла, що рухається плоскопаралельно. Тоді у нашому випадку його буде розташовано у точці К, і швидкість точки С визначиться:

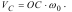З другого боку, точка С належить ланці 1, і її швидкість дорівнює

Тоді, враховуючи, що ОС=СК, отримаємо:

Момент інерції лінійки відносно осі z_С дорівнює:

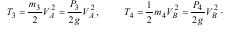Підрахуємо кінетичну енергію повзунів 3 і 4, які рухаються поступально:

Швидкості точок АВ можна визначити, враховуючи положення миттєвого центра швидкостей лінійки 2:

ЗАГАЛЬНЕ РІВНЯННЯ ДИНАМІКИ

Зміст

14.1. Загальне рівняння динаміки.

14.2. Порядок розв’язування задач на застосування загального рівняння динаміки.

14.3. Приклади розв’язування задач.

14.1. Загальне рівняння динаміки

Закони Ньютона установлені для вільної матеріальної точки і вільної матеріальної системи. Однак, частіше зустрічаються невільні системи. Ця обставина суттєво ускладнює використання законів Ньютона для розв’язування задач динаміки невільних механічних систем, а часто і зовсім не дозволяє розв’язувати такі задачі.

Необхідність розв’язування задач динаміки невільних механічних систем у зв’язку з їх важливим практичним значенням обумовила розробку ряду методів розв’язку таких задач. У цьому першорядне значення належить загальним принципам і загальним рівнянням механіки.

Із принципів раніше були розглянуті наступні.

Принцип Даламбера. Він полягає у тому, що у кожний момент часу зрівноважуються між собою діючі на “k”-ту точку невільної матеріальної системи активні сили F_k, реакції в’язей N_k і сили інерції Ф _k, які прикладені до цих точок. Цей принцип записується формулою 12.6:

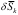
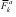Принцип можливих переміщень. Він у найбільш загальній формі установлює умови рівноваги невільних матеріальних систем і полягає у тому, що для рівноваги матеріальної системи, яка підкоряється ідеальним стаціонарним в’язям, необхідно і достатньо, щоб сума елементарних робіт, які здійснюються активними силами на можливих переміщеннях точок механічної системи, дорівнювала нулю:

Принцип можливих переміщень дає загальний метод розв’язування задач статики. З іншого боку, принцип Даламберадозволяє використовувати методи статики для розв’язування задач динаміки. Отже, застосовуючи ці два принципи одночасно, можна одержати загальний метод розв’язування задач динаміки, який має назву загального рівняння динаміки: при русі системи з ідеальними в’язями у кожний даний момент часу сума елементарних робіт усіх прикладених активних сил і усіх сил інерції на будь-якому можливому переміщенні системи буде дорівнювати нулю

14.2. Порядок розв’язування задач на застосування загального рівняння динаміки

Установити, рух якої невільної системи розглядається.

Визначити характер в’язей, які накладені на систему, ураховуючи властивість ідеальних в’язей.

Позначити активні сили, які діють на точки системи.

Визначити можливі переміщення системи.

Умовно прикласти до точок системи сили інерції і підрахувати їх величину.

Скласти суму робіт активних сил і сил інерції на установлених переміщеннях системи.

Із одержаного співвідношення знайти шукані величини.

Застосувати загальне рівняння динаміки до розв’язування задач необхідно у тому випадку, коли за умовою задачі за відомими активними силами необхідно визначити прискорення системи (лінійне або кутове), а також сили, які діють на точки системи.

14.3. Приклади розв’язування задач

Задача №1

Вантаж А вагою Р, опускаючись по похилій гладкій площині, яка складає з горизонтом кут α, призводить до обертання барабана В вагою Q з радіусом r за допомогою невагомої нитки, що не розтягується, (рис.14.1).

Визначити кутове прискорення барабана, якщо рахувати барабан однорідним круглим циліндром. Масою нерухомого блока С знехтувати.

Розв’язок. Дана невільна система складається з вантажу А і барабана В, сили тяжіння (активні сили) яких P і Q - задані. Зв’язком між вантажем і барабаном є невагома нитка, яка не розтягується. Зовнішніми в’язями по відношенню до системи є похила поверхня, а також підшипники O₁ і O₂.

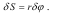Визначимо можливі переміщення системи. Для барабана можливим переміщенням буде кут повороту δϕ, для поступального руху вантажу А можливе переміщення S δ. Установимо залежність між величинами δϕ і S δ. При переміщенні вантажу вниз на величину S δ, нитка змотується з барабана на ту ж саму величину S δ, а барабан повернеться на кут δϕ. Тобто

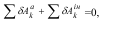Прикладемо до невільної механічної системи сили інерції. Якщо вантаж А опускається з прискоренням a, направленим униз по похилій поверхні, то сила інерції вантажу Ф направлена у протилежний бік. Момент сил інерції B_інM барабана направлений так, як показано на рисунку 14.1, у бік, протилежний кутовому прискоренню ε.

Складемо загальне рівняння динаміки системи у формі (14.3):

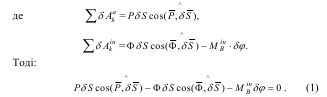
ε - кутове прискорення барабана.

Підставляючи усі ці дані у рівняння (2), одержимо:

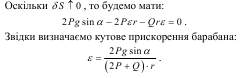
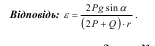
ТЕОРІЯ УДАРУ

Зміст

15.1. Явище удару. Основне рівняння теорії удару.

15.2. Удар тіла об нерухому перешкоду.

15.3. Прямий центральний удар двох тіл (удар куль).

15.4. Втрата кінетичної енергії при непружному ударі двох тіл.

15.5. Контрольні запитання.

15.6. Порядок розв’язування задач.

15.7. Розв’язування задач.

15.1. Явище удару. Основне рівняння теорії удару

З механічної точки зору явище удару характеризується тим, що швидкості точок механічної системи (твердого тіла) змінюються на кінцеву величину за дуже малий проміжок часу, який складає тисячні і менші частки секунди, за який відбувається удар. Оскільки при ударі кінцева зміна швидкостей відбувається за дуже малий проміжок часу, то прискорення, що виникають, будуть дуже великими, отже, при ударі діють і дуже великі сили.

Сили, які виникають під час удару і які діють, хоч і у дуже малий проміжок часу, на тіла, які стикаються, мають кінцеву величину і називаються ударними силами. Дуже малий проміжок часу, за який здійснюється удар, називається часом удару.

Імпульси ударних сил за час удару називаються ударними імпульсами.

Оскільки ударні сили дуже великі і за час удару змінюються від нуля до дуже великого значення, а потім знову падають до нуля, то в теорії удару за міру механічної взаємодії тіл, які стикаються, розглядаються не ударні сили, а їх ударні імпульси, які є кінцевими величинами.

Основне рівняння теорії удару для матеріальної точки випливає з теореми про зміну кількості руху матеріальної точки і має вигляд:

де V - швидкість точки на початку удару;

U - швидкість точки у кінці удару;

S - імпульс ударної сили.

Знаючи масу точки, її швидкість на початку удару і ударний імпульс, з рівняння (15.1) можна визначити швидкість точки після удару:

15.2. Удар тіла об нерухому перешкоду

Центральним ударом тіла об нерухому перешкоду називають такий удар, коли нормаль до поверхні тіла у точці його контакту з перешкодою проходить через центр мас тіла.

Якщо швидкість V центра мас тіла на початку удару спрямована за нормаллю n до перешкоди, то удар буде прямим, у іншому випадку косим.

Випадок прямого удару Після удару тіло (куля) набуває швидкості U, яка напра-

влена за нормаллю у протилежний бік (рис.15.1). У цьому випадку модуль

швидкості у кінці удару пропорційний модулю швидкості на початку удару:

де k - коефіцієнт відновлення під час удару.

Коефіцієнт відновлення k залежить від матеріалу тіла (кулі) та нерухомої поверхні і характеризує природу тіл, які стикаються. Значення коефіцієнта відновлення для різних тіл визначається експериментальним шляхом.

Розрізняють три випадки:

k = 0, і отже, швидкість після удару U = 0. Це абсолютно непружний удар;

k= 1, і отже, швидкість у кінці удару за модулем дорівнює швидкості на початку удару; такий удар називається абсолютно пружним;

0 < k<1, у цьому разі U <V. Це характеризує не зовсім пружний удар.

Знаючи масу тіла m, швидкість до удару і коефіцієнт відновлення, можна визначити ударний імпульс:

Випадок косого удару

У цьому випадку швидкість V центра мас тіла на початку удару

складає з нормаллю до поверхні кут αа

швидкість U у кінці удару кут β (рис.15.2).

У випадку, який розглядається, діючою на тіло (кулю) силою

буде нормальна реакція поверхні. Імпульс цієї реакції S.

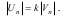Для нормальних складових швидкостей у відповідності з

рівнянням (15.3):

Таким чином, основні залежності для косого удару мають вигляд рис.(15.2)

Із співвідношень (15.5) можна знайти модуль і напрямок швидкості у кінці удару і ударний імпульс, якщо величини m, V, α і k відомі.

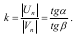Коефіцієнт відновлення при косому ударі є відношенням тангенса кута падіння α до тангенсу кута відбивання β

(рис.15.2):

Оскільки k <1, то β <α, тобто кут падіння завжди менший за кут відбивання.

15.3. Прямий центральний удар двох тіл (удар куль)

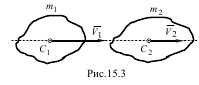Прямим центральним ударом двох тіл називається такий удар, при якому точка стикання тіл лежить на прямій, яка з’єднує їх центри мас, а швидкості центрів мас направлені вздовж цієї лінії (рис.15.3).

Швидкості тіл до удару позначені V₁ і V₂. Швидкості тіл

після удару позначені U₁ і U₂. Для випадку не

зовсім пружного удару залежність між швидкостями

V₁, V ₂, U₁ і U₂ має вигляд:

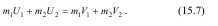Закон збереження кількості руху системи (тіл C₁ і C₂) запишеться у вигляді:

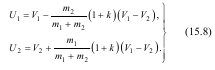Із рівнянь(15.6) і (15.7) одержуються алгебраїчні значення абсолютних швидкостей у кінці удару:

Ударний імпульс, що діє на тіла, які дотикаються, дорівнює:

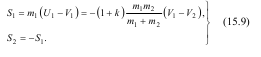
Абсолютно непружний удар (k =0)

У цьому випадку, коли

обидва тіла після удару рухаються з однаковими швидкостями. Діючі на тіла ударні імпульси дорівнюють:

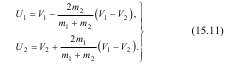Абсолютно пружний удар (k =1)

У цьому випадку:

Діючі на тіла ударні імпульси дорівнюють:

Якщо стикаються тіла з однаковою масою, то

Таким чином, у цьому випадку тіла обмінюються швидкостями.

15.4. Втрата кінетичної енергії при непружному ударі двох тіл.

Якщо удар не зовсім пружний, то тіла, які стикаються, не миттєво та не повністю відновлюють свої форми у кінці удару. Отже, частина кінетичної енергії, якою володіли ці тіла на початку удару, витрачається на залишкову їх деформацію, а також на нагрівання цих тіл.

Величина втраченої кінетичної енергії при абсолютно непружному ударі

(k = 0)визначається з виразу:

15.5. Контрольні запитання

У чому полягає характерна особливість явища удару?

Чому замість ударних сил у теорії удару фігурують ударні імпульси?

Як записати основне рівняння теорії удару для матеріальної точки?

Що називається коефіцієнтом відновлення?

У яких межах знаходяться числові значення коефіцієнта відновлення?

На що витрачається кінетична енергія при ударі?

Яка залежність між кутами падіння і відбивання при ударі об гладку нерухому поверхню?

Як визначається втрачена при ударі кінетична енергія у випадку:

- абсолютно непружного,

- непружного ударів?

15.6. Порядок розв’язування задач

Задачі про визначення швидкостей тіл, які стикаються при прямому центральному ударі.

Спрямувати вісь n уздовж лінії центрів мас тіл, що стикаються.

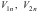Обчислити проекції початкових швидкостей тіл, які стикаються, на вісь n.

У випадку непружного удару вирахувати за формулою (15.10) проекції загальної швидкості на вісь n у кінці удару тіл, які стикаються.

У випадку пружного удару вирахувати проекції на вісь n швидкості за формулами (15.11) і (15.12).

Визначити швидкості обох тіл у кінці удару.

Вирахувати імпульс миттєвої (ударної) сили за формулою (15.9).

У випадку удару об нерухому площину можна скористатися наведеними формулами, якщо рахувати у них масу нерухомої площини нескінченно великою, а швидкість до удару рівною нулю, тобто

15.7. Приклади розв’язування задач

Задача №1

Важка кулька без початкової швидкості (рис.15.4) падає з висоти Н=1,5м і після удару об горизонтальну перешкоду піднімається на висоту h=0,8 м. Визначити коефіцієнт відновлення при ударі.

Розв’язок. У задачі розглядається випадок прямого удару у

перешкоду. За відомою формулою Галілея можна одержати

швидкість кульки на початку удару – V та після удару – U:

Відповідь: k =0,73.

Задача №2

Сталева куля вагою 2 PH =, падаючи з висоти 4 H = м, ударяється об сталеву плиту, яку розташовано горизонтально (рис.15.4).

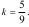Визначити ударний імпульс та середнє значення ударної реакції, якщо час удару становить τ =0,0002 с і коефіцієнт відновленняk

Розв’язок. У задачі розглядається центральний удар у нерухому перешкоду. Оскільки коефіцієнт відновлення 0 <k<1, то у даному випадку центральний удар є не зовсім пружним.

Для визначення ударного імпульсу S скористуємося залежністю (15.4):

де m – маса кулі,

V – швидкість кулі у момент початку удару.

Визначимо швидкість кулі у момент удару. При вільному падінні кулі з висоти H, його швидкість наприкінці падіння дорівнює

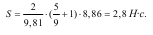Після підстановки у рівняння (1) значень m, k та V отримаємо:

Величина середньої ударної реакції N_CP визначимо з виразу:

Дата добавления: 2014-11-16