С. Г. Дробязко, В. С. Козлов 2 страница

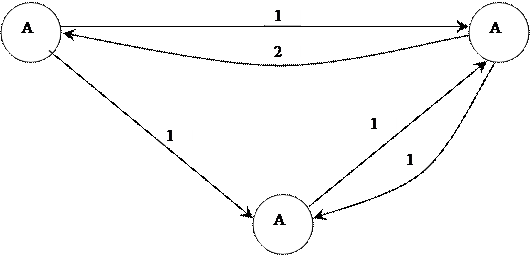
Пример. Задана матрица интенсивностей переходов непрерывной цепи Маркова. Составить размеченный граф со­стояний, соответствующий матрице ; составить систему диф­ференциальных уравнений Колмогорова для вероятностей состояний; найти предельное распределение вероятностей.

Дано:

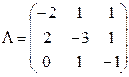
Решение: Однородная цепь Маркова с конечным числом состояний A₁,A₂,…,A_k характеризуется матрицей интенсивностей переходов

,

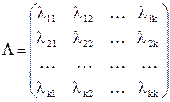где 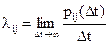- интенсивность перехода цепи Маркова из состояния A_i в состояние A_j;

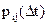- вероятность перехода A_i A_j за интервал времени .

Переходы системы из состояния в состояние удобно задавать с помощью размеченного графа состояний, на котором отмечаются дуги, соответствующие интенсивностям .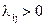

Составим размеченный граф состояний для заданной матрицы интенсивностей переходов.

Пусть - вектор вероятностей , нахождения системы в состоянии A_j в момент t. Очевидно, что 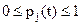и . Тогда по правилу дифференцирования векторной функции скалярного аргумента получим 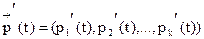. Вероятности 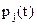удовлетворяют системе дифференциальных уравнений Колмогорова (СДУК), которая в матричной форме имеет вид

(6)

,

Если в начальный момент система находилась в состоянии A_j, то СДУК следует решать при начальных условиях

(7)

Совокупность СДУК (6) и начальных условий (7) однозначно описывает однородную цепь Маркова непрерывным временем и конечным числом состояний.

Составим СДУК для заданной цепи Маркова. Поскольку k=3, то j=1,2,3. Из соотношения (6) получим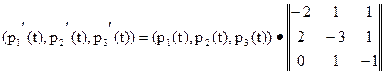

Отсюда будем иметь:

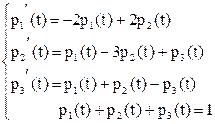
Последнее условие называется нормировочным.

Распределение 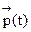вероятностей по состояниям называется стационарным, если оно не меняется с течением времени, то есть 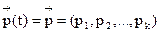, где p_j=const, j=1,2,…,k.

Отсюда 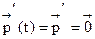. Тогда из СДУК (6) получаем систему для нахождения стационарного распределения 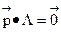, где .

Для данной задачи из СДУК будет иметь

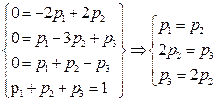
Из нормировочного условия получим

Ответ: предельное распределение имеет вид .

Пример. Определить, существует ли стационарный режим для марковского случайного процесса, размеченный граф состояний которого изображен на рисунке. Если стационарный режим существует, то найти стационарное распределение вероятностей.

Указание. Проведите классификацию состояний системы и примените следствия из теоремы Маркова.

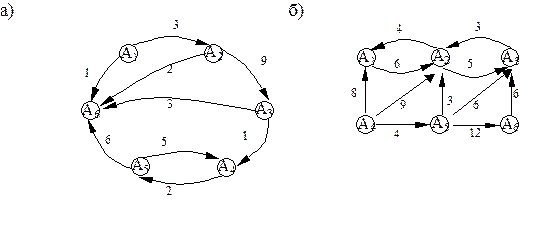
а) Состояние 6 - существенное. Остальные - несущественные состояния. Поэтому единственное стационарное распределение совпадает с предельным.

Для несущественных состояний предельные вероятности равны нулю. Учитывая, что сумма всех вероятностей = 1 получим искомое стационарное распределение:

б) Несущественные состояния 1, 2, 6. Состояния 3, 4, 5 - существенные сообщающиеся поэтому единственное стационарное распределение совпадает с предельным.

Приравнивая к каждую из строк-уравнений к 0 и учитывая, что сумма вероятностей = 1 получим:

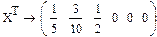
11.Процесс гибели и размножения

Процессом гибели и размножения называется марковская цепь, размеченный граф состояний которой изображен на рис. 3. Здесь l₀, l₁, …,l_k-1— интенсивности переходов си­стемы из состояния в состояние слева направо; m₁, m₂,…, m_k —

Рис. 3

интенсивности переходов справа налево. Очевидно, все со­стояния A₀, A₁,..., A_k являются существенными сообщающи­мися состояниями. Следовательно, в силу теоремы 2 сущест­вует предельное распределение вероятностей состояний, ко­торое имеет вид:

p₀ = ;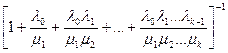

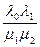p₁ = p₀; p₂ = p₀; …; p_k = 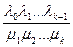p₀. (11)

12.Системы массового обслуживания и их классификация.

Математический аппарат для изучения закономерностей функционирования систем, удовлетворяющих массовый спрос, и образования очередей в такого рода системах называется теорией массового обслуживания.

Методы теории массового обслуживания все более широ­ко применяются на транспорте для расчета рациональной ор­ганизации подачи вагонов под разгрузку и погрузку, для рас­чета мощностей пунктов текущего ремонта вагонов, для вы­бора рационального числа кассовых аппаратов на вокзалах и станциях метрополитена. Поэтому современному инженеру железнодорожного транспорта необходимо знать основы тео­рии массового обслуживания.

Поступление заявки в СМО назовем событием. Последо­вательность событий, состоящих в поступлении заявок в СМО, назовем входящим потоком заявок. Последовательность собы­тий, состоящих в выходе заявок из СМО, назовем выходящим потоком заявок.

В зависимости от поведения заявки в СМО различают СМО с отказами и СМО с очередью (или ожиданием). В СМО с отказами заявка, поступившая в момент занятости всех каналов, получает отказ и покидает СМО. В СМО с оче­редью (или ожиданием) заявка, поступившая в момент за­нятости всех каналов, становится в очередь и ожидает осво­бождения одного из каналов обслуживания.

Возможны СМО смешанного типа. Например, СМО с ог­раниченной очередью. В такой СМО заявка становится в оче­редь при занятости всех каналов, если очередь невелика, скажем, не достигла длины т. Если все т мест в очереди за­няты, заявка покидает СМО. К СМО смешанного типа отно­сятся СМО с ограниченным временем ожидания. Заявка, по­ступившая в момент занятости всех каналов, становится в очередь, но может уйти из СМО необслуженной, если время ожидания слишком велико.

СМО с очередью (или с ожиданием) могут быть открыто­го и замкнутого типа. В открытых СМО интенсивность по­ступающего на нее потока заявок не зависит от состояния самой СМО, так как круг «клиентов» (поступающих заявок) практически не ограничен. Примерами таких СМО являются вокзальные кассы, метрополитен, телевизионные ателье больших городов и т. д. В СМО с очередью замкнутого типа об­служивается ограниченный круг «клиентов», поэтому интен­сивность потока заявок существенно зависит от состояния си­стемы. Примерами таких СМО являются различные ремонт­ные системы в автопарках, цехах и т. д.

СМО с очередью и смешанного типа различаются также по дисциплине обслуживания; обслуживаются ли заявки в порядке поступления, или в случайном порядке, или есть заявки, которые обслуживаются вне очереди (СМО с приорите­том).

13. Марковские системы массового обслуживания

Для задания СМО необходимо задать вероятностные ха­рактеристики времени обслуживания одной заявки. Обозна­чим это время через T _обсл. Величина T _обсл является случай­ной. Во многих задачах теории массового обслуживания закон распределения времени обслуживания предполагается пока­зательным, т. е.

F(t) = P(T _обсл < t) = 1 - e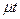^- . (15)

Параметр этого распределения l есть величина, обратная среднему времени обслуживания, т. е.

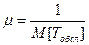. (16)

Часто m называют интенсивностью потока обслуживания.

При этом под потоком обслуживания понимается поток зая­вок, обслуживаемых одна за другой одним непрерывно заня­тым каналом. Если Т_обсл представляет собой случайную ве­личину, имеющую показательное распределение, то поток об­служивания является простейшим.

Таким образом, предположение о показательном законе распределения времени обслуживания и интервала времени между двумя последовательными поступлениями заявок иг­рает исключительную роль в теории массового обслуживания, так как упрощает аналитическое исследование СМО, сводя его к исследованию цепей Маркова.

14. Показатели эффективности систем массового обслуживания

Обычно в теории массового обслуживания интересуются предельными средними характеристиками системы, которые называют показателями эффективности СМО. В качестве по­казателей эффективности могут рассматриваться следующие:

А — среднее число заявок, обслуживаемое СМО в еди­ницу времени. Эту характеристику называют абсолютной пропускной способностью СМО.

Q - вероятность обслуживания поступившей заявки или относительная пропускная способность СМО. Очевидно, Q = .

р _отк — вероятность отказа, т. е. вероятность того, что по­ступившая заявка не будет обслужена, Р_отк = 1—Q.

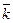— среднее число занятых каналов.

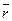— среднее число заявок в очереди, если она есть.

— среднее число заявок в СМО (имеются в виду все заявки, как обслуживаемые, так и ожидающие очереди, ес­ли они есть).

— среднее время пребывания заявки в очереди.

— среднее время пребывания заявки в СМО, как в очереди, если она есть, так и под обслуживанием.

Выбор показателей эффективности СМО зависит от типа СМО. Например,

абсолютная пропускная способность А яв­ляется основной характеристикой обслуживания в СМО с от­казами;

для СМО с неограниченной очередью абсолютная пропускная способность А = l и не является поэтому новым показателем.

15.Замкнутые системы массового обслуживния

Задача. Автоматизированная система управления АСУ продажей железнодорожных билетов состоит из двух параллельно работающих ЭВМ. При выходе из строя одной ЭВМ АСУ продолжает нормально функционировать за счет работы другой ЭВМ. Поток отказов каждой ЭВМ простей­ший. Среднее время безотказной работы одной ЭВМ равно 10 суткам. При выходе из строя отказавшую ЭВМ начинают ремонтировать. Время ремонта ЭВМ распределено по пока­зательному закону и в среднем составляет 2 суток. В начальный момент обе ЭВМ исправны. Найти: 1) вероятность того, что обе ЭВМ исправны, 2) среднее число работающих ЭВМ, 3) среднюю производи­тельность АСУ, если при исправности хотя бы одной ЭВМ ее производительность равна 100%, а при отказе обеих ЭВМ продажа билетов производится вручную, обеспечивая 30% общей производительности АСУ.

Решение. 1) найдем вероятность того, что обе ЭВМ исправны.

Обозначим состояния АСУ по числу вышед­ших из строя ЭВМ: A₀ — обе ЭВМ исправны; А₁ — одна ис­правна, одна ремонтируется; А₂ — обе ЭВМ ремонтируются. Так как потоки отказов и восстановления ЭВМ являются про­стейшими, то их интенсивности вычисляются по формулам (14) и (16):

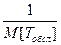l = = 0, 1 (отказов/сутки); m = =0,5 (восстановления/сутки)

Размеченный граф состояний изображен на рис. 5.

l₀ = 1/5 l₁ = 1/10

А₀ А₁ А₂

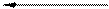m₁ = 1/2 m₂ = 1

рис. 5

По­скольку в состоянии A₀ работают две ЭВМ, каждая из которых может отказать с интенсивностью l = 1/10, то АСУ перехо­дит из состояния а₀ в состояние А₁ с интенсивностьюl₀ =2(1/10) = 1/5; переход А₁®А₂ происходит с интенсивностью l₁ = 1/10.

Из состояния А₂ в состояние А₁ система перехо­дит с интенсивностью m₂ = 2 m = 2 (1/2) =1,так как восстанав­ливаются две ЭВМ; переход А₁® А₂ происходит с интенсив­ностью m₁ = m = 1/2. Полученный граф состояний является графом процесса гибели и размножения с числом состояний k + 1 = 3, так как k=2. Воспользуемся формулами (11) для вычисления пре­дельного распределения вероятностей

p₀ = 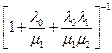= = 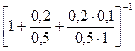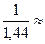0,694.

p₁ = 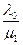p₀ = 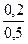0,694» 0,278;

p₂ = 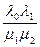p₀ = 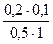0,694» 0,028.

Вычислим p₀ + p₁ +p₂ =0,694+0,278+0,028=l, что и следова­ло ожидать, так как система может находиться только в одном из трех возможных состояний А₀,, А₁, А₂.

2) найдем среднее число работающих ЭВМ.

`m = 2 p₀ + p₁ = 2 (0,694)+ 0,278 = 1,666

3) найдем среднюю производи­тельность АСУ.

Средняя производи­тельность АСУ в установившемся режиме составит

100% (p₀+p₁) +30%p2 = 100% (0,694+0,278) +30% • 0,028 = =98,04%.

Расчет показывает, что параллельная работа всего двух ЭВМ обеспечивает достаточно высокую (98,04% от номинальной) производительность АСУ. Следовательно, нет необходимости повышать производительность системы за счет, например, присоединения третьей ЭВМ.

51-60. Вход на станцию метрополитена оборудован системой из k турникетов.

При выходе из строя одного из турникетов остальные продолжают нормально

функционировать. Вход на станцию перекрывается, если выйдут из строя все турникеты.

Поток отказов каждого турникета - простейший, среднее время безотказной работы одного турникета t часов. При выходе из строя каждый турникет начинает сразу ремонтироваться. Время ремонта распределено по показательному закону и в среднем составляет s часов. В начальный момент все турникеты исправны. Найти среднюю пропускную способность системы турникетов в процентах от номинальной, если с выходом из строя каждого турникета система теряет (100/k)% своей номинальной пропускной способности.

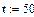
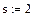
Найдем интенсивности и коэффициент r:

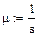
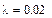
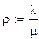
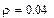
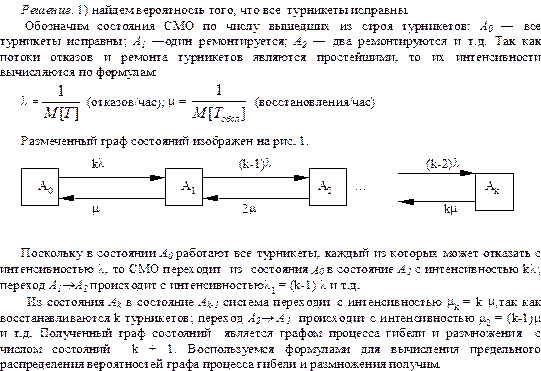
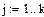
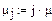
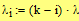
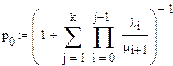
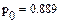
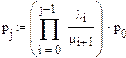
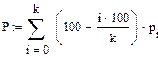
Расчет показывает, что параллельная работа 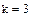турникетов обеспечивает достаточно высокую пропускную способность. Следовательно, нет необходимости увеличивать количество турникетов

16.Открытые системы массового обслуживания с простейшим входящим потоком и показательным временем обслуживания

Здесь рассматриваются СМО, у которых, входящий поток пуассоновский, а время обслуживания — показательное.

Многоканальная система массового обслуживания с ограниченной очередью

l l … l l l … l l

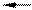
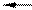
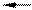
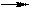
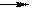А₀ А₁ А_k А_k+1 А_k+m-1 А_k+m

m 2m … km km km … km km

Рис. 6

Пусть СМО содержит k каналов, число мест в очереди – m (длина очереди), входящий поток заявок имеет интенсивность l, поток обслуживания заявки одним каналом имеет интенсивность m. Будем нумеровать состояния СМО по числу занятых каналов:

А₀— все каналы свободны; А₁ — один канал занят;......; A_i - i каналов занято, (k—i) каналов свободны;......; A_k— все каналы заняты; A_k+1— все каналы заняты, одна заявка в очереди; …; A_k+m— все каналы заняты, m заявок в очереди.

Размеченный граф состояний имеет вид, представленный на рис.6. Сравнивая рисунки 6 и 3, приходим к выводу, что граф на рис. 6 является графом процесса гибели и размножения, для которого:

l_i = l, m_i = m. (18)

Тогда предельное распределение вероятностей состояний можно вычислить по формулам (11). Обозначая через (коэффициент загрузки системы), с учетом соотношений (18) из (11) получим:

p₀ = ;

p₁ = 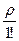p₀; p₂ = p₀; …; p_k = p₀; p_k+1 = 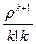p₀; …; p_k+m = 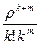p₀. (19)

Обозначим . Применяя формулу суммы ряда геометрической прогрессии, получим:

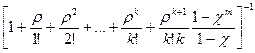p₀ = (20)

С помощью формул (19), (20) вычисляются показатели эффективности СМО:

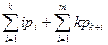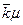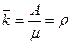А = ()m = = l(1 – p_k+m); Q = = 1 – p_k+m; P_отк = 1 – Q = p_k+m; (1 – p_k+m); ; (21)

Для открытых СМО справедливы соотношения:

= , = и 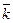= 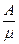. (17)

где l — интенсивность потока заявок, m — интенсивность потока обслуживания. Формулы (17) справедливы только в том случае, когда входящий поток заявок и поток обслужи­вания стационарны.

(Первая и вторая формулы называются формулами Литтла.)

Рассмотрим частные случаи:

1. Многоканальная система массового обслуживания с отказами (задача Эрланга).

Пусть m = 0, т.е. очередь не допускается, если все каналы обслуживания заняты, то заявка покидает СМО. Из формул (20), (21) получим:

p₀ = ;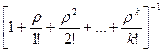

p₁ = 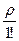p₀; p₂ = p₀; …; p_k = p₀. (22)

Формулы (22) называются формулами Эрланга.

А = l(1 – p_k); Q = 1 – p_k; P_отк = p_k; (1 – p_k); (23)

Задача 4. Диспетчерская служба имеет 5 линий связи. Поток вызовов простейший с интенсивностью l=0,8 вызовов в минуту. Среднее время переговоров с диспетчером состав­ляет t = 3 мин. Время переговоров распределено по показатель­ному закону. Найти 1) абсолютную и относительную пропуск­ные способности диспетчерской службы; 2) вероятность отказа; 3) среднее число занятых каналов. Определить, сколько линий связи должна иметь диспетчерская служба, чтобы вероят­ность отказа не превышала a = 0,01?

Решение. Находим интенсивность потока обслуживания m = 1/ M[T_обсл] = 1/3 разговора в минуту. Коэффициент загрузки СМО составляет r = = = 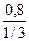2,4. Из формул (22) при k = 5 имеем:

p₀= 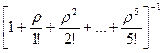= [10,629]^-1 0,094;

p₅ =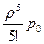
=

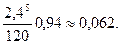
Находим по формулам (23):

а) абсолютная пропускная способность:

А = l(1—р₅) 0,8 (1—0,062) 0,8.0,938 0,750.

(следовательно, СМО обслуживает в среднем 0,75 заявки в минуту);

Дата добавления: 2014-11-16