Основное уравнение динамики при поступательном движении тела

Совокупность материальных точек, связанных между собой силами взаимодействия, называется механической системой.

Основы динамики системы материальных точек

Любое материальное тело в механике рассматривается как меха­ническая система, образуемая совокупностью материальных точек.

Из определения механической системы следует, что движение каждой из точек, входящих в систему, зависит от движения осталь­ныхточек.

Силы, действующие на точки системы, делятся на

· внешние и

· внутренние.

Силы взаимодействия между точками этой системы называют внутренними.

К внешним силам относятся силы, действу­ющие со стороны точек, не входящих в эту систему.

Примерами внешних сил являются сила тяжести, сила давления, сила трения и др.

К внутренним силам относятся силы упругости.

Движение механической системы зависит не только от внешних сил, но и от суммарной массы системы

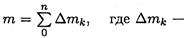масса отдельных точек механической системы.

Движение системы зависит и от положения центра масс систе­мы — условной точки, в которой сосредоточена вся масса тела. Обыч­но считают, что в центре масс приложены все внешние силы.

Движение центра масс определяет движение всей системы толь­ко при поступательном движении, при котором все точки тела дви­жутся одинаково.

Для определения движения тела (системы материальных точек) можно использовать второй закон динамики

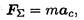
где т — суммарная масса тела; а_с — ускорение центра масс тела.

В поле земного притяжения центр масс совпадает с центром тяжести.

Основное уравнение динамики вращающегося тела

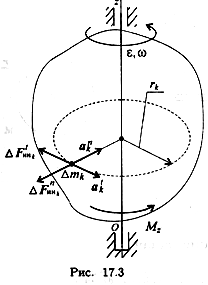
Пусть твердое тело под действием внешних сил вращается во­круг оси Oz с угловой скоростью ω (рис. 17.3).

Рассматривая твердое тело как механическую систему, разобьем ее на множество материальных точек с массами Δm_k. Каждая точ­ка движется по окружности радиуса r_k c касательным ускорением а_k^t = εr_k и нормальным ускорением

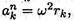где ε — угловое уско­рение.

Используем для каждой точки принцип Даламбера и приложим силы инерции:

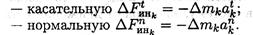
Система сил, действующих на точку, по принципу Даламбера, находится в равновесии.

Поэтому алгебраическая сумма моментов относительно оси вра­щения должна быть равна нулю:

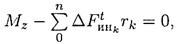
где Mz — момент внешних сил.

Моменты нормальных сил инерции F_инkⁿ равны нулю, т. к. силы пересекают ось z. Силы, направленные по касательной к окружно­сти, равны

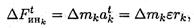
где ε — общая величина, угловое ускорение тела.

Подставив значение силы в формулу для определения моментов, получим

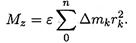
Величина

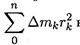
называется моментом инерции тела относи­тельно оси вращения и обозначается

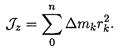
В результате получим выраже­ние основного уравнения динамики вращающего тела:

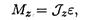
где Mz — сумма моментов внешних сил относительно оси; ε — угло­вое ускорение тела.

Момент инерции тела в этом выражении определяет меру инертности тела при вращении.

По выражению для момента инерции можно определить, что единица измерения этой величины в системе СИ [Jz\ = [тг2] = кг-м2.

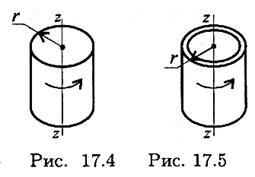
Видно, что значение момента инерции зависит от распределе­ния массы относительно оси вращения: при одинаковой массе момент инерции больше, если основная часть массы расположена дальше от оси вращения. Для увеличения момента инерции используют колеса со спицами и отверстиями.

Дата добавления: 2014-11-16