
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры решения задач. 1 страница
|
|
|
|
R и индуктивностью L
Обладающей сопротивлением
Поля через площадку S
где 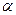 — угол между вектором
— угол между вектором  и
и
нормалью к площадке.
Закон электромагнитной индукции  ,
,
где N — число витков контура.
Потокосцепление контура с током 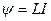 ,
,
где L — индуктивность контура.
Электродвижущая сила самоиндукции  .
.
Индуктивность соленоида 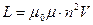 ,
,
где V — объем соленоида
n — число витков на единицу длины соленоида
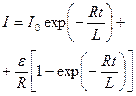 Мгновенное значение силы тока в цепи,
Мгновенное значение силы тока в цепи,
.
Энергия магнитного поля  .
.
Объемная плотность энергии магнитного поля  .
.
Пример 18. Три точечных заряда Q1= Q2= Q3=1 нКл расположены в вершинах равностороннего треугольника. Какой заряд Q4 нужно помесить в центр треугольника, чтобы указанная система находилась в равновесии.
 Решение. Все три заряда, расположенные по вершинам треугольника, находятся в одинаковых условиях. Поэтому достаточно выяснить, какой из зарядов, например Q1, находился в равновесии. Заряд Q1 будет находиться в равновесии, если векторная сумма действующая на него сил равна нулю (рис. 6):
Решение. Все три заряда, расположенные по вершинам треугольника, находятся в одинаковых условиях. Поэтому достаточно выяснить, какой из зарядов, например Q1, находился в равновесии. Заряд Q1 будет находиться в равновесии, если векторная сумма действующая на него сил равна нулю (рис. 6):
|
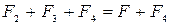 =0, (1)
=0, (1)
|
равнодействующая сил F2 и F3.
|
 F- F4=0, откуда F= F4. Выразим в последнем равенстве F
F- F4=0, откуда F= F4. Выразим в последнем равенстве F
через F2 и F3 и учитывая, что F2= F3, получим

Применив закон Кулона и имея в виду, что Q1= Q2= Q3, найдем
 ,
,
откуда
 . (2)
. (2)
Из геометрических построений в равностороннем треугольнике следует, что
 , cos α =cos 600=1/2.
, cos α =cos 600=1/2.
С учетом этого формула (2) примет вид
 .
.
Подставим числовые значения
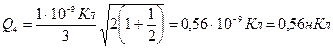
Пример 19. Два заряда 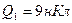 и
и 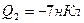 расположены в вершинах равностороннего треугольника со стороной
расположены в вершинах равностороннего треугольника со стороной  Определить напряженность и потенциал электрического поля в третьей вершине треугольника.
Определить напряженность и потенциал электрического поля в третьей вершине треугольника.
Р е ш е н и е. 1.Напряженность электрического поля в точке A (рис. 7) является геометрической (т. е. векторной) суммой напряженностей  и
и  полей, создаваемых зарядами
полей, создаваемых зарядами  и
и 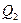 соответственно:
соответственно:

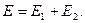
Модуль результирующий напряженности может быть найден по теореме косинусов как диагональ параллелограмма, построенного на векторах  и
и 
 (1)
(1)
 Напряженность электрического поля точечного заряда выражается формулой
Напряженность электрического поля точечного заряда выражается формулой
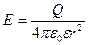 (2)
(2)
где Q – заряд, создающий поле; 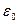 - электрическая постоянная;
- электрическая постоянная; 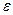 - диэлектрическая проницаемость среды; r – расстояние от расчётной точки поля до заряда, его создающего.
- диэлектрическая проницаемость среды; r – расстояние от расчётной точки поля до заряда, его создающего.
Так как 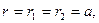 то имеем
то имеем

 (3)
(3)
Поскольку  преобразуем:
преобразуем:
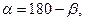
 (4)
(4)
Подставив (3) и (4) в (1), получим
 (5)
(5)
Выразим числовые значения величин в СИ: 
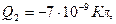
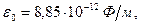
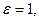

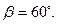
Проверим формулу (5):

Подставим в формулу (5) числовые данные и вычислим

Примечание. В расчётную формулу (5) подставлены модули зарядов, поскольку их знаки учтены при выводе этой формулы.
2. Потенциал электрического поля в точке А равен алгебраической сумме потенциалов  и
и 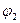 полей, создаваемых зарядами
полей, создаваемых зарядами  и
и 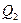 соответственно:
соответственно:
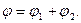 (6)
(6)
Потенциал поля точечного заряда выражается формулой
 (7)
(7)
В формуле (7) обозначения те же, что и в формуле (2). Подставив (7) в (6) и учитывая, что 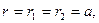 получим
получим
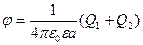 (8)
(8)
Подставив числовые значения величин в (8) и вычислим:
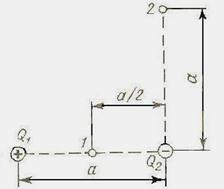

Пример 20. Электрическое поле создается двумя зарядами Q1= 4мкКл и Q2=-2 мкКл, находящимися на расстоянии а=0,1 м друг от друга. Определить работу А1,2 сил поля по перемещению заряда Q=50 нКл из точки 1 в точку 2 (рис.8)
Решение. Для определения работы А1,2 сил поля воспользуемся соотношением
|

Применяя принцип суперпозиции электрических полей, определим потенциалы φ1 и φ2 точек 1 и 2 поля:
 ; с.
; с.

Тогда
 ,
,
или
 .
.
Проверим, даст ли правая часть равенства единицу работы (Дж):

Подставим числовые значения физических величин и произведем вычисления:

Пример 21. Определить ускоряющую разность потенциалов U, которую должен пройти в электрическом поле электрон, обладающий скоростью υ1=106 м/с, чтобы скорость его возросла в n=2 раза.
Решение. Ускоряющую разность потенциалов можно найти, вычислив работу А сил электростатического поля. Эта работа определяется произведением элементарного заряда е на разность потенциалов U:

 (1)
(1)
 Работа сил электростатического поля в данном случае равна изменению кинетической энергии электрона:
Работа сил электростатического поля в данном случае равна изменению кинетической энергии электрона:

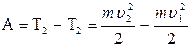 , (2)
, (2)
 где Т1 и Т2- кинетическая энергия электрона до и после прохождения ускоряющего поля; m- масса электрона; υ1 и υ2- начальная и конечная скорость его.
где Т1 и Т2- кинетическая энергия электрона до и после прохождения ускоряющего поля; m- масса электрона; υ1 и υ2- начальная и конечная скорость его.
Приравняв правые части равенства (1) и (2), получим
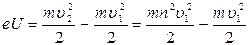 ,
,
где  .
.
Отсюда искомая разность потенциалов
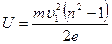 .
.
Произведем вычисления:
 .
.
Пример 22. Конденсатор емкостью С1=3 мкФ был заряжен до разности потенциалов U1=40 В. После отключения от источника тока конденсатор соединили параллельно с другим незаряженным конденсатором емкостью С2=5 мкФ. Какая энергия W израсходуется на образование искры в момент присоединения второго конденсатора?
Решение. Энергия, израсходованная на образование искры,
 , (1)
, (1)
где W1- энергия, которой обладал первый конденсатор до присоединения к нему второго конденсатора; W2- энергия, которую имеет батарея, составленная из двух конденсаторов.
Энергия заряженного конденсатора определяется по формуле
 , (2)
, (2)
где С- емкость конденсатора или батареи конденсаторов.
Выразив в формуле (1) энергии W1 и W2 по формуле (2) и приняв во внимание, что общая емкость параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов, получим
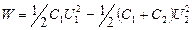 , (3)
, (3)
где U2- разность потенциалов на зажимах батареи конденсаторов.
Учитывая, что заряд после присоединения второго конденсатора остался прежним, выразим разность потенциалов U2 следующим образом:
 . (4)
. (4)
Подставив выражение U2 в (3), найдем

 ,
,
 или
или

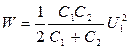 .
.
 Произведем вычисление:
Произведем вычисление:

 .
.
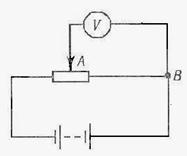 Пример 23. Потенциометр сопротивлением R=100 Ом подключен к батарее с ЭДС ε=150В и внутренним сопротивлением Ri=50 Ом. Определить: 1) показание вольтметра сопротивлением Rv=500 Ом, соединенного с одной из клемм потенциометра и подвижным контактом, установленным посередине потенциометра; 2) разность потенциалов междутеми же точками потенциометра при отключении вольтметра.
Пример 23. Потенциометр сопротивлением R=100 Ом подключен к батарее с ЭДС ε=150В и внутренним сопротивлением Ri=50 Ом. Определить: 1) показание вольтметра сопротивлением Rv=500 Ом, соединенного с одной из клемм потенциометра и подвижным контактом, установленным посередине потенциометра; 2) разность потенциалов междутеми же точками потенциометра при отключении вольтметра.
Решение. 1. Показание вольтметра, подключенного к точкам А и В (рис. 9), определим по формуле

 ,
,
 где R1- сопротивление, параллельно соединенных вольтметра и половины потенциометра; I1- суммарная сила тока в ветвях этого соединения (она равна силе тока в неразветвленной части цепи).
где R1- сопротивление, параллельно соединенных вольтметра и половины потенциометра; I1- суммарная сила тока в ветвях этого соединения (она равна силе тока в неразветвленной части цепи).
 Силу тока I1 найдем по закону Ома для полной цепи:
Силу тока I1 найдем по закону Ома для полной цепи:

 , (1)
, (1)
 где Re сопротивление внешней цепи. Это сопротивление есть сумма двух сопротивлений:
где Re сопротивление внешней цепи. Это сопротивление есть сумма двух сопротивлений:

 . (2)
. (2)
 Сопротивление R1 найдем по формуле параллельного соединения проводников
Сопротивление R1 найдем по формуле параллельного соединения проводников 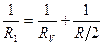 ,откуда
,откуда

 .
.
 Подставив в (1) выражение Re по (2), найдем
Подставив в (1) выражение Re по (2), найдем

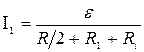 .
.
 В данном случае решение задачи в общем виде было бы громоздким. Поэтом удобно вычисление величин провести раздельно:
В данном случае решение задачи в общем виде было бы громоздким. Поэтом удобно вычисление величин провести раздельно:

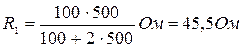 ;
;

 ;
;

 .
.
 2. Разность потенциалов между точками А и В при отключенном вольтметра равна произведению силы тока I2 на половину сопротивления потенциометра:
2. Разность потенциалов между точками А и В при отключенном вольтметра равна произведению силы тока I2 на половину сопротивления потенциометра:

 , (3)
, (3)
 где I2 - сила тока в цепи при отключенном вольтметре. Ее определим по формуле
где I2 - сила тока в цепи при отключенном вольтметре. Ее определим по формуле

 .
.

 Подставив выражение I2 в (3), найдем
Подставив выражение I2 в (3), найдем

 .
.
 Произведем вычисления:
Произведем вычисления:

 .
.
Пример 24. Сила тока в проводнике сопротивлением R=20 Ом нарастает в течение времени Δt=2 с по линейному закону от I0=0 до I= 6 А (рис 10). Определить теплоту Q1, выделившуюся в этом проводнике за первую секунду, и Q2- за вторую, а также найти отношение Q2/ Q1
Решение. Закон Джоуля- Ленца в виде 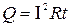 справедлив для постоянного тока (I=const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде
справедлив для постоянного тока (I=const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде


 . (1)
. (1)
 Здесь сила тока I является некоторой функцией времени. В данном случае
Здесь сила тока I является некоторой функцией времени. В данном случае

 , (2)
, (2)
 где k-коэффициент пропорциональности, характеризующий скорости изменения силы тока:
где k-коэффициент пропорциональности, характеризующий скорости изменения силы тока:
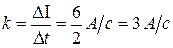 .
.
С учетом (2) формула (1) примет вид
 . (3)
. (3)
Для определения теплоты, выделившейся за конечный интервал времени Δt, выражение (3) надо проинтегрировать в пределах от t1 и t2:
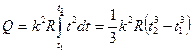 .
.
Произведем вычисления:
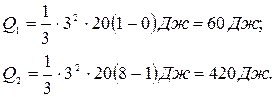

 Следовательно,
Следовательно,

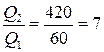 ,
,
 т.е. за вторую секунду выделится теплоты в семь раз больше, чем за первую.
т.е. за вторую секунду выделится теплоты в семь раз больше, чем за первую.
Пример 25. Два параллельных бесконечно длинных провода D и С, по которым текут в одном направлении электрические токи силой I=60 А, расположены на расстоянии d=10 см друг от друга. Определить магнитную индукцию В поля, создаваемого проводниками с током в точке А (рис. 11), отстоящей от оси одного проводника на расстоянии r1 = 5 см, от другого —r2 = 12 см.
 Решение. Для нахождения магнитной индукции В в точке А воспользуемся принципом суперпозиции магнитных полей. Для этого определим направления магнитных индукции B1 и B2 полей, создаваемых каждым проводником с током в отдельности, и сложим их геометрически:
Решение. Для нахождения магнитной индукции В в точке А воспользуемся принципом суперпозиции магнитных полей. Для этого определим направления магнитных индукции B1 и B2 полей, создаваемых каждым проводником с током в отдельности, и сложим их геометрически:
В=В1 + В2.
Модуль вектора В может быть найден по теореме косинусов:
 , (1)
, (1)
где α — угол между векторами В1 и В2.
Магнитные индукции B1 и В2 выражаются соответственно через силу тока I и расстояния r1и г2 от проводов до точки А:
 ;
; 
Подставляя выражения B1и B2в формулу (1) и вынося  за знак корня, получаем
за знак корня, получаем

Вычислим cos α. Заметив, что 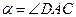 (как углы c соответственно перпендикулярными сторонами), по теореме косинусов запишем
(как углы c соответственно перпендикулярными сторонами), по теореме косинусов запишем

где d — расстояние между проводами. Отсюда

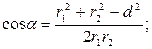
 .
.
Подставим в формулу (2) числовые значения физических величин и произведем вычисления:

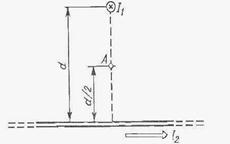
Пример 26. Длинный провод с током I= 50 А изогнут под углом  . Определить магнитную индукцию В в точке А (рис. 12). Расстояние d = 5 см.
. Определить магнитную индукцию В в точке А (рис. 12). Расстояние d = 5 см.
Решение. Изогнутый провод можно рассматривать как два длинных провода, концы которых соединены в точке О (рис. 13). В соответствии с принципом суперпозиции магнитных полей магнитная индукция В в точке А будет равна геометрической сумме магнитных индукции В1 и В2 полей, создаваемых отрезками длинных проводов 1 и 2, т. е. В=В1 + В2. Магнитная индукция В 2 равна нулю. Это следует из закона Био — Савара — Лапласа, согласно которому в точках, лежащих на оси привода,
 ([dlr])=0.
([dlr])=0.
Магнитную индукцию B1 найдем, воспользовавшись соотношением
 ,
,
где r0 — кратчайшее расстояние от провода 1до точки А (рис. 13).
 В нашем случае
В нашем случае 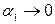 (провод длинный),
(провод длинный),  (cosα2=cos(2π/3)=-1/2). Расстояние
(cosα2=cos(2π/3)=-1/2). Расстояние  Тогда магнитная индукция
Тогда магнитная индукция
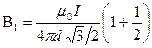
Так как B = B1(B2=0), то

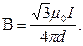
Вектор В сонаправлен с вектором В1 и определяется правилом правого винта. На рис. 13 это направление отмечено крестиком в кружочке (перпендикулярно плоскости чертежа, от нас).
Произведем вычисления:
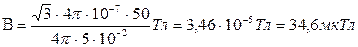
 Пример 27. Два бесконечно длинных провода скрещены под прямым углом (рис. 14). По проводам текут токи I1 = 80 А и I2=60 А. Расстояние d, между проводами равно 10 см. Определить магнитную индукцию В в точке A, одинаково удаленной от обоих проводов.
Пример 27. Два бесконечно длинных провода скрещены под прямым углом (рис. 14). По проводам текут токи I1 = 80 А и I2=60 А. Расстояние d, между проводами равно 10 см. Определить магнитную индукцию В в точке A, одинаково удаленной от обоих проводов.
 Решение. В соответствии с принципом суперпозиции магнитных полей магнитная индукция В поля, создаваемого токами I1и I2, определяется выражением
Решение. В соответствии с принципом суперпозиции магнитных полей магнитная индукция В поля, создаваемого токами I1и I2, определяется выражением
В = В1 + В2, где В1 — магнитная индукция поля, созданного в точке А током I1 ;В2 — магнитная индукция по-, созданного в точке Атоком I2.
Заметим, что векторы B1 и В2 взаимно перпендикулярны (их направления находятся по правилу буравчика и изображены в двух проекциях на рис. 15). Тогда модуль вектора В можно определить по теореме Пифагора:
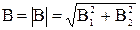 ,
,
где B1и В2 определяются по формулам расчета магнитной индукции для бесконечно длинного прямолинейного провода с током:


 и
и 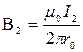
В нашем случае r0 = d/2. Тогда

Произведем вычисления:
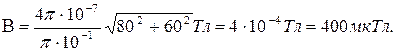
Пример 28. Бесконечно длинный провод изогнут так, как это изображено на рис. 16. Радиус R дуги окружности равен 10см. Определить магнитную индукцию В поля, создаваемого в точке О током I=80 А, текущим по этому проводу.
Решение. Магнитную индукцию В в точке О найдем, используя принцип суперпозиции магнитных полей: 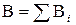 . В нашем случае провод можно разбить на три части (рис. 17): два прямолинейных провода (1 и 3), одним концом уходящие в бесконечность, и дугу полуокружности (2)радиуса R. Тогда
. В нашем случае провод можно разбить на три части (рис. 17): два прямолинейных провода (1 и 3), одним концом уходящие в бесконечность, и дугу полуокружности (2)радиуса R. Тогда
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 554; Нарушение авторских прав?; Мы поможем в написании вашей работы!