Становление олигополии 2 страница

Равновесие Бертрана ≈ Нэша представлено точкой В ≈ N на рис. 11. 7. Обратите внимание на то, что обе кривые реагирования Бертрана в отличие от кривых реагирования Курно (рис. 11. 3) восходящие. Это значит, что цены дуополистов Бертрана имеют выраженную тенденцию к сближению в противоположность выпускам дуополистов Курно.

Равновесие Бертрана достигается, если предположения дуополистов о ценовом поведении друг друга сбываются. Если дуополист 1 полагает, что его соперник установит цену P12 (рис. 11. 7), он в целях максимизации прибыли выберет, согласно своей кривой реагирования, цену P11. Но в таком случае дуополист 2 может на самом деле установить на свою продукцию цену P22, исходя из своей кривой реагирования. Если предположить (как мы это делали при рассмотрении равновесия Курно), что кривая реагирования дуополиста 1 круче, чем соответствующая кривая дуополиста 2, то тогда этот итеративный процесс приведет дуополистов к равновесию Бертрана ≈ Нэша (т. е. в точку В ≈ N на рис. 11. 7), где их кривые реагирования пересекутся. Маршрут их конвергенции в точку В≈N окажется подобен маршруту конвергенции выпусков дуополистов Курно, показанному стрелками на рис. 11. 4. Поскольку продукция обоих дуополистов однородна, каждый из них предпочтет в состоянии равновесия один и тот же уровень ее цены. В противном случае дуополист, назначивший более низкую цену, захватит весь рынок. Поэтому равновесие Бертрана≈Нэша характеризуется единой ценой, принадлежащей в двухмерном пространстве цен лучу, исходящему из начала координат под углом 45 градусов.

Кроме того, в состоянии равновесия Бертрана≈Нэша равновесная цена окажется равной предельным затратам каждого из дуополистов. В противном случае дуополисты, руководствуясь каждый стремлением овладеть всем рынком, будут снижать свои цены, а это их стремление может быть парализовано, лишь когда они уравняют свои цены не только между собой, но и с предельными затратами. Естественно, что в этом случае общая отраслевая прибыль окажется нулевой. Таким образом, несмотря на исключительную немногочисленность продавцов (в дуополии их лишь двое), модель Бертрана предсказывает, по сути дела, совершенно конкурентное равновесие отрасли, имеющей строение дуополии. 10

Пусть, как и в модели Курно (11. 6), рыночный спрос представлен линейной функцией Р = а - bQ, где Q = q1 + q2. Тогда обратная функция спроса будет

Q = q1 + q2 = (a/b) √ (1/b)P(11. 53)

Если при данной цене дуополиста 1, P1 > МС, дуополист 2 устанавливает цену З2 > МС, остаточный спрос дуополиста 1 будет зависеть от соотношения цен P1 и P2. А именно при P1 > P2, q1 = 0 все покупатели, привлеченные более низкой ценой, перейдут к дуополисту 2. Напротив, при P1 < P2 весь рыночный спрос окажется захваченным дуополистом 1. Наконец, в случае равенства цен обоих дуополистов, P1 = P2, рыночный спрос окажется поделенным между ними поровну и составит (а/b - 1/b P)0,5 для каждого.

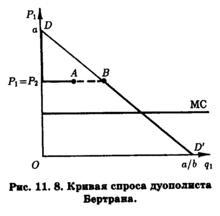
На рис. 11. 8 функция спроса дуополиста 1 отображена имеющей разрыв (АВ) кривой спроса DP2ABD'. Если дуополист 2 установит цену P2, то спрос на продукцию дуополиста 1 окажется нулевым, что соответствует вертикальному сегменту (DP2) его кривой спроса. При P1 = P2 рынок будет поделен поровну (сегмент P2А будет принадлежать дуополисту 1, а сегмент АВ дуополисту 2). Наконец, если дуополист 1 ответит на P2 снижением своей цены ниже этого уровня, он захватит весь рынок (сегмент BD'). Из рис. 11. 8 также видно, что каждое из предприятий-дуополистов может оставаться рентабельным, понемногу снижая цену с целью увеличения своей доли рыночного спроса до тех пор, пока не будет достигнуто равенство

P1 = P2 = MC,(11. 54)

которое и характеризует состояние равновесия Бертрана≈ Нэша.

Таким образом, в отличие от модели Курно, предсказывающей достижение совершенно конкурентного результата лишь по мере увеличения числа олигополистов, а именно когда п/(п + 1) приближается к единице, модель Бертрана предрекает совершенно конкурентный результат сразу же при переходе от монополии одного продавца к дуополии. Причина этого кардинального различия выводов в том, что каждый дуополист Курно сталкивается с нисходящей остаточной кривой спроса, тогда как дуополист Бертрана ≈ с кривой спроса совершенно эластичной по цене соперника, так что снижение цены оказывается прибыльным, пока она остается выше предельных затрат.

2.5. Модель Эджуорта

Согласившись с критикой модели Курно Бертраном, Ф. Эджуорт предложил модель ценовой дуополии с ограничением на величину производственной мощности дуополис-тов. На рис. 11. 9 это ограничение представлено абсциссой вертикально восходящего сегмента кривой МС (затраты на производство дополнительной ≈ сверх ограниченного масштаба мощности ≈ единицы продукции бесконечно велики) qk. Как видно из рис. 11. 9, мощности каждого дуопо-листа ограничены половиной рыночного спроса при цене, равной предельным затратам, qk = Q(P º MC)/2. Поэтому, если каждый из них установит начальную цену равной предельным затратам (P1 = P2 = МС), их совместный выпуск как раз и покроет совокупный рыночный спрос, Q(P = МС).

Если теперь дуополист 1 несколько повысит свою цену, тогда как дуополист 2 сохранит цену P2 = МС, все покупатели захотят перейти к нему вследствие более низкой цены. Однако ≈ и в этом отличие модели Эджуорта от модели Бертрана ≈ он Не сможет покрыть более половины рыночного спроса, поскольку именно такова его производственная мощность. Разочарованные неспособностью дуополиста 2 удовлетворить их спрос по относительно более низким ценам покупатели вынуждены будут обратиться к дуополисту 1. Столкнувшись с остаточным спросом (Q(P º МС) - qk), последний сможет максимизировать свою прибыль, действуя как монополист в отношении этого остаточного спроса. Его предельные затраты уравниваются с предельной выручкой в точке А, что предполагает установлением им прибылемаксимизирующей цены PJ, при которой выпуск составит q1 - Q(P = MC)/4.

В ответ на это дуополист 2 повысит свою цену до уровня чуть ниже P1, цены дуополиста 1, с тем чтобы привлечь к себе его покупателей. Однако из-за ограниченности своей производственной мощности дуополист 2 сможет покрыть спрос лишь в объеме Q1 - q1 = 2/3Q1 = Q1(P = МС)/2. Продавая по чуть более низкой, чем у дуополиста 1, цене вдвое больше продукции, дуополист 2 получит, вероятно, и вдвое большую прибыль. Тогда дуополист 1 в свою очередь снизит цену до уровня чуть ниже, чем цена дуополиста 2. Словом, они попытаются опередить друг друга в снижении цен. Попытки заработать на снижении цены будут продолжаться, пока она не достигнет уровня

P = MC + (P1 - MC)(q1/qk).

Дуополисты будут рассуждать примерно так. Если я снижу свою цену до Р, что чуть ниже цены соперника, я смогу продать максимально возможный для меня объем выпуска, qk. С другой стороны, если я увеличу свою цену до P1, я смогу продать лишь q1 единиц продукции. При какой цене Р моя прибыль окажется точно такой же, как и при цене P1? Ответ на этот вопрос можно получить, решив относительно Р уравнение

(P1 - MC)qi = (P - MC)q.

Но как только цена действительно упадет до Р, выгодным для любого дуополиста вновь становится повышение цены до P1, и весь ценовой цикл повторится. Таким образом, модель Эджуорта не предрекает никакого статичного равновесия. Скорее это некая "ценовая ловушка", попав в которую дуополисты втягиваются в нескончаемую ценовую войну, в которой падения цен чередуются с их всплесками.

2.6. Модель Стэкельберга

Модель Стэкельберга - модель дуополии, в которой учитывается возможная вероятная реакция конкурентов на принимаемые решения об объеме выпуска, причем одна или обе фирмы считают, что конкурент будет вести себя как дуополист Курно

Если, напр., фирма А предполагает, что конкурент будет реагировать соответственно кривой реакции Курно, то результаты для обеих фирм будут зависеть от поведения фирмы В. Тогда А получит большую прибыль, а В - меньшую, чем они получили бы при равновесии Курно. Но если и фирма В будет действовать согласно кривой реакции Стэкельберга, т. е. если каждая фирма неправильно предположит, что ее конкурент использует допущение Курно, то получаем равновесие Стэкельберга. В этом случае обе фирмы получат меньшую прибыль, чем при равновесии Курно.

В данной модели допускается ненулевая предположительная вариация. Пусть первая фирма предполагает, что вторая фирма будет реагировать соответственно кривой реакции Курно.

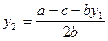
Исходя из этого, вычислим предположительную вариацию:

итак, у₁ и у₂ - равновесие Стэкельберга для фирмы №1.

Договорное решение.

В данной модели фирмы договариваются с целью максимизации прибыли.

П=П₁+П₂

П=a-by-by-c=0

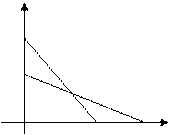y1

y2

Равновесие Стэкельберга

2.7. Тайный сговор и картели

В связи с тем, что во многих странах действует антимонопольное (антитрестовское) законодательство, открытое картелирование, базирующееся на письменных соглашениях, становится невозможным. В таких случаях соглашения заключаются неординарно и устно на конфиденциальных встречах. При этом используются изощренные формы камуфляжа согласованных действий олигополистов. В результате у потребителей, наблюдателей и контролирующих органов создается иллюзия ценовой конкуренции между олигополистами.

Наиболее изощренной формой тайных сговоров являются так называются джентльменские соглашения, которые заключаются в устной форме в непринужденной обстановке за рамками рабочего времени и которые весьма трудно выявляются с целью предъявления иска. Конечно, тайные соглашения о ценах требуют от их участников взаимного доверия и готовности пойти на компромиссы и уступки, чтобы добиться сбалансированности интересов участников. Расхождения в издержках, различия в целевых установках обуславливают далеко не одинаковое рыночное поведение олигополистов. В рамках тайных соглашений, которые фактически блокируют ценовую конкуренцию, могут развиваться неценовые формы конкуренции, сопровождаемые предоставлением скрытых скидок и дополнительных услуг, улучшением форм обслуживания клиентов, обеспечением наилучшим послесбытовым обслуживанием.

Картель представляет собой соглашение нескольких предприятий, устанавливающее для всех участников объем производства, цены на товар, условия найма рабочей силы, обмена патентами, разграничения рынков сбыта и долю каждого участника в общем, объеме производства и сбыта. Его целью является повышение цен (сверх конкурентного уровня), но не ограничение производственной и снабженческо-сбытовой деятельности участников.

На первый взгляд, сходство картеля с монополией очевидно. Но картель весьма редко, в отличие от монополии, контролирует весь рынок, ибо вынужден учитывать политику некартелизованных предприятий. Кроме того, участники картеля имеют довольно мощный соблазн обмануть своих партнеров, снижая цены или активно рекламируя свой товар, что создает условия для захвата части рынка. Вследствие этого многие картели представляют собой временную структуру рынка и встречаются редко. К тому же законодательство многих стран считает картельную практику незаконной и противодействует ей различными методами.

Невозможность полностью и постоянно использовать картель для взаимодействия олигополистических фирм вынуждает их идти на негласные экономические соглашения, тайную экономическую политику в области изменения цен и разграничения сфер влияния. Такое сотрудничество может проявляться как через особую экономическую политику олигополистических фирм в виде “жесткости цен” или “лидерства в ценообразовании”, так и через особые организации типа “патентных пулов” (или консорциумов).

Однако, в силу перечисленных выше причин, чаще всего развиты такие формы олигополии, при которых между фирмами отсутствует формальное соглашение о контроле над рынком.

Олигополия, значительно отличается от монополии. Суть ее в сплаве координации и конкуренции. В то же время действует и общее правило: чем меньше фирм в отрасли и чем крупнее каждая из них, тем легче им координировать свои действия и добиваться максимально высоких прибылей, регулируя цены на выпускаемую продукцию. И в этом смысле мы можем говорить о потенциальной опасности монополизации тех или иных отраслей экономики.

Кроме того, чем меньше фирм, тем менее эластичен по цене спрос потребителя на данном рынке. Вследствие этого фирма может повышать цены на свою продукцию, не неся больших потерь в объеме продаж.

3. Теория игр

Теория игр – наука, исследующая математическими методами поведение участников в вероятных ситуациях, связанных с принятием решений. Предметом этой теории являются игровые ситуации с заранее установленными правилами. В ходе игры возможны различные совместные действия – коалиции игроков, конфликты…

Часто отмечают, что в действительности олигополия - это игра характеров - игра, в которой так же, как в шахматах или в покере, каждый игрок должен предугадать действия соперника - его блеф, контрдействия, контрблеф - настолько, насколько это возможно. Поэтому экономисты, занимающиеся теорией олигополии, были восхищены появлением в 1944 году объемистой и высоко математезированной книги под названием “Теории игр и экономическое поведение”.

Стратегия игроков определяется целевой функцией, которая показывает выигрыш или проигрыш участника. Формы этих игр многообразны. Наиболее простая разновидность – игра с двумя участниками. Если в игре участвуют не менее трёх игроков, возможно образование коалиций, что усложняет анализ. С точки зрения платёжной суммы игры делятся на две группы – с нулевой и ненулевой суммами. Игры с нулевой суммой называют так же антагонистическими: выигрыш одних в точности равен проигрышу других, а общая сумма выигрыша равна 0. По характеру предварительной договорённости игры делятся на кооперативные и некооперативные.

Наиболее известный пример некооперативной игры с ненулевой суммой – “дилемма заключённого”.

Итак. С поличным поймали 2х воров, которым предъявлено обвинение в ряде краж. Перед каждым из них встаёт дилемма – признаваться ли в старых (недоказанных) кражах или нет. Если признается только 1 из воров, то признавшийся получает минимальный срок заключения – 1 год, а другой максимальный – 10 лет. Если оба вора одновременно сознаются, то оба получать небольшое снисхождение – 6 лет, если же оба не признаются, то понесут наказание, только за последнюю кражу – 3 года. Заключённые сидят в разных камерах и не могут договориться друг с другом. Перед нам игра с некооперативная с ненулевой (отрицательной) суммой. Характерной чертой этой игры является невыгодность для обоих участников руководствоваться своими частными интересами. “дилемма заключённого” наглядно показывает особенности олигополистического ценообразования.

3.1. Равновесие Нэша

(Названное в честь Джона Форбса Нэша) в теории игр - тип решений игры двух и более игроков, в котором ни один участник не может увеличить выигрыш, изменив своё решение в одностороннем порядке, когда другие участники не меняют решения. Такая совокупность стратегий выбранных участниками и их выигрыши называются равновесием Нэша.

Концепция равновесия Нэша (РН) не совсем точно придумана Нэшем, Антуан Августин Курно показал, как найти то, что мы называем равновесием Нэша в игре Курно. Соответственно, некоторые авторы называют его равновесием Нэша-Курно. Однако Нэш первым показал в своей диссертации Некооперативные игры (1950), что равновесия Нэша должны существовать для всех конечных игр с любым числом игроков. До Нэша это было доказано только для игр с 2 участниками с нулевой суммой Джоном фон Нейманом и Оскаром Моргернштерном (1947).

Формальное определение.

Допустим, 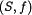- игра n лиц в нормальной форме, где 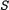- набор чистых стратегий, а - набор выигрышей. Когда каждый игрок выбирает стратегию в профиле стратегий игрок получает выигрыш . метьте, что выигрыш зависит от всего профиля стратегий: не только от стратегии, выбранной самим игроком , но и от чужих стратегий. Профиль стратегий 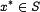является равновесием по Нэшу, если изменение своей стратегии не выгодно ни одному игроку, то есть для любого :

Игра может иметь равновесие Нэша в чистых стратегиях или в смешанных (то есть при выборе чистой стратегии стохастически с фиксированной частотой). Нэш доказал, что если разрешить смешанные стратегии, тогда в каждой игре n игроков будет хотя бы одно равновесие Нэша.

4. Формирование цен на олигополистическом рынке

Обобщая существенные свойства вышеприведенных моделей, предположим, что каждая фирма считает цены и объем выпуска конкурентов зафиксированными и максимизирует прибыль вдоль своей кривой реакции. В этом случае между предположением и действительным поведе-нием возникает несовместимость. Она может быть весьма критической, так как не существует возможности “компенсации”, если принятое управленческое решение оказалось неудовлетворительным.

В многопериодной модели фирмы обладают возможностью изучить своих конкурентов и использовать опыт их поведения в качестве основы для определения конкретных последствий любой инициативы. Существует также возможность исправить положение, если в предшествующем периоде фирма приняла неудовлетворительное управленческое решение и соответственно пострадала.

Ценовое приспособление фирм - олигополистов друг к другу начнется со снижения цен, но затем они перейдут к повышению цен и совместной максимизации прибыли.

Однако это справедливо только при отсутствии на рынке тайного картельного соглашения, которое предполагало бы согласованность действий предприятий-конкурентов по установлению цен и объемов выпуска.

Рассмотрим процесс олигополистического ценообразования, происходящий в реальной действительности. В своей наиболее общей форме он зависит от трех основных эле-ментов: условий спроса, функции издержек фирмы и предположения о максимизации прибыли для каждого предприятия. Особо следует учитывать, что это происходит в условиях полной определенности, т. е. предполагается, что участники рынка знают все о его текущем состоянии.

В условиях олигополистического равновесия Курно доля рынка фирмы находится в обратной зависимости от уровня ее средних издержек. Поэтому, если со стороны спросовых ограничений абсолютное значение эластичности спроса растет, то рентабельность фирмы падает, и если издержки производства единицы продукции постоянны, то и цена товара будет постоянной.

В ходе исследования процесса установления цены и объемов выпуска в условиях олигополии делалось предположение, что фирмы действуют в условиях определенности. Однако на практике, даже если фирмы обладают полной информацией о собственной структуре издержек, они очень редко знают условия спроса, с которыми им предстоит столкнуться.

Решение данной проблемы возможно по двум направлениям. Первое направление продолжает концентрироваться на ценовом поведении продавцов продукта, но вводит фактор неопределенности в кривую спроса рынка. Данная позиция основывается на трех основных идеях. Во-первых, это так называемый “принцип увеличивающейся неопре-деленности”, предполагающий, что дисперсия общего возможного дохода, получаемого в результате принятия решения продавцом по ценам или объему выпуска, будет увели-чиваться так же, как и ожидаемая сумма дохода. Во-вторых, предполагается, что люди, принимающие решения, не приемлют риска, т. е. им необходимо намного большее увеличение ожидаемой прибыли для компенсации постоянно возрастающего риска, измеряемого дисперсией прибыли. В-третьих, в отличие от случая определенности, необходимо установить различие между фирмами, которые устанавливают цену и продают запрашиваемое количество товара, и теми фирмами, которые устанавливают определенный объем выпуска и продают его по любой сложившейся цене. Это связано с тем, что в последнем случае неизвестен размер общего дохода, хотя известны общие издержки предприятия, а в первом случае и то и другое неизвестно. Из вышеизложенного следует, что фирме, устанавливающей объем выпуска, легче использовать экономический анализ при планировании.

Введение фактора неопределенности в модель поднимает и другую проблему. Неопределенность означает, что раз-личные фирмы могут устанавливать различные цены на однородные товары (политика дискриминации); следовательно, необходимо обратить внимание на поведение потребителей. Изучение обеих сторон рынка одновременно - это и есть второе основное направление анализа решений предприятий по ценам и объему выпуска в условиях неопределенности. При большем разбросе цен однородных товаров рациональным для потребителя продукта будет поиск наименьшей цены, но только до тех пор, пока ожидаемый доход от этого поиска не перекроется затратами на сам поиск. Однако часть исследователей указывают на то, что если фирмы, функционирующие на олигополистическом рынке, максимизируют прибыль, то все они установят одну и ту же цену, и дисперсия цен исчезнет, т. е. товары станут полностью гомогенными.

Одновременно, если потребители и поставщики не обладают информацией о распределении цен, то предположение об установлении единственной цены становится лож-ным. Ценовая дисперсия может существовать, если разные потребители обладают разным уровнем затрат на поиск необходимого товара.

Основная проблема введения фактора неполной (асимметричной) информации в модель олигополистического рынка заключается в наличии большого числа возможных результатов, зависящих от предположений о природе информации. Для этого необходимо знать, что общеизвестно на рынке, а что известно лишь некоторым фирмам, какова асимметрия в распределении информации, до какой степени фирмы нуждаются в информации и как в течение времени развертывается процесс уравновешивания

4.1. Ценовая конкуренция и ценовые “войны”

В условиях ограниченного числа поставщиков определенного товара их поведение можно описать двояким образом. Повышение или понижение цены на товар одним из товаропроизводителей вызывает адекватную реакцию конкурентов. В данном случае действия конкурентов нейтрализуют преимущество в цене, которого пытался добиться один из хозяйственных субъектов. В результате между конкурентами фактически не происходит перераспределение общих объёмов продаж, каждый из конкурентов не ощущает потери своих покупателей. Если и происходит отток или приток покупателей, то это ощущает отрасль в целом под воздействием понижения или повышения цен всеми товаропроизводителями. В зависимости от направления динамики цен покупатели будут искать способы удовлетворения своих потребностей путем расширения объема закупок товаров в данной отрасли или в других отраслях.

В реальной действительности в зависимости от конкретно складывающихся обстоятельств поведение конкурентов в качестве ответной реакции на действия одного из олигополистов может быть весьма разнообразным. Однако наиболее достоверной реакцией можно считать то, что понижение цены кем-либо из конкурентов вызовет стремление у остальных выровнять свои цены, т. е. понизить их с целью не допустить расширения рынка продаж конкурента-инициатора. В то же время повышения цен одним из товаропроизводителей, как правило, оставляют без внимания. Такое игнорирование повышения цен со стороны конкурентов связано с надеждой увеличить свои доли в общем объеме продаж за счет того из олигополистов, который рискнул поднять цену на свой продукт. Для наглядности обратимся к рисунку 6, на котором показаны кривые спроса олигополиста.

Рисунок 6. Ломаная кривая спроса олигополиста

Если представить, что кривая спроса выражает положение олигополиста в условиях, когда его конкуренты выравнивают свои цены по его ценам, а кривая спроса соответствует игнорированию конкурентами изменения цен этим олигополистом, то можно сделать вывод о наличии кривой спроса 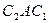у олигополиста в условиях ценовой конкуренции. Такого рода заключение вытекает из неоднозначной реакции конкурентов на повышение или понижение цен одним из олигополистов. В случае установления цены и объема выпуска, соответствующих точке А, положение предприятия характеризуется равновесным состоянием. Однако если предприятие примет решение о повышении цены на свою продукцию, а его конкуренты на это никак не отреагируют, то положение на рынке предприятия-инициатора будет характеризоваться отрезком кривой спроса . В результате того, что на данном отрезке спрос обладает относительно высокой эластичностью, повышение цены приведет к сокращению объема продаж предприятием, тогда как его конкуренты получат дополнительных покупателей.

Но если предприятие предпримет попытку понизить цену, то остальные олигополисты моментально отреагируют соответствующим понижением цен на свою продукцию. В этом случае состояние спроса будет характеризоваться отрезком . Этой части кривой спроса присуща более низкая эластичность, следовательно, понижение цены не позволит заметно увеличить объемы продаж.

При этом необходимо заметить, что и кривая предельного дохода имеет необычную форму: она состоит также из двух отрезков. Первый отрезок кривой предельного дохода соответствует кривой спроса , второй – . Наличие переломного момента в эластичности спроса в точке А обуславливает разрыв кривой предельного дохода, т. е. появляется вертикальный отрезок BE кривой предельного дохода . Данный разрыв в кривой предельного дохода наводит на мысль о том, что фактически любые изменения в предельных издержках в границах между кривыми предельных издержек 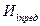и 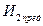не будут оказывать влияние на цену и объем производства, так как точка пересечения вертикального отрезка кривой предельного дохода (ВЕ) с кривой предельных издержек будет указывать на неизменность масштаба производства (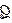), максимизирующего прибыль.

Сдержанный характер ценовой конкуренции связан, во-первых, со слабыми надеждами на достижение рыночных преимуществ по сравнению с конкурентами, а во-вторых, с риском развязывания “войны” цен.

Ценовая война - цикл последовательных уменьшений цены соперничающими на олигополистическом рынке фирмами. Она является одним из многих возможных последствий олигополистического соперничества. Войны цен хороши для потребителей, но плохи для прибылей продавцов.

Легко понять, как фирмы втягиваются в эту войну. Поскольку каждый продавец думает, что другой не будет реагировать на его понижение цены, то у каждого из них есть искушение увеличить продажи, сокращая цены. Снижая цену ниже цены своего конкурента, каждый продавец может захватить весь рынок - или он так думает - и может тем самым увеличить прибыль. Но конкурент отвечает понижением цены. Война цен продолжается до тех пор, пока цена не падает до уровня средних издержек. В равновесии оба продавца назначают одну и ту же цену P=AC=MC. Общий рыночный выпуск такой же, какой имел бы место при совершенной конкуренции. Предполагая, что каждая фирма всегда поддерживает свою текущую цену, другая фирма всегда может увеличить прибыль, требуя на 1 рубль меньше, чем ее соперница. Конечно, другая фирма не сохранит прежнюю цену, т. к. она осознает, что может получить большую прибыль, требуя на 1 копейку меньше конкурента.

Дата добавления: 2014-11-16