
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Система сходящихся сил на плоскости и в пространстве
|
|
|
|
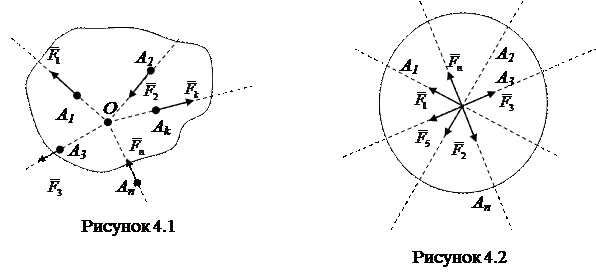 Система сил, линии, действия которых пересекаются одной точке, называется системой сходящихся сил (рисунок 4.1).
Система сил, линии, действия которых пересекаются одной точке, называется системой сходящихся сил (рисунок 4.1).

 | |||||||||||
 | |||||||||||
 | |||||||||||
 | |||||||||||
 |  |
Так как силы можно переносить по линии их действия, то эту систему сил всегда можно заменить системой сил, приложенных к одной точке (рисунок 4.2).
Рассмотрим два способа сложения сходящихся сил: графический и аналитический.
4.1 Графический способ сложения сил
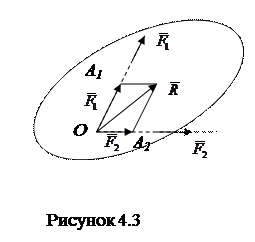
Равнодействующая двух сил, приложенных к одной точке, находится согласно аксиоме параллелограмма сил как диагональ параллелограмма, построенного на этих силах (рисунок 4.3), или как замыкающая сторона силового треугольника (рисунок 4.4). Следовательно, равнодействующая двух сил равна их геометрической сумме:
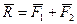 (4.1)
(4.1)
|
|
|
|
|



Найдем равнодействующую системы сходящихся сил  . Будем складывать их последовательно по правилу силового треугольника (Рисунок 4.5).
. Будем складывать их последовательно по правилу силового треугольника (Рисунок 4.5).
Чтобы найти равнодействующую системы сходящихся сил графическим способом, надо построить в точке пересечения их действия силовой многоугольник на слагаемых силах, т.е. к концу вектора первой силы приложить вектор, геометрически равный второй силе и т.д.
Вектор, соединяющий начало первого слагаемого вектора с концом последнего, т.е. замыкающая сторона силового многоугольника, является равнодействующей системы сходящихся сил.
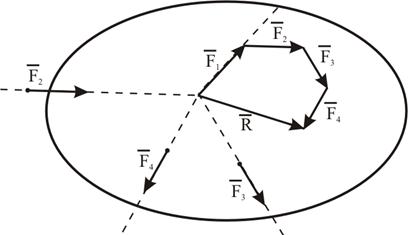
Рисунок 4.5
 (4.2)
(4.2)
Величину 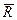 , равную геометрической сумме сил какой-нибудь системы, будем в дальнейшем называть главным вектором этой системы.
, равную геометрической сумме сил какой-нибудь системы, будем в дальнейшем называть главным вектором этой системы.
4.2 Аналитический способ сложения сходящихся сил
Чтобы сложить сходящиеся силы аналитическим способом, надо вычислить проекции этих сил на оси прямоугольных координат.
 Найдем проекции сил на ось, когда силы и ось лежат в одной плоскости (Рисунок 4.6).
Найдем проекции сил на ось, когда силы и ось лежат в одной плоскости (Рисунок 4.6).
|
|
|
|

Проекция силы на ось (по величине и по знаку) равна произведению модуля силы на косинус угла между направлением силы и положительным направлением оси.
 (4.3)
(4.3)
Обозначим проекции сил  соответственно
соответственно 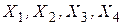 . Из рисунка видно, что эти проекции будут равны:
. Из рисунка видно, что эти проекции будут равны:
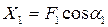 ;
; 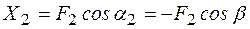 ;
;
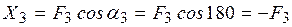 ;
; 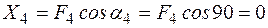 .
.
Теперь вычислим проекцию силы  на оси прямоугольных координат
на оси прямоугольных координат  в случае, когда сила произвольно расположена в пространстве (рисунок 4.7).
в случае, когда сила произвольно расположена в пространстве (рисунок 4.7).
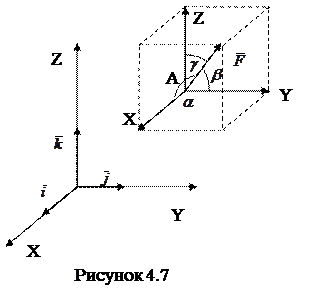

Разложим силу 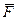 на составляющие вдоль осей координат:
на составляющие вдоль осей координат:
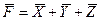 или
или 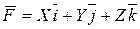 (4.4)
(4.4)
где 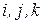 – орты прямоугольных осей координат;
– орты прямоугольных осей координат;
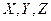 – проекции силы
– проекции силы 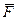 на соответствующие оси координат.
на соответствующие оси координат.
Проекции силы на оси прямоугольных координат определяются по формулам:
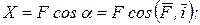
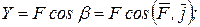
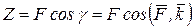 (4.5)
(4.5)
Если известны проекции силы на оси координат, то модуль силы определяется по формуле, как диагональ прямоугольного параллелепипеда:
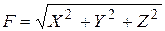 (4.6)
(4.6)
А ее направление по трем направляющим косинусам:
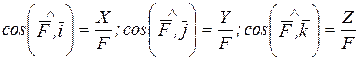 (4.7)
(4.7)
Найдем равнодействующую 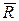 системы сходящихся сил аналитическим способом. Известно, что равнодействующая системы сходящихся сил определяется геометрически их геометрической суммой:
системы сходящихся сил аналитическим способом. Известно, что равнодействующая системы сходящихся сил определяется геометрически их геометрической суммой: 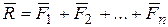 .
.
Спроектируем это векторное равенство на оси прямоугольной системы координат и найдем проекции равнодействующей 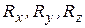 :
:
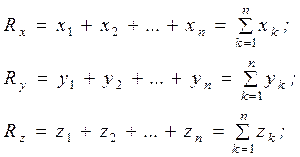 (4.8)
(4.8)
Модуль равнодействующей силы определится согласно формуле (3.6):
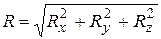 (4.9)
(4.9)
А направление по трем направляющим конусам:
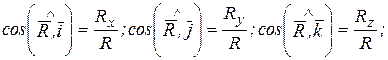 (4.10)
(4.10)
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 1853; Нарушение авторских прав?; Мы поможем в написании вашей работы!
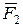
 1
1
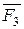 1
1
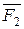 1
1
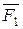 1
1