Пара сил

1. Какая система сил называется парой?

2. Почему пара сил не имеет равнодействующей?

3. Чем характеризуется действие пары сил на тело?

4. Как направлен вектор момента пары сил?

5. Как определяются моменты пар сил, лежащих в одной плоскости.

6. Каковы условия эквивалентности пар сил на плоскости и в пространстве?

7. Какие преобразования пары сил не изменяют ее действие на твердое тело?

8. Почему момент пары сил является свободным вектором?

9. Чему равен момент пары сил, эквивалентной двум парам сил, расположенным в перпендикулярных плоскостях, если M₁=10мм; М₂=20нм?

10. Чему равен момент пары сил, эквивалентной системе пар сил, расположенных в пространстве и в одной плоскости?

11. Каковы условия равновесия системы пар сил, расположенных в пространстве и в одной плоскости?

12. Чем можно уравновесить заданную пару сил?

6 Приведение системы сил к центру. Условия равновесия

6.1 Теорема о параллельном переносе силы

Равнодействующая системы сходящихся сил непосредственно находится с помощью закона параллелограмма сил. Очевидно, что аналогичную задачу можно будет решить и для произвольной системы сил, если найти для них метод, позволяющий перенести все силы в одну точку. Такой метод дает следующая теорема: силу, приложенную к абсолютно твердому телу, можно, не изменяя оказываемого ею действия, переносить из данной точки в любую другую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, куда сила переносится.

Этот метод был предложен французским ученым Пуансо (1777-1859 г.), и называется приведением силы к заданному центру. Пусть на твердое тело действует сила 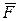, приложенная в точке A (рисунок 6.1 а))

Рисунок 6.1

Действие этой силы не изменяется, если в любой точке B тела приложить две уравновешенные силы 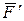и 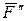, такие, что 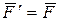; . Полученная система трех сил и представляет собой силу 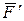, равную 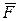, но приложенную в точке B, и пару 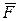, 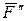с моментом

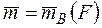(6.1)

Равенство (6.1) следует из формулы (5.7). Таким образом, теорема доказана. Результат, даваемый теоремой, можно еще изобразить так, как показано на рисунке 6.1 б), силу 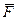на этом рисунке надо считать отброшенной. Точку B, куда переносится сила, часто называют точкой приведения.

Пусть на твердое тело действует произвольная система сил, (рисунок 6.2 а). Выберем произвольную точу O за центр приведения и, пользуясь доказанной выше теоремой, перенесем все силы в центр O, присоединяя при этом соответствующие пары (рисунок 6.2 б). Тогда на тело будет действовать система сил:

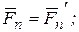… (6.2)

приложенных в центре O, и система пар, моменты которых согласно формуле (6.1), равны:

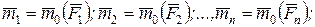(6.3)

(Силы переносятся параллельно самим себе и равными по модулю).

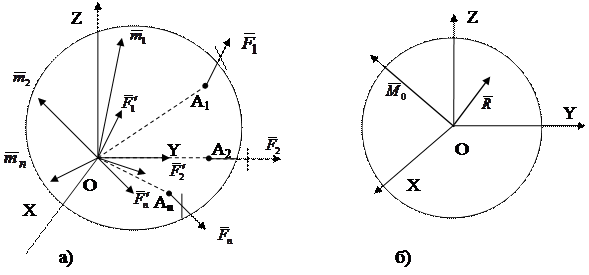
Рисунок 6.2

Сходящиеся в точке O силы заменяются одной силой 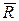, приложенной в точке O. При этом

(6.4)

Чтобы сложить все полученные пары, надо сложить векторы моментов этих пар. В результате система пар заменится одной парой, момент которой:

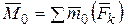(6.5)

т.е. .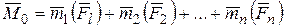

Величина 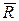, равная геометрической сумме всех сил, называется главным вектором системы сил; величина 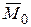, равная геометрической сумме моментов всех сил относительно центра O, называется главным моментом системы сил относительно этого центра.

Таким образом, любая система сил, действующих на абсолютно твердое тело, при приведении к произвольно выбранному центру O заменяется одной силой, 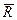, равной главному вектору системы сил и приложенной в центре приведения O, и одной парой с моментом 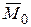, равным главному моменту системы сил относительно центра O (рисунок 6.2 б).

Следует отметить, что сила 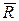не является равнодействующей даннойсистемы сил, так как заменяет систему сил не одна, а вместе с парой.

Из рассмотренного следует, что две системы сил, имеющие одинаковые главные векторы и главные моменты относительно одного и того же центра, эквивалентны (условие эквивалентности сил).

Отметим также, что значение 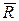от выбора центра O не зависит, а значение 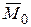при изменении положения центра O, может в общем случае изменяться вследствие изменения значений моментов отдельных сил. Поэтому всегда необходимо указывать, относительно какого центра определяется главный момент.

Рассмотрим в заключение два частных случая:

1) если для данной системы сил 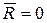; , то она приводится к одной паре сил с моментом 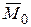. В этом случае значение 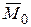не зависит от центра O, так как иначе получилось бы, что одна и та же система сил заменяется разными, но эквивалентными друг другу парами, что невозможно.

2) если для данной системы сил 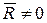, а 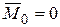, то она приводится к одной силе, т.е. равнодействующей, равной 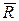и приложенной в центре O.

6.2 Условия равновесия системы сил. Теорема о моменте равнодействующей

(теорема Вариньона)

Покажем, что для равновесия любой системы сил необходимо и достаточно, чтобы главный вектор этой системы сил и ее главный момент относительно любого центра были равны нулю, т.е. чтобы выполнялись условия:

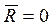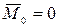, (6.6)

где O – любой центр.

Условия (6.6) являются необходимыми, так как если какое-нибудь из них не выполняется, то система действующих на тело сил приводится или к равнодействующей (когда 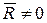), или к паре сил (когда ) и, следовательно, не является уравновешенной. Одновременно условия (6.6) являются и достаточными, потому что при 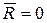система сил может приводиться только к паре с моментом 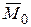, а так как 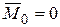, то имеет место равновесие.

Пользуясь полученным результатом, докажем теорему Вариньона о моменте равнодействующей: если данная система сил имеет равнодействующую, то момент равнодействующей относительно любого центра O равен сумме моментов сил системы относительно того же центра.

Пусть система сил приводится к равнодействующей 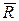, линия действия которой проходит через точку C (рисунок 6.3). Приложим к этой точке силу 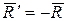. Тогда система сил , 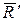будет находиться в равновесии, и для нее должно выполняться условие , т.е. согласно формуле (6.5) для данных сил, включая силу 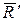, должно быть 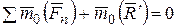. Но так как 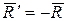, и обе силы направлены вдоль одной прямой, то 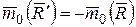, т.е. можно записать

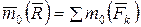(6.7)

Т.е. теорема доказана. Ею удобно пользоваться при вычислении моментов сил.

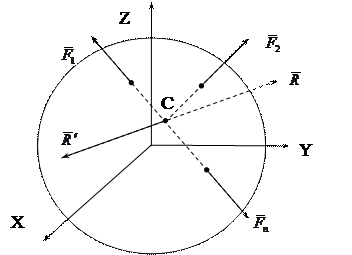
Рисунок 6.3

Вопросы для самоконтроля

1. Сформулируйте теорему о параллельном переносе силы.

2. Что называется главным вектором системы сил?

3. Что называется главным моментом системы сил?

4. Как геометрически определяется главный вектор системы сил?

5. Определите главный вектор системы сил, которая изображена на рисунке, если F₁ = 10 H, F₂ = 50 H, F₃ = 30 H, OA = 4 м, ОВ = 0,6 м, ОС = 0,3 м.

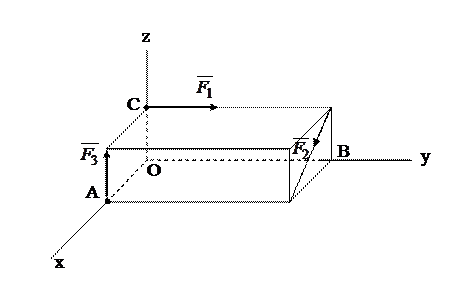
6. Запишите формулы, с помощью которых аналитически определяется главный момент системы сил относительно выбранной точки.

7. Определите главный момент системы сил, которая задана в задаче 5, относительно начала координат.

8. Зависят ли главный вектор и главный момент заданной системы сил от выбора центра приведения.

9. При каком условии сила, равная главному вектору плоской системы сил, является равнодействующей этой системы сил?

Дата добавления: 2014-11-08