Пространственные представленияи воображение

+ _|_--------+ _

- + - + - + -

+-----+--------

+ - + - + - +

Белоснежка и семь гномов. В торце стола сидит Белоснежка, справа

сидит Тото, затем Коко, затем Кото. Напротив Белоснежки сидит Кико, справа от Кико — Тато, затем Тико и, наконец, слева от Белоснежки — Кито.

Вот характеристика каждого гнома: Тико — пьет чай, любит пирог с маком, имеет одежду зеленого цвета, содержит попугая, на посуде имеет изображение лилии, носит сандалии, дежурит во вторник.

Коко — кофе с молоком, жареное мясо, белая одежда, собака, тюльпан, тапочки, понедельник.

Кото — вода, блины, синяя одежда, канарейка, фиалка, полуботинки, пятница.

Тато — черный кофе, голубцы, черная одежда, золотые рыбки, мак, лапти, среда.

Кико — молоко, холодец, коричневая одежда, ежик, незабудка, сапоги, суббота.

Кито — ситро, уха, желтая одежда, неоны, маргаритки, мокасины, воскресенье.

Тото — какао, гуляш, красная одежда, кошка, роза, ботинки, четверг.

Развертка куба (рис. 36).

Лабиринт «лента». На первой схеме рис. 37 показан один из способов прохождения лабиринта.

Второй способ приведен на другой схеме. По правой ветви проходим до петли (см. третью схему), делая при этом 3 переворота. Проходим петлю с четвертым переворотом, идем обратно по другой стороне и оказываемся с нижней невидимой стороны. Затем переходим на путь, указанный на второй схеме, и приходим в точку 0 с нижней стороны.

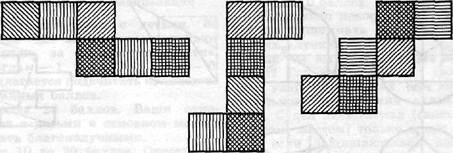
Рис. 36.

Квадраты и треугольники. Четыре спички можно переложить таким способом (рис. 38).

Урок географии (рис. 39). Разместить три флага довольно просто: один можно поставить на Южном полюсе, а два других — по обе стороны ст него, на 120° севернее, т. е. на 30-й параллели северной широты. Например, в западном полушарии флаг можно поставить блиа Нового Орлеана, при впадении р. Миссисипи в Мексиканский залив, а в восточном — где-то на Гималаях, несколько северо-восточнее Джомолунгмы (Эвереста).

Четыре равноудаленные точки на поверхности шара можно определить при помощи вписанного в него куба. Это будут точки 1, 2, 3 и 4 (см. рисунок). Применительно к глобусу первые две будут лежать на 35-й параллели северной широты, а две другие — на 35-й южной параллели со смещением относительно первых на 90° по долготе.

Соответственно этому первый флаг можно поставить на западном побережье Северной Америки, между Сан-Франциско и Лос-Анджелесом. Второй — на Ближнем Востоке, в районе границы Ирана и Афганистана. Третий — около Сиднея

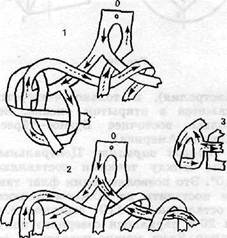
Рис. 37.

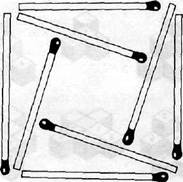
Рис. 38.

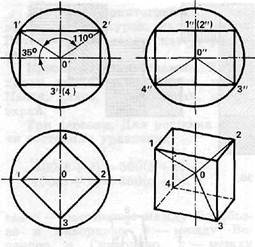
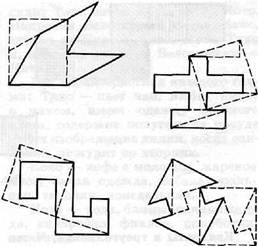
Рис. 39.

Рис. 40.

(Австралия), и только четвертый окажется в открытом океане, несколько восточнее Буэнос-Айреса (Южная Америка).

Второй вариант. Центральные углы между точками составляют 110°. Это позволяет один флаг также поставить на Южном полюсе, а остальные на 110° севернее, т.е. на 20-й параллели северного полушария. Здесь можно указать на такие пункты: для второго флага —

полуостров Юкатан (Мексика), для третьего — левое побережье р. Нил (Африка), а четвертый флаг тоже окажется в открытом океане, восточнее группы Марианских островов.

Квадрирование фигур (рис. 40).

Поворот с разворотом. Фигура № 7.

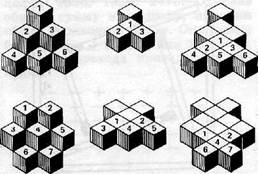
Сосчитайте кубики. Пределом видимости служат внешние очертания каждой группы. Все, что может поместиться в эти контуры, и будет ответом на поставленный вопрос.

На рисунке 41 показаны обе группы кубиков и отдельно их средние и нижние слои. Кубики пронумерованы, причем расположенные один под другим обозначены одной и той же цифрой.

Всего получилось: в первой группе 1+ 4 +10 = 15, во второй 2-f-13^23.

Рис. 41.

Дата добавления: 2014-11-16