Способы работы с векторными величинами

СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ВЕЛИЧИНЫ

МАТЕМАТИЧЕСКИЕ ОСНОВЫ ФИЗИКИ

СКАЛЯРНЫМИ величинами (скалярами) называются такие величины, которые характеризуются только числовым значением (пройденный путь l, время t, масса m, энергия Е, работа А, потенциал 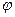и др.).

Математические действия со скалярами производятся алгебраически.

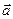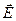ВЕКТОРНЫМИ величинами (векторами) называются такие величины, которые характеризуются числовым значением и направлением (скорость перемещение , ускорение , сила , напряженность и др.).

1. ГЕОМЕТРИЧЕСКОЕ СЛОЖЕНИЕ ВЕКТОРОВ.

а) Правило параллелограмма: вектора 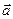и откладываются от одной точки, результирующий вектор 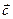совпадает с диагональю параллелограмма и начинается в той же точке, от которой откладывались вектора 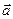и .

б) Правило треугольника: от конца вектора 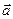откладывается вектор 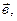начало результирующего вектора 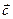совпадает с началом вектора 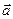, а конец совпадает с концом вектора .

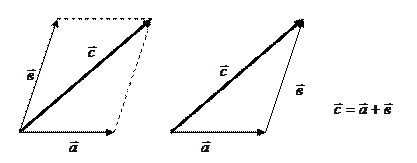
Для вычисления модуля результирующего вектора необходимо использовать законы геометрии (см. раздел «Соотношения в прямоугольном и произвольном треугольниках).

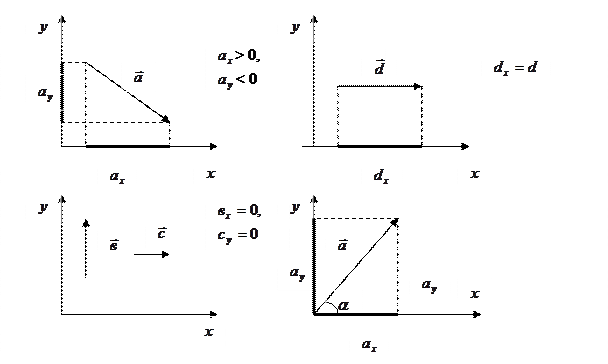
2. НАХОЖДЕНИЕ ПРОЕКЦИЙ ВЕКТОРОВ НА ОСИ КООРДИНАТ.

Чтобы найти проекцию вектора 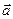на ось 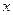, необходимо на эту ось опустить перпендикуляры из начала и конца вектора. Отрезок 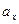на оси между этими перпендикулярами и будет проекцией вектора 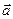на ось .

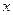Аналогично находятся проекции на другие оси.

Проекция вектора на ось - скалярная величина, поэтому математические действия с проекциями производятся алгебраически.

Если при перемещении от начала проекции к ее концу движутся по направлению оси, то проекция вектора на эту ось положительна, в противном случае отрицательна.

Если вектор перпендикулярен оси, то его проекция на эту ось равна нулю.

Если вектор параллелен оси, то модуль проекции равен длине вектора.

Если вектор 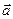составляет некоторый угол 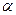с осью, то его проекция , .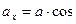

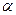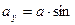
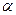Из рисунка видно, что 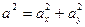(по теореме Пифагора).

Дата добавления: 2014-11-16