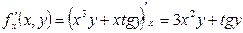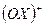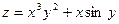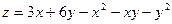КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные формулы. 1. - частная производная 1-го порядка функции z по переменной x
|
|
|
|
1. 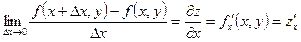 - частная производная 1-го порядка функции z по переменной x.
- частная производная 1-го порядка функции z по переменной x.
2.  - частная производная 1-го порядка функции Z по переменной y.
- частная производная 1-го порядка функции Z по переменной y.
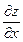 вычисляется при постоянном y,
вычисляется при постоянном y, 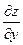 вычисляется при постоянном x.
вычисляется при постоянном x.
При вычислении 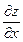 ,
, 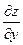 используются правила и формулы дифференцирования (смотреть таблицу производных).
используются правила и формулы дифференцирования (смотреть таблицу производных).
полный дифференциал функции 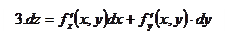
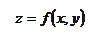
где 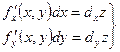 - частные дифференциалы
- частные дифференциалы
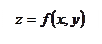 функции
функции
4.  Для дифференцируемой функции справедливы приближённые равенства.
Для дифференцируемой функции справедливы приближённые равенства.


а), где - полное приращение функции.
 , dz- полный дифференциал.
, dz- полный дифференциал.
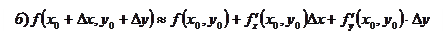
Эта функция используется в нахождении приближённых значений функции.
 5.Частными производными второго порядка от функции
5.Частными производными второго порядка от функции 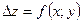 называются частные производные от её частных производных первого
называются частные производные от её частных производных первого
 порядка.
порядка.
6. 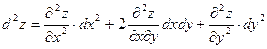 - дифференциал второго порядка для функции
- дифференциал второго порядка для функции 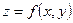
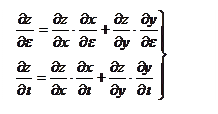
 7. Если z= f(x,y), где x= φ(t), y=ψ(t), то
7. Если z= f(x,y), где x= φ(t), y=ψ(t), то 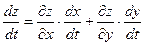 - производная сложной функции. z=f(φ(t),ψ(t)).
- производная сложной функции. z=f(φ(t),ψ(t)).
8. Если z=f(x,y), где 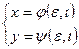 то
то
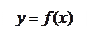
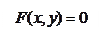 9. Производная неявной функции, заданной уравнением,где F(x,y)-дифференцируемая функция,
9. Производная неявной функции, заданной уравнением,где F(x,y)-дифференцируемая функция,
вычисляется по формуле:
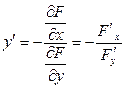

 10. Частные производные неявной функции заданной уравнением вычисляются по формулам:
10. Частные производные неявной функции заданной уравнением вычисляются по формулам:
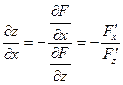
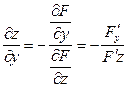 при условии
при условии 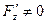
9.3 Примеры решения задач.
Задача 1.
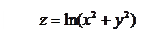
 Найти
Найти 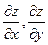 .
.
Решение:
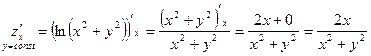
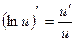 , где
, где 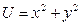
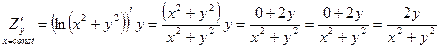
Задача 2. Найти полный дифференциал функции z= x3y+ xtgx
Решение: 
- теоретическая формула.
|
Где



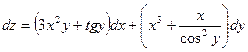
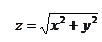
Задача 3. Вычислить приближённое значение функции в точке P(2,97;4,02)
Решение:
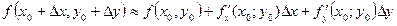
т.Р 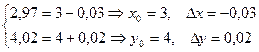
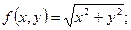
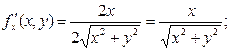
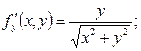
Тогда 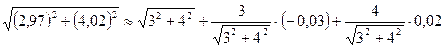
Или 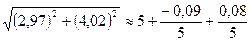
Или 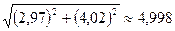
|
Задача 4. Найти производную функции в направлении, составляющим с положительным направлением оси (ОХ) угол a=60°.
Решение:
|
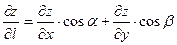 , где aи b- углы наклона вектора
, где aи b- углы наклона вектора 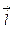 к оси и к оси (OY)+ соответственно.
к оси и к оси (OY)+ соответственно.
a=60°, тогда b=30° 
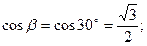
|
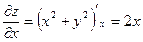
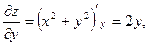
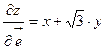 - ответ.
- ответ.
Задача 5. Вычислить градиент функции 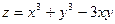 в точке А (2;1).
в точке А (2;1).
Решение:
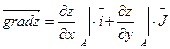 , где
, где 
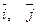 - базисные векторы, орты.
- базисные векторы, орты.
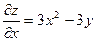
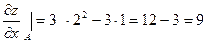
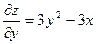
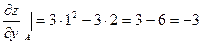
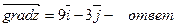
|
Задача 6. Найти смешанные частные производные второго порядка функции
Решение:
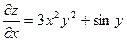
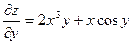
Дифференцируя, 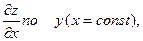 получаем
получаем 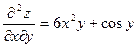
Дифференцируя 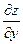 по x(y=const), получаем
по x(y=const), получаем 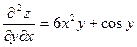
Ответ: 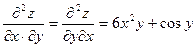
|
Задача 7. Исследовать на экстремум функцию
Решение: (1)  - необходимое условие экстремума.
- необходимое условие экстремума.
(2)  где
где 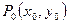 является решением системы (1).
является решением системы (1).
Неравенство (2) является достаточным условием экстремума.
Причём, если 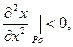 то в точке
то в точке 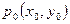 есть максимум функции.
есть максимум функции.
И если 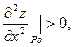 то в точке
то в точке 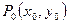 есть минимум функции.
есть минимум функции.
Имеем: 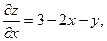
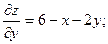
 (1)
(1) 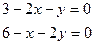 Þ
Þ 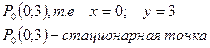
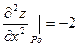
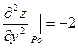
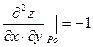
|
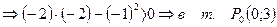
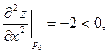
то в точке P0(0;3) есть максимум
Ответ: 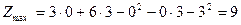
Задача 8.
Найти наибольшее и наименьшее значения функции 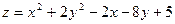 в замкнутом треугольнике АОВ, ограниченном осями координат и прямой x + y -4=0 (рис. 12).
в замкнутом треугольнике АОВ, ограниченном осями координат и прямой x + y -4=0 (рис. 12).
Решение. Чтобы найти наибольшее, и наименьшее значения функции в заданной замкнутой области, необходимо:
1) найти стационарные точки, лежащие внутри области, и вычислить значения функции в этих точках; исследовать на экстремум эти точки не следует;
2) найти наибольшее и наименьшее значения функции на границе области; если граница состоит из нескольких линий, то исследование проводится для каждого участка в отдельности;
3) сравнить полученные значения функции и установить наибольшее и наименьшее значения функции в заданной замкнутой области.
Находим стационарные точки, лежащие внутри заданной области:
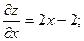
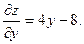
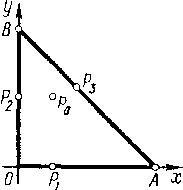
Приравняв нулю частные производные и решив полученную систему
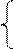
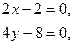
находим стационарную точку Р0(1; 2). Эта точка принадлежит заданной области. Вычислим значение функции в этой точке:
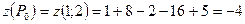
Граница области состоит из отрезка ОА оси Ох, отрезка 0В оси Оу и отрезка АВ. Определим наибольшее и наименьшее значения функции z на каждом из этих трех участков. На отрезке ОА
у = 0, а 0 £ x £ 4. Если у=0, то z(x) = х2 — 2x + 5. Находим наибольшее и наименьшее значения этой функции на отрезке [0, 4]:
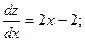
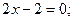
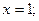
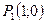
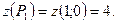
Вычислим значения функции на концах отрезка ОА, т. е. в точках 0(0; 0) и A(4; 0):
z(0) = 5, z(4)= 13.
На отрезке OB х = 0 и 0 £ y £ 4. Если х = 0, то z(y) = 2у 2 -8у + 5. Находим наибольшее и наименьшее значения функции z от переменной у на отрезке [0; 4]:
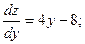
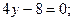
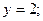
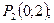
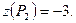
В точке О (0; 0) значение функции уже было найдено. Вычислим значение функции в точке В:
z(В) = z (0; 4) = 5.
Теперь исследуем отрезок АВ. Уравнением прямой АВ будет у = 4 - х. Подставив это выражение- для у в заданную функцию z, получим
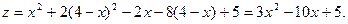
Определим наибольшее и наименьшее значения этой функции на отрезке [0; 4]:
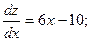
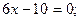
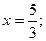
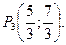
Рз — стационарная точка на отрезке АВ. Вычислим значение функции в этой точке:
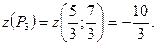
Значения функции на концах отрезка АВ найдены ранее.
Сравнивая полученные значения функции z в стационарной точке Ро заданной области, в стационарных точках на границах области P1, Р2, Рз и в точках О, А и В, заключаем, что наибольшее значение в заданной замкнутой области функция z имеет в точке А, наименьшее значение — в точке Ро(1; 2). Итак,
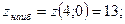
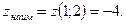
Задача 9. Найти 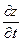 если
если 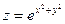 , где x=acost, y=asint.
, где x=acost, y=asint.
Решение:
Речь идёт о дифференцировании сложной функции.
Используя формулу 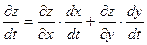 получим
получим 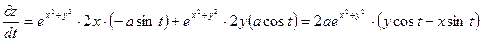
Задача 10.
Исследовать на экстремум функцию z = - 4 + 6x- х2 – ху- у2.
Решение: Чтобы исследовать данную дважды дифференцируемую функцию z = f (x, у) на экстремум, необходимо:
1. Найти частные производные первого порядка 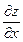 и
и 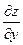 , приравнять их нулю и решить систему уравнений:
, приравнять их нулю и решить систему уравнений: 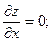
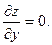
Каждая пара действительных корней этой системы определяет одну стационарную точку исследуемой функции.
Пусть ро (х0 , у0) одна из этих точек.
2. Найти частные производные второго порядка 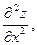
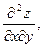
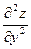 и вычислить их значения в каждой стационарной точке.
и вычислить их значения в каждой стационарной точке.
Положим, что 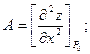
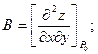
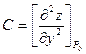
3. Составить и вычислить определитель второго порядка
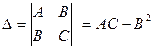
4. Если в исследуемой стационарной точке р0(x0, y0) D>0, то функция z = f(x, у) в этой точке имеет максимум при A<0 и минимум при A>0; если D<0, то в исследуемой точке нет экстремума.
Если D = 0, то вопрос об экстремуме требует дополнительного исследования.
Находим стационарные точки заданной функции:
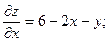
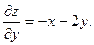
Решение системы 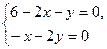 даёт x0= 4, y0= -2.
даёт x0= 4, y0= -2.
Следовательно, данная функция имеет только одну стационарную точку Ро(4, - 2).
Находим частные производные второго порядка и их значения в найденной стационарной точке:
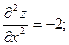
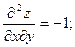
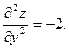
Как видно, частные производные второго порядка не содержат х, они постоянны в любой точке и, в частности, в точке Р0(4, -2). Имеем А = -2; В = - 1; С=- 2.
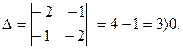
Так как D>0 и A<0, то в точке Ро(4; -2) данная функция имеет максимум:

9.10 Вопросы для самопроверки.
1. Сформулируйте определения функции двух, трёх переменных. Каков геометрический смысл функции двух независимых переменных?
- Что называется областью существования (определения) функции двух переменных?
- Что называется пределом функции двух независимых переменных?
- Сформулируйте определение непрерывности функции двух переменных в точке и в области.
- Что называется частным приращением функции двух переменных? Полным приращением функции двух (нескольких) переменных?
- Дайте определение частной производной функции двух (нескольких) переменных. Укажите геометрический смысл частных производных функции двух переменных.
- Что называется частным дифференциалом функции двух переменных и каков его геометрический смысл?
- Что называется полным дифференциалом функции двух (нескольких) переменных? Каков геометрический смысл полного дифференциала функции двух переменных?
- Сформулируйте правило дифференцирования сложной функции.
- Что называется полной производной и как она находится?
- В чём смысл инвариантности полного дифференциала функции двух (нескольких) переменных?
- Сформулируйте правило дифференцирования неявной функции одной независимой переменной; двух независимых переменных.
- Что называется частной производной второго порядка?
- Сформулируйте теорему о равенстве смешанных частных производных второго порядка.
- Сформулируйте теорему о независимости частной производной высшего порядка от последовательности дифференцирования.
- Дайте определение максимума (минимума) функции двух переменных.
- Сформулируйте необходимые условия экстремума функции двух переменных. Укажите геометрический смысл необходимого признака экстремума функции двух переменных.
- Какие точки называются критическими и как они находятся?
- Сформулируйте достаточные условия экстремума функции двух независимых переменных.
- Укажите способ отыскания наибольшего и наименьшего значения функции двух переменных в заданной замкнутой области.
- Дайте определение производной в данном направлении.
- Что называется градиентом функции двух переменных? Трёх переменных?
- Напишите уравнение касательной плоскости и уравнения нормали к поверхности в данной точке.
- В чём сущность подбора эмпирических формул по способу наименьших квадратов?
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 663; Нарушение авторских прав?; Мы поможем в написании вашей работы!