Основные формулы. Криволинейные интегралы по длине дуги и по координатам

Криволинейные интегралы по длине дуги и по координатам.

Тема 10. Криволинейный интеграл.

Пискунов, гл. XV, § 1-2, упр. 1-5

Данко, гл. II, § 1-4

1. Определение криволинейного интеграла по длине дуги (1-го рода).

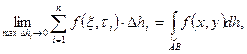
где h=AB, имеющая уравнение y= j(x)

dh-дифференциал дуги ABили h.

2.Вычисление криволинейного интеграла по длине дуги (1-го рода).

где имеющая уравнение y=j(x),

j^/(x)- производная y.

3.Определение криволинейного интеграла по координатам (2-го рода).

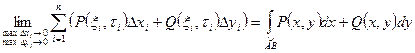
Криволинейный интеграл по координатам (II-го рода) есть работа, совершаемая переменной силой

на криволинейном пути AB(механическое толкование).

4.

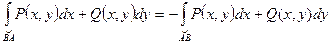
5.

(A C B)

6.Криволинейный интеграл II-го рода (по координатам) вычисляется по формуле:

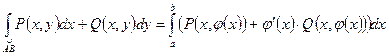
где представлена уравнением y=j(x), [a,b]-отрезок изменения x дуги AB.

7.

т.е криволинейный интеграл по любому замкнутому контуру равен нулю.

8. не зависит от контура интегрирования между т. А и т. В, если выполняется тождественное равенство:

Этот факт используется в качестве наивыгоднейшего пути интегрирования (следует выбрать ломаную, соединяющую точки А и В, звенья которой параллельны осям (OX) и (OY).

Подынтегральное выражение при указанных условиях является полным дифференциалом некоторой однозначной функции т.е а уравнение называется дифференциальным уравнением в полных дифференциалах.

9. Площадь фигуры, ограниченной простым замкнутым контуром С, находится по формуле:

10.2. Примеры решения задач.

Задача 1. Вычислить криволинейный интеграл I-го рода по длине дуги

где L- отрезок прямой от т. O(0;0) до B(4;3)

Решение:

Уравнение прямой имеет вид:

или

Находим тогда

Задача 2. Вычислить площадь фигуры, ограниченной кривыми y= x², x= y²и 8xy=1.

Решение:

Решая совместно уравнения кривых находим координаты точек A и B:

Þ

Þ

Значит, или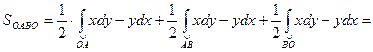

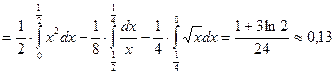
Это краткое решение. Более подробное решение имеет вид:

или

1. -дуга параболы y= x²; dy=2xdx; тогда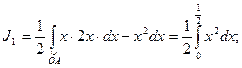

2. - дуга кривой тогда

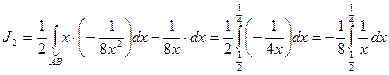
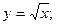
3. -дуга кривой тогда

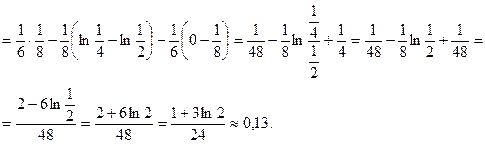
Задача 3. Дано

Проверить, что данное выражение является полным дифференциалом функции «U» и найти эту функцию.

Решение:

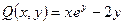
- требование полного дифференциала выполняется и данное

выражение можно записать , где U=U(x,y)- искомая функция.

Будем интегрировать dUпо ломаной OAM(см. рис.)

y. M (x;y)

O(0;0) A(x;0) x

Учтя, что на пути [OA] y=0; dy=0 а на пути [AM] x=const, dx=0, получим:

Ответ:

Задача 4. Найти центр тяжести дуги полуокружности 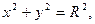лежащей в верхней полуплоскости. Плотность считать равной единице.

Решение: Из соображения симметрии ясно, что центр тяжести лежит на оси (OY), поэтому

X_c=0.

Ордината , где dL-длина дуги.

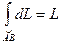- длина полуокружности, т.е

Тогда

Ответ:

Дата добавления: 2014-11-16