Механические и технологические свойства 2 страница

Измерения алмазным конусом с нагрузкой 60кг (HRA) проводят для очень твердых материалов, для твердых поверхностных слоев толщиной 0,3 - 0,5мм или тонких пластинок. (таблица 2.5.)

Измерения стальных шариков с нагрузкой 100кг (HRB) проводят для отожженной стали или отожженных цветных сплавов, с нагрузкой 60кг – (HRF) для свинца, меди.

Расстояния от центра отпечатка до края образца или до центра дру­гого отпечатка должны быть не менее 1,5мм при вдавливании конуса и не менее 4мм при вдавливании шарика. Измерение твердости по Роквеллу требует меньше времени, чем по Бринеллю, результат измерений виден на шкале, кроме того, на поверхности детали остается меньший отпечаток.

Преимуществами метода Роквелла являются простота, высокая производительность, высокая твердость, возможность полной автоматизации и прямой отсчет по шкале; недостатки- необходимость тщательной подготовки измеряемой поверхности, размеры образцов- небольшие.

2.4. Выполнение и оформление результатов работы.

2.4.1. Измерить твердость образцов методом Бринелля и методом Роквелла трижды.

2.4.2. Рассчитать твердость по Бринеллю по формуле.

2.4.3. Методом математической статистики рассчитать ошибку опыта.

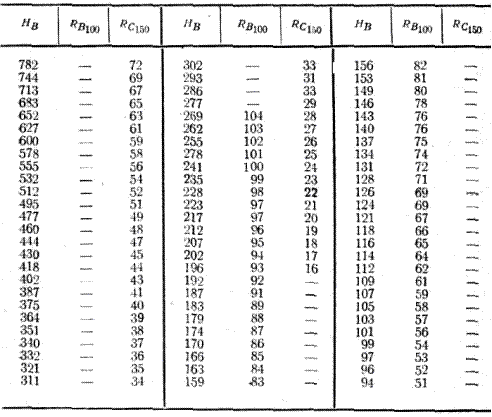
2.4.4. Перевести единицы твердости по Роквеллу в единицы твердости по Бринеллю по таблице 2.6.

Таблица 2.6 Таблица перевода чисел твёрдости

2.4.5. Определить приблизительно по значениям твердости пределы прочности.

2.4.6. Свести все данные в таблице 2.7.

Таблица 2.7. Результаты замера твердости

Метод замера твердости	Диаметр отпечатка, мм	Нагрузка, кг	Шкала	Твердость по Роквеллу	Твердость по Бринеллю
По Бринеллю
По Роквеллу
По Роквеллу

В таблице 2.7 приведены соотношения чисел твердости по Бринеллю с числами твердости по Роквеллу.

2.5. Методика обработки данных измерения

Оценка погрешности измерения в лабораторных условиях производится многократным измерением одной и той же величины. Обычный порядок мате­матической обработки ряда значений измеренной величины сводится к вы­числению параметров распределения случайных погрешностей и оценки этих параметров в следующей последовательности.

2.5.1. Определяется среднее арифметическое значение X из полученных результатов ряда измерений Х₁, Х₂, X₃,..., Х_П,

, (2.5.)

где n- общее число измерения.

2.5.2. Определяются остаточные погрешности V₁, V₂, V₃… V_n, как разности между средним арифметическим значением X и отдельными значениями измеряемой величины X_i:

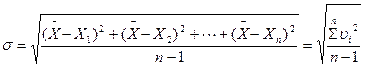(2.6.)

2.5.3. Определяется средняя квадратичная погрешность измерения G.

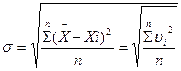
(2.7.)

2.5.4. Определяется предельная погрешность измерения

∆ lim = ± 3G (2.8.)

Если после определения предельной погрешности измерения окажется, что какое-то значение V_i > ∆ lim,то это значение относится к катего­рии "промахов" и должно быть отброшено, после чего производится повтор­ная обработка результатов измерения.

2.5.5. Определяется средняя квадратичная погрешность среднего арифме­тического значения измеряемой величины

(2.9.)

2.5.6. Определяется предельное значение погрешности среднего арифме­тического

(2.10.)

2.6. Контрольные вопросы

1. В чем заключается метод Бринелля для испытания твердости?

2. Что такое число твердости по Бринелю?

3. Какого диаметра шарики применяются для испытания твердости по Бринелю?

4. Какую нагрузку применяют для испытания твердости 10-мм шариком для стали и чугуна?

5. Какую нагрузку применяют при определении твердости для меди, латуни и бронзы?

6. Как расшифровать следующее обозначение: HB _3000/10/30 = 136? HB = 136?

7. Какое время под окончательной нагрузкой следует выдерживать мягкие материалы? Твердые?

8. Можно ли пользоваться прессом Гагарина или другим персом для испытания твердости?

9. Расскажите, как ведется испытание на прессе Бринеля.

10. Почему диаметр лунки следуем измерять по двум взаимно – перпендикулярным направлениям?

11. Какое приближенное соотношение существует между числом твердости по Бринелю и пределом прочности для различных материалов?

12. Чем вызвано создание прибора Роквелла при наличии пресса Бринелля?

13. Какого диаметра шарик применяется в приборе Роквелла?

14. Какую форму имеет алмазный индентор Роквелла?

15. В каких случаях пользуются шариком, а в каких алмазом?

16. Какая нагрузка применяется в приборе Роквелла при пользовании стальным шариком? Алмазным?

17. В каких целях употребляется предварительное надавливание на образец при испытании по Роквеллу?

18. Как производиться испытание на приборе Роквелла?

19. В какое положение устанавливается вращающаяся шкала индикатора после приложения предварительной нагрузки?

20. Как различаются между собой шкалы C и B индикатора?

21. Почему нельзя пользоваться обеими противоположными плоскостями эталонной пластины при проверке прибора Роквелла?

Лабораторная работа 3

Испытание материалов на растяжение

3.1. Цель работы: изучить типы образцов, применяемых для испытания на растяжение; изучить устройство испытательной машины; изучить методику построения и обработки диаграммы растяжения; изучить методику определения показателей прочности и пластичности.

3.2. Теоретическая часть

Самым распространённым способом испытания металлов (после измерения на твердость) является измерение металлов на растяжение. Для этой цели из металла, прочность которого надо установить, изготавливают цилиндрические или плоские образцы, форма и размеры которых указаны в ГОСТе 1497-73 (рис. 3.1)

а – круглый;

б – плоский

Рисунок 3.1. Образцы для испы­тания на растяжение:

При помощи разрывной машины подвергают эти образцы растяжению медленно возрастающей нагрузкой вплоть до разрыва. Испытания выполняют на машинах механического или гидравлического действия. Машины снабжены устройством, позволяющим автоматически фиксировать на диаграмме растяжения величины приложенной нагрузки и изменение длины образца в увеличенном масштабе. Типичный вид такой диаграммы приведен на рис. 3.2.

Рисунок 3.2. Исходная машинная диаграмма. Характеристики, определяемые по диаграмме растяжения.

Из этой диаграммы видно, что в начале растяжения зависимость между удлинением и нагрузкой выражается прямой линией (участок ОА). Это значит, что увеличение нагрузки вызывает пропорциональное увеличение удлинения, т.е. увеличивая нагрузку, например, в два раза, мы получаем увеличение удлинения в два раза. Увеличив нагрузку в три раза, получаем увеличение удлинения также в три раза и т.д. Эта зависимость была впервые установлена ученым Гуком и носит название закона Гука. Закон этот гласит: до некоторого предела изменение нагрузки на образец вызывает пропорциональное изменение длины образца.

Диаграммы растяжения представлены на рис. 3.2. По оси абсцисс от­кладывают абсолютное удлинение образца ∆ℓ, а по оси ординат – силу сопротивления материала Р.

Часто диаграмму растяжения строят в других координатах: по оси абсцисс откладывают относительную деформацию а по оси ординат- напряжение (см. рис. 3.3), где ℓ ₀ - начальная длина образца; F₀ - начальная площадь поперечного сечения образца. Диаграммы, построенные в системе координат P-∆ℓ, называ­ют исходными, а диаграммы, построенные в координатах G-e - условными диаграммами растяжения.

Диаграмму растяжения можно построить в координатах: по оси абсцисс откладывают истинную деформацию 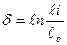, а по оси ординат- истинное напряжение S = 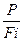(см. рис. 3.4), где 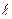_i - удлинение образца в данный момент, F_i - площадь поперечного сечения в данный момент. Такие диаграммы называются истинными диаграммами.

Форма диаграмм растяжения зависит от свойств испытуемого материала.

Рисунок 3.3 Условная диаграмма растяжения

Рисунок 3.4. Истинная диаграмма растяжения

Рисунок 3.5. Диаграмма растяжения для низкоуглеродистых отожженных легированных сталей и цветных металлов (с площадкой текучести)

На рис. 3.5 представлена диаграмма, на которой имеется горизонтальная площадка, соответствующая текучести материала, т.е. продолжению деформации при неизменном сопротивлении материала. Это характерно для низкоуглеродистых, отожженных легированных сталей и цветных металлов. Большинство металлов, в частности, средне- и высокоуглеродистые стали, не обнаруживают такого горизонтального участка на диаграмме растяжения (см. рис. 3.6).

Хрупкие сплавы имеют диаграмму растяжения, представленную на рис. 3.7.

Чаще встречаются диаграммы для сплавов имеющие вид, обозначенный на рис. 3.6.

Для конструкционных материалов важно знать не нагрузку, вызывающую тот или иной характер деформации, а напряжение, определяемое по услов­ной диаграмме растяжения (σ - ε) или рассчитанное по исходной диаграм­ме по формуле

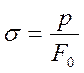(3.1.)

Рассчитываются по формуле (3.2) либо фиксируются по условной ди­аграмме следующие характеристики прочности материала:

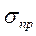- предел пропорциональности металла - напряжение, соответствующее на­чалу отклонения от линейной пропорциональной зависимости между напря­жением и деформацией. Принято считать за предел пропорциональности такое напряжение, при котором отклонение от линейной зависимости между нагрузкой и удлинением достигает такого значения, при котором тангенс угла наклона, образованного касательной к точке P_пц на кривой, увеличивается на 50 % своего значения на линейном упругом участке.

В качестве характеристики прочности конструкционного материала предел пропорциональности используют редко. На этом участке проходит упругая деформация и действует закон Гука:

s = E · e, (3.2.)

где Е - модуль нормальной упругости, модуль Юнга;

ε - относи­тельная деформация, МПа.

Предел упругости, это условное напряжение, при котором остаточная деформация достигает некоторой малой величины 0,01; 0,05 и т.д., т.е. появляются первые признаки макропластической деформации.

Для материалов, имеющих на диаграмме растяжения площадку текучести (см. рис. 3.5), определяют физический предел текучести, как наименьшее напряжение при котором образец деформируется без заметного увеличения растягивающей нагрузки, физический предел текучести обозначается σ_T.

Для большинства конструкционных материалов, не имеющих на диаграмме растяжения площадки текучести, определяется условный предел текучести как напряжение, при котором остаточное удлинение достигает 0,2 % первоначальной длины образца (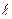 ₀). Условный предел текучести обозначается σ_0.2, МПа;

σ_0.2 = 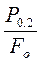(3.3.)

Временное сопротивление (предел прочности) материала - напряжение, соответствующее наибольшей нагрузке P_max, предшествующей разрушению образца. Физический смысл σ_в - сопротивление максимальной равномерной деформации.

При диаграмме растяжения, приведенной на рис. 3.2, 3.4 мы можем определить истинный предел прочности, МПа:

S_в­ = , (3.4.)

где P_В - физический смысл; S_b- сопротивленние максимальной равномерной деформации.

Истинное сопротивление отрыву, МПа:

, (3.5.)

где F_к - конечная площадь поперечного сечения образца в месте шейки.

В случае разрыва хрупких сплавов вид диаграмм растяжения приведен на рис. 3.7 (кривые 1 или 2). В случае диаграммы, отвечающей 1-й кри­вой, мы можем определить четыре характеристики прочности: σ_пц; σ_0.05; σ_0.2;; σ_в.

Истинный предел прочности в этом случае - более строгая характеристика.

Физический смысл σ_в в данном случае - это характеристика предельной прочности.

При ходе диаграммы по 2-й кривой мы не можем определить ни σ_пц ни σ_0.05, ни σ_0.2. Определяем только предел прочности:

Рисунок 3.6. Диаграмма растяжения для средне- и высоко-углеродистой стали (без площадки текучести)

Рисунок 3.7. Диаграммы растяжения для хрупкого сплава

Физический смысл его - это хрупкая прочность, это сопротивление хрупкому разрушению.

Пластические свойства материала оцениваются двумя характеристиками:

1) - относительное удлинение после разрыва - отношение, выраженное в процентах, приращения расчетной длины образца ∆ 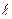, остающееся после разрыва, к его начальной расчетной длине 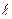о;

2) - относительное сужение - отношение, выраженное в процентах наибольшего уменьшения площади поперечного сечения, образующегося в месте разрыва (∆F) к начальной площади поперечного речения образца (F₀).

Расчет облегчен, если разрыв образца произошел посередине расчет­ной длины образца. Если же разрыв осуществился вблизи головки, расчет относительного удлинения иной.

Как известно, распределение удлинения по расчетной длине образца в процесса растяжения неравномерно. До максимальной нагрузки удлинение развивается равномерно по всей длине образца, а затем начинается мест­ная деформация на участках, где образуется шейка, а также на участках, прилегающих к шейке. Как показано на рисунке 3.8 в случае разрыва образца вблизи головки суммарное удлинение будет меньшим (площади 1+2+3), чем при разрыве образца в середине длины (площади 2+3+4).

Во 2-м образце участок I, расположенный далеко от шейки образца, не участвует в развитии местной деформации, площадь его меньше площади участка 4 в первом образце. Таким образом, величина относительного удлинения будет больше в образце, где разрыв произошел посередине рас­четной длины, и чем дальше от середины расположено место разрыва, том меньше будет относительное удлинение.

В практике для устранения влияния места разрушения на величину относительного удлинения, место разрыва всегда относят к середине рас­четной длины образца и распределяют измеряемое удлинение симметрично по обе стороны от шейки.

На рисунке 3.8. приведен метод подсчета удлинений в случае разрыва образца вблизи головки.

Рис.3.8. Распределение деформации в образце при растяжении

Допустим, что расчетная длина образца равна II участкам по 10мм каждый, ℓ₀ = 110мм, разрыв произошел на 3-м участке. Половинки образца плотно складывают по месту разрыва и измеряют длину шейки 3 и прилегающей к ней участков 1,2 и 4,5, получивших наибольшее удлинение. Обозначим длину этих пяти участков ℓ', число составляющих участков (II -5 = 6) распределяют равномерно относительно места разрыва.

Для этого измеряют длину трех участков 6, 7, 8 - ℓ", не испы­тавших тормозящего действия головок, и полученную длину ℓ" удваивают, перенося, таким образом, участки 9, 10, 11 в левую часть образца и считая их удлинение равным удлинению участков 6, 7 и 8. Тогда длина участков II образца после разрыва:

ℓ_к = ℓ' + 2ℓ" (3.6.)

Таким образом, относительное удлинение в значительной степени яв­ляется величиной условной.

Менее условной характеристикой, которая определяет способность металла деформироваться, является относительное сужение ψ.

3.3. Порядок проведения испытания

Группа делится на восемь бригад, каждая бригада получает I образец

3.1. Измерить начальную длину ℓ₀ и начальный диаметр образца D₀.

3.2. Привести испытание на растяжение и зафиксировать максимальную нагрузку Pb, выдержанную образцом без разрушения. Получить исходную машинную диаграмму растяжения образца в координатах Р-∆ℓ

3.3. Измерить длину образца ℓ-∆ℓ _K после растяжения и диаметр образца в месте формирования шейки D_K.

3.4. По диаграмме определить масштаб записи по оcи абсцисс –

М1 = ∆ℓ - число делений по оси абсцисс.

Рисунок 3.9.Определение масштабов записи по осям диаграммы.

М2 = Pв - число делений по ординате

3.5. Определить по диаграмме P_0,.2или Pm (если есть площадка текучести) и умножить на масштаб

P_0,.2 · М2 (3.7.)

3.6. рассчитать предел текучести, МПа:

σ_0.2 = (3.8.)

3.7. Рассчитать условный предел прочности, МПа:

σ_в = (3.9.)

3.8. Рассчитать относительное удлинение с переносом места разрыва к середине образца и относительное сужение:

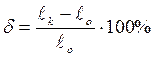; (3.9.)

3.9. Все замеры и полученные данные занести в таблицы. 3.1 и 3.2.

Таблица 3.1. Результаты замера образцов

Размеры образцов	ℓ0, мм	ℓк, мм	Fо, мм	Fк, мм

Таблица 3.2. Результаты расчета исходной диаграммы растяжения

∆ℓ, мм	ε, %	Ψ, %	P0.2, кгс	Pb, кгс	σ0.2, МПа	σв, МПа

3. 4. Требования к отчету

В отчете должны быть представлены исходные диаграммы растяжения (схемы), приведены результаты расчетов, сведены в таблицы. Каждая бригада сохраняет диаграмму растяжения.

Диаграммы растяжения и результаты должны быть сопоставлены. Проанализировать влияние места разрыва образца на величину относительного удлинения.

3.5. Контрольные вопросы:

1. Какие виды диаграмм растяжения вы знаете?

2. Что такое предел пропорциональности и как он определяется?

3. Что такое предел упругости сплава и как он определяется?

4. Что такое предел текучести сплава и как он определяется?

5. Чем отличается физический «предел текучести от условного?

6. Что такое предел прочности условный, истинный, как они определяются?

7. Что такое сопротивление отрыву?

8. Каковы единицы измерения напряжения?

9. Что такое исходная, условная и истинная диаграмма растяжения?

I0.Что такое относительные сужение и удлинение, единицы их измерения?

11.Что такое истинное удлинение, как оно подсчитывается?

12.Физические смысл пределов прочности в случае растяжения хрупкого об разца сплава, и абсолютно хрупкого?

13.Какую зависимость выражает кривая на отдельных первичных диаграмм?

14.В чем смысл закона Гука?

15.Какая точка кривой растяжения соответствует началу образования шейки в образце?

16.Какая из двух нагрузок больше - нагрузка текучести или нагрузка, при которой начинает образовываться шейка в образце?

17.Допустима ли остановка в нагружении образца или разгрузка машины после того, как был превзойден предел текучести?

Лабораторная работа 4.

Связь прочностных и пластических свойств металлов при растяжении с размером зерна и плотности дислокаций

4.1. Цель работы: исследовать влияния размера зерна и плотности дислокаций на прочностные и пластические свойства при растяжении.

4.2. Теоретическая часть

Размер зерна, плотность дислокаций оказывают существенное влияние на механические свойства металлов и сплавов.

Предел текучести связан с диаметром зерна (D) известным уравнением Холла-Петча:

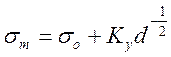, (4.1)

где (σ₀ - напряжение, необходимое для перемещения дислокаций внутри зерна; K_y - коэффициент, определяющий трудность передачи деформации от зерна к зерну. Физический смысл произведения K_y d^-1/2 заключается в том, что оно характеризует напряжение, необходимое для инициирования работы дислокационных источников в соседних зернах. Урав­нение (4.1) выполняется и для условного предела прочности многих сплавов с различной структурой.

Если сплав подвергался холодной пластической деформации, в нем возрастает плотность дислокаций и напряжения в металле возрастают, т.е. возрастает предел упругости, предел текучести и предел прочности. Зависимость при этом определяется выражением:

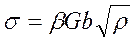(4.2)

где G - предел упругости;

β - коэффициент, зависящий от природы металла;

ρ - плотность дислокаций;

b – вектор Бюргерса.

Особенно чувствительными к плотности дислокаций являются прочностные характеристики (предел упругости и предел текучести). В то же время временное сопротивление разрушению (условный предел прочности σ_b) мало зависит от исходной плотности дислокаций, так как к моменту достижения σ_b плотность дислокаций за счет деформационного упрочнения становиться вне зависимости от исходной, очень большой.

4.3. Порядок выполнения работы

4.3.1. Провести испытание двух образцов одной и той же марки стали с разным размером зерна, в отожженном состоянии, третий образец из той же стали продеформировать на 5 %. четвертый- на 10 %, снять нагрузку и испытать повторно на растяжение.

4.3.2. По исходным машинным диаграммам определить

σ_0,2 и σ_b, δ и ψ.

4.3.3. Приготовить шлифы для металлографического анализа (в головке образца) и определить средний линейный размер зерна:

S = 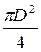, (4.3.)

где S - площадь зерна, мм²;

D - диаметр зерна, подсчитанный с помощью окуляр-микрометра по формуле:

D = 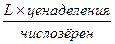, (4.4.)

где L - интервал линейки.

4.3.4. По своим экспериментальным и выданным преподавателем данным δ, σ_0.2, σ_b и D построить зависимости механических свойств от размера зерна и определить коэффициенты уравнения Холла-Петча.

4.3.5. Измерить плотность дислокаций ρ в образцах после предваритель­ного растяжения на 5 и 10 % по выданным электронным снимкам.

4.3.6. Проанализировать влияние D и ρ на σ_0.2 и σ_в.

4.4. Требования к отчету

В отчете по работе должны быть представлены:

- построенные кривые формации образцов с различным размером зерна и плотностью дислокаций;

- графическая зависимость σ_0.2 и σ_в от среднего значения размера зерна и от плотности дислокаций в предварительно растянутых образцах;

- график изменения механических свойств сплава в зависимости от плотности дислокаций;

- выводы по полученным зависимо­стям.

4.5. Контрольные вопросы

1. Как зависит предел текучести σ_0.2 от размера зерна?

2. Почему измельчение зерна приводит к упрочнению?

3. Каков физический смысл напряжения σ_i в уравнении Холла-Петча?

4. Что характеризует K_y в уравнении Холла-Петча?

5. Как влияет плотность дислокаций на σ_0.2?

6. Как влияет плотность дислокаций на σ_0.2?

7. Почему с увеличением плотности дислокаций растут некоторые прочностные свойства?

6. Какое свойство σ_0,05 или σ_0.2 увеличится больше при повыше­нии исходной плотности дислокаций на 50 %?

9. Как влияет размер зерна и плотность дислокаций на пластические свойства?

Дата добавления: 2014-11-16