Краткая теория. «Определение скорости распространения звука

Лабораторная работа №5.

«Определение скорости распространения звука

методом стоячих волн»

В сплошной реальной среде частицы вещества связаны между собой упругими силами. При выведении частицы из положения равновесия на нее будут действовать силы, стремящиеся возвратить ее обратно в это положение. Под действием этих сил частица приобретает кинетическую энергию и по инерции пройдет через положение равновесия, т.е. придет в колебательное движение (см. работу 4). Её колебания будут с некоторым опозданием передаваться соседним частицам и процесс будет распространяться в пространстве. Процесс распространения колебаний в окружающей среде называется волновым процессом ли волной. Волна графически изображается так же, как и колебание, т.е. синусоидой.

Если колебания происходят перпендикулярно направлению распространения колебаний, то волна называется поперечной. Если колебания происходят вдоль направления распространения колебаний, то волна называется продольной.

Расстояние (по направлению распространения волны) между двумя ближайшими точками, которые колеблются в одной фазе, называется длиной волны. Длинна волны 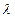, период Т, частота 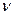и скорость u распространения волны связаны простыми зависимостями:

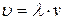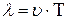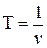; ; ; (1)

Скорость распространения волн зависит от свойств среды, в которой они распространяются. Для газов ;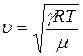

где 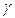- показатель степени адиабаты, R- универсальная газовая постоянная, равная 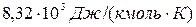, Т- температура в кельвинах. Для воздуха

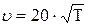м/с (2)

Если колебание источника (вибратора), находящегося в точке Р (рис.1) определяется уравнением 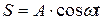, то колебание точки М, находящейся на расстоянии x от начала координат, определяется уравнением:

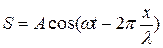, (3)

которое называют уравнением бегущей волны. Вид уравнения показывает, что колебание точки М повторяет колебания точки Р, но сдвинутого по фазе на величину 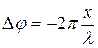. Важно отметить, что сдвиг фаз 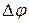определяется не абсолютным значением величины 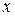, а отношением 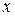к

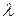, так как изменение фазы на 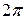величины синуса не изменяет. Пусть две

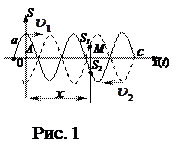волны одного периода и одинаковой амплитуды идут навстречу друг другу с одинаковой скоростью.

Смещение S в точке М (рис.1) от каждой волны будет определяться уравнениями:

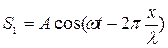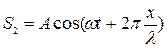; (4)

Принимаем, что первая волна (сплошная линия) распространяется в направлении от точки Р к точке С, а вторая волна (пунктирная линия) – от точки С к точке Р. Поэтому во втором равенстве перед начальной фазой, в отличии от первого равенства, стоит противоположный знак (положительный). Складывая эти колебания, получим уравнение определяющее колебания точки М:

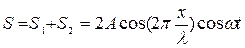(5)

Это есть уравнение стоячий воды. Здесь S -смещение колеблющейся точки, находящейся на расстоянии 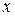от О. Из уравнения (5) следует:

1) колебание является гармоническим и имеет тот же период, что и у встречных волн:

2) амплитуда колебания, равная

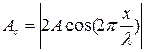(6)

зависит от положения точек М, т.е. от значения 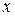, и не зависит от времени.

Дата добавления: 2014-11-16