Примеры решения задач. Задача 1. Кинематическое уравнение движения точки вдоль оси Х имеет вид

Задача 1. Кинематическое уравнение движения точки вдоль оси Х имеет вид 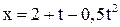. Найти координату, скорость и ускорение точки в момент времени .

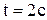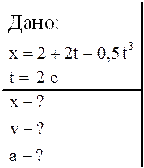
Решение:

Скорость есть первая производная от координаты по времени .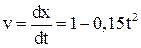

Ускорение первая производная от скорости по времени .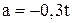

Подставляя численные значения, получим:

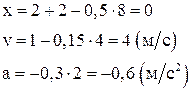
Ответ: .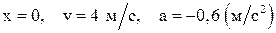

Задача 2. Движение точки по окружности радиуса 0,1 м описывается уравнением 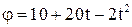. Для момента времени 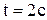определить тангенциальное, нормальное и полное ускорение точки.

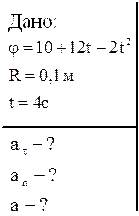
Решение:

По определению угловая скорость есть первая производная от угла поворота по времени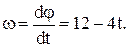

Угловое ускорение производная от угловой скорости .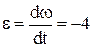

Тангенциальное ускорение связано с угловым ускорением 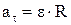, а нормальное ускорение .

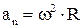Полное ускорение точки .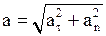

Подставляя численные значения найдем: , , .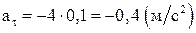

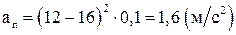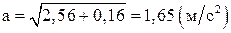Ответ: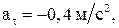

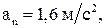
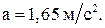
Задача 3. Наклонная плоскость длиной 2 м образует угол 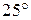с горизонтом. Тело, двигаясь равноускоренно, соскальзывает с этой плоскости за 2 с. Определить коэффициент трения тела о плоскость.

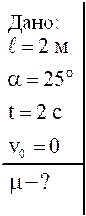
Решение:

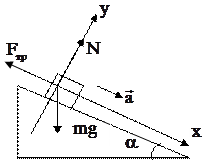На тело действуют сила тяжести 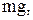сила реакции опоры 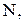сила трения 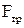. По второму закону Ньютона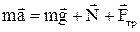

В проекции на оси координат получим

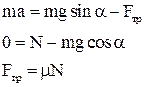
Решая полученную систему уравнений, найдем ускорение тела

.

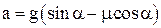При равноускоренном движении без начальной скорост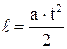и или 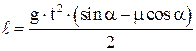. Отсюда 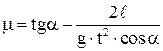. Подставляя численные значения найдем .

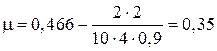Ответ: .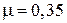

Задача 4. В баллоне объемом 25 л

находится водород при температуре 290 К. После того как часть водорода израсходовали, давление в баллоне уменьшилось на 0,4 МПа. Определить массу израсходованного водорода

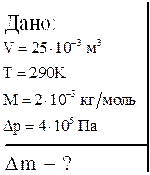Решение:

Массу израсходованного водорода можно найти по формуле 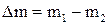. Массу водорода в баллоне можно найти из уравнения Менделеева – Клапейрона 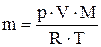и тогда 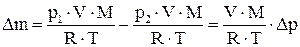. После вычислений найдем .

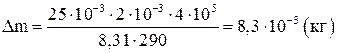Ответ: .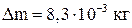

Задача 5. Кислород при неизменном давлении 80 кПа нагревается так, что его объем увеличивается от 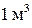до 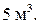Определить: изменение внутренней энергии кислорода; работу совершенную им и количество теплоты, переданного газу.

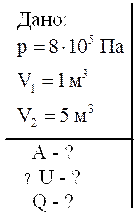Решение:

Работа газа при изобарическом расширении определяется по формуле .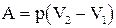

Изменение внутренней энергии

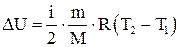. Выражая температуру газа из уравнения Менделеева-Клапейрона 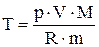получим, 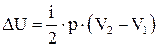. Разделив полученные равенства, найдем 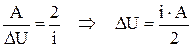. Из первого начала термодинамики 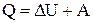будем иметь .

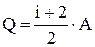Ответ: , , .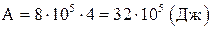

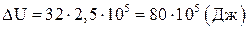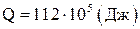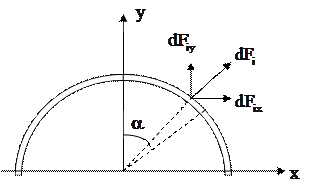
Задача 6. По тонкому проводу в виде кольца радиусом 20 см течет ток 100 А. Перпендикулярно плоскости кольца возбуждено магнитное поле с индукцией 0,02 Тл. Определить силу, растягивающую кольцо.

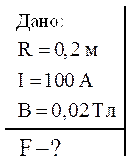Решение:

Рассечем кольцо на две равные части и найдем силу, действующую на одну из них. Выделим на проводе элемент длиной .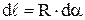

На этот элемент по закону Ампера будет действовать сила

.

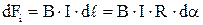И тогда можно утверждать, что .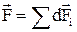

Разложим вектор 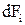на составляющие 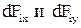и тогда в силу симметрии задачи, можно утверждать, что 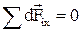и 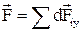. Так как все составляющие 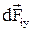направлены в одну сторону, то геометрическое сложение можно заменить алгебраическим и тогда .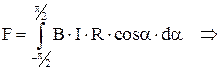

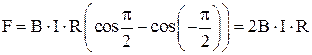Вычисляя, найдем .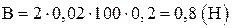

Ответ: .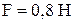

Задача 7. Электрон, пройдя ускоряющую разность потенциалов 400 В, попадает в однородное магнитное поле с индукцией 0,01 Тл. Определить: радиус окружности, по которой будет двигаться электрон; период обращения электрона. Вектор скорости электрона перпендикулярен линиям индукции магнитного поля.

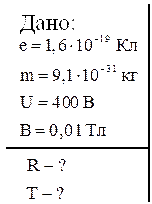
Решение:

На электрон, движущийся в магнитном поле, будет действовать сила Лоренца 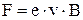, но по второму закону Ньютона 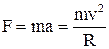и, тогда, .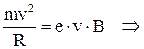

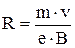Кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов, определяется равенством 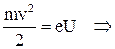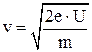и тогда 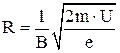. Для определения периода обращения воспользуемся формулой 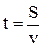и, следовательно, .

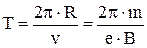Вычисляя, найдем , .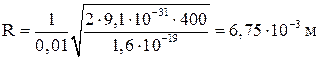

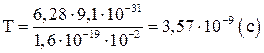Ответ: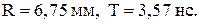

Задача 8. Луч света падает на плоскопараллельную стеклянную пластинку (п = 1,6) под углом i = 45º. Определить толщину пластинки, если вышедший из пластинки луч смещен относительно продолжения падающего луча на расстояние h = 2 см.

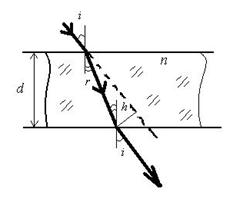
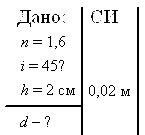
Решение:

Вышедший из пластинки луч будет параллелен падающему (ход лучей показан на рис.). Из рисунка следует, что

,

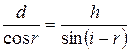откуда 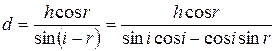. (1)

Согласно закону преломления, 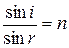, откуда 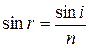. Подставив это значение в формулу (1), а также выразив косинус угла через синус, найдем искомую толщину пластинки:

.

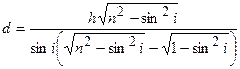Ответ: d = 5,58 см.

Задача 9. Определить разность показателей преломления обыкновенного и необыкновенного лучей, если наименьшая толщина кристаллической пластинки в четверть волны для 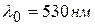составляет .

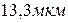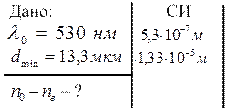
Решение: Пластинкой в четверть волны называется вырезанная параллельно оптической оси пластинка, для которой оптическая разность хода

,

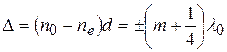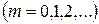
причем знак плюс соответствует отрицательным кристаллам, минус – положительным. При прохождении через эту пластинку в направлении, перпендикулярном оптической оси, обыкновенный и необыкновенный лучи, не изменяя своего направления, приобретают разность хода, равную 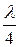. Минимальная толщина пластинки в четверть волны соответствует 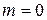. Тогда 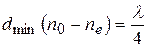, откуда .

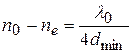Ответ: .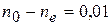

Дата добавления: 2014-11-16