
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные понятия теории фильтров
Выбор схемы и параметров активного фильтра
Электрический фильтр – устройство для выделения желательных компонентов спектра электрического сигнала и/или подавления нежелательных.
Активным фильтром называют такой, в котором присутствует один или несколько активных компонентов, к примеру, транзистор или операционный усилитель. В данной курсовой работе все фильтры строятся на базе ОУ.
Все фильтры характеризуются зависимостью коэффициента передачи от частоты, называемой амплитудно-частотной характеристикой (АЧХ) фильтра.
По виду частотной характеристики фильтры подразделяются на:
- фильтры нижних частот (ФНЧ). Это фильтры, пропускающие частотный спектр сигнала ниже некоторой частоты, которая называется частотой среза 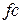 , и уменьшающие (подавляющие) частоты сигнала выше этой частоты. Степень подавления каждой частоты зависит от вида фильтра.
, и уменьшающие (подавляющие) частоты сигнала выше этой частоты. Степень подавления каждой частоты зависит от вида фильтра.
- фильтры верхних частот (ФВЧ). Это фильтры, пропускающие высокие частоты входного сигнала, при этом подавляя частоты сигнала меньше, чем частота среза. Степень подавления зависит от конкретного типа фильтра;
- полосно-пропускающие фильтры (ППФ). Фильтры, которые пропускают сигналы с частотой, находящейся в некоторой полосе частот 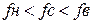 ;
;
- полосно-задерживающие (режекторные) фильтры (ПЗФ). Фильтры, которые задерживают сигналы с частотой, находящейся в некоторой полосе частот 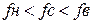 ;
;
- фазовые фильтры. Это фильтры, пропускающие все частоты сигнала с равным усилением, однако изменяющие фазу сигнала. В нашей курсовой работе такие фильтры не применяются.
Наиболее полно исследованы фильтры нижних частот. От них легко перейти к другим видам фильтров. Идеальный ФНЧ практически нереализуем. Он имеет прямоугольную форму АЧХ, которая иногда в литературе называется «кирпичной стеной» (рисунок 3.4, а). Но существует несколько аппроксимаций (настроек) идеального фильтра, исследованных различными учеными и носящих их имена.
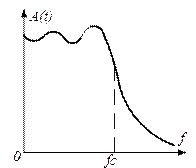
Фильтры Баттерворта – это наиболее употребительные фильтры с максимально плоской формой АЧХ. Подобные фильтры были впервые описаны британским инженером Стефаном Баттервортом в статье «О теории фильтрующих усилителей», в журнале Wireless Engineer в 1930 году. Они имеют достаточную крутизну скатов и приемлемо пропускают импульсные сигналы.
АЧХ фильтра Баттерворта показана на рисунке 3.4, б.
Фильтры ЧебышеваI рода имеют крутизну скатов АЧХ большую, чем фильтры Баттерворта, но имеют существенные пульсации амплитудно-частотной характеристики на частотах полос пропускания, чем у фильтров других типов. Фильтр получил название в честь известного русского математика XIX века Пафнутия Львовича Чебышева, так как характеристики этого фильтра основываются на многочленах Чебышева.
АЧХ фильтров Чебышева I рода показана на рисунке 3.4, в.
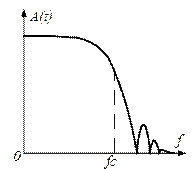
Фильтры Чебышева II рода, или инверсные фильтры Чебышева. Эти фильтры имеют плоскую АЧХ в полосе пропускания, подобную фильтру Баттерворта, но существенные пульсации амплитудно-частотной характеристики на частотах полос подавления.
Фильтры Чебышева обычно используются там, где требуется с помощью фильтра небольшого порядка обеспечить требуемые характеристики АЧХ, в частности, хорошее подавление частот из полосы подавления, и при этом гладкость АЧХ на частотах полос пропускания и подавления не столь важна. АЧХ фильтров Чебышева II рода показана на рисунке 3.4, г.
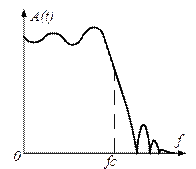
Фильтры Чебышева-Кауэра, или эллиптические фильтры (иногда также называемые полными фильтрами Чебышева, двойными Чебышева, фильтрами Дарлингтона или Золотарёва) обладают колебаниями коэффициента передачи, как в полосе пропускания, так и в полосе задерживания. Здесь быстро достигается заданное затухание за пределами полосы пропускания и сохраняется его минимальное значение на нежелательных частотах. Аналогично инверсным фильтрам Чебышева на определённых частотах в полосе задерживания они имеют бесконечное затухание.

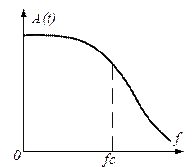
а б в
г д е
Рисунок 3.4 – АЧХ фильтров нижних частот: а –идеальный фильтр; б – фильтр Баттерворта; в – фильтр Чебышева I рода; г – фильтр Чебышева II рода; д - эллиптический фильтр; е – фильтр Бесселя
Для аппроксимации амплитудно-частотной характеристики идеального фильтра по числу элементов цепи эллиптические фильтры, по-видимому, наиболее эффективны. При заданном порядке функции имеется возможность создать наиболее экономичный фильтр либо с очень крутой переходной областью, либо с очень высоким затуханием в полосе задерживания. С другой стороны, само затухание не спадает монотонно к бесконечному значению за пределами полосы затухания, а сохраняется на заранее обусловленном уровне. Следует отметить, что фильтры Чебышева и инверсные Чебышева представляют собой частные случаи более общих фильтров Чебышева-Кауэра.
АЧХ фильтров Чебышева-Кауэра показана на рисунке 3.4, д.
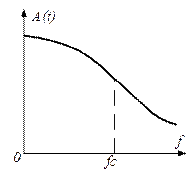
Фильтры Бесселя – применяются для передачи импульсных сигналов, так как форма сигналов, которые проходят через фильтр, остается практически неизменной.
АЧХ фильтров Бесселя показана на рисунке 3.4, е.
Схемная реализация АЧХ рассмотренных фильтров, осуществляется с помощью активных фильтров, состоящих из ОУ и пассивных элементов R и C.
Для анализа фильтров используется понятие передаточной функции. Это отношение изображений по Лапласу выходного 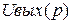 и входного
и входного 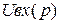 напряжений:
напряжений:
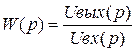 . (3.12)
. (3.12)
Передаточные функции фильтров могут быть разложены на сомножители 1-го и 2-го порядка.
В случае четного порядка фильтра n, передаточные функции полиномиальных фильтров: Баттерворта, Чебышева I рода и Бесселя - приобретают вид
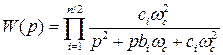 , (3.13)
, (3.13)
где 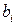 ,
, 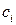 - безразмерные коэффициенты.
- безразмерные коэффициенты.
Для неполиномиальных фильтров – инверсного фильтра Чебышева и эллиптического, получаем
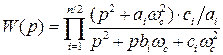 , (3.14)
, (3.14)
где 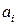 ,
, 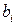 ,
, 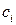 - безразмерные коэффициенты.
- безразмерные коэффициенты.
Задавая значения коэффициентов в выражениях (3.11) и (3.12), можно получать АЧХ фильтров различных аппроксимаций.
В таблице 3.2 приведены эти коэффициенты для некоторых фильтров 2-го, 4-го и 6-го порядка.
В таблице 3.2 приняты обозначения:
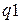 - уровень минимумов пульсаций АЧХ в полосе пропускания (уровень максимумов принят за 0 дБ). Значение 0,5 дБ соответствует отклонению от 100% примерно на 5,5%; 1 дБ – 10,9%; 2 дБ – 20,6%;
- уровень минимумов пульсаций АЧХ в полосе пропускания (уровень максимумов принят за 0 дБ). Значение 0,5 дБ соответствует отклонению от 100% примерно на 5,5%; 1 дБ – 10,9%; 2 дБ – 20,6%;
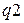 - уровень максимумов пульсаций АЧХ в полосе задерживания, дБ. Уровень минус 40 дБ соответствует 1%.
- уровень максимумов пульсаций АЧХ в полосе задерживания, дБ. Уровень минус 40 дБ соответствует 1%.
Для получения фильтров высоких порядков (четных) следует использовать соединенные последовательно звенья фильтров 2-го порядка.
Таблица 3.2 – Коэффициенты аппроксимации фильтров
| Порядок фильтра | |||||||
| Номер звена | |||||||
| Тип фильтра | Коэф. | Значения коэффициентов | |||||
| Баттерворта | b c | 1,4142 1,0000 | 0,7654 1,0000 | 1,8478 1,0000 | 0,5176 1,0000 | 1,4142 1,0000 | 1,9319 1,0000 |
Чебышева I
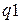 =0,5 дБ =0,5 дБ
| b c | 1,4256 1,5162 | 0,3507 1,0635 | 0,8467 0,3564 | 0,1553 1,0230 | 0,4243 0,5900 | 0,5796 0,1570 |
Чебышева I
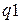 =1 дБ =1 дБ
| b c | 1,0977 1,1025 | 0,2791 0,9865 | 0,6737 0,2794 | 0,1244 0,9907 | 0,3398 0,5577 | 0,4641 0,1247 |
Продолжение таблицы 3.2
Чебышева I
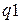 =2 дБ =2 дБ
| b c | 0,8038 0,8231 | 0,2098 0,9237 | 0,5064 0,2216 | 0,0939 0,9660 | 0,2567 0,5329 | 0,3506 0,0999 |
Чебышева II 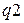 =-40 дБ =-40 дБ
| a b c | 100,99 1,4141 1,0099 | 4,7485 0,6892 1,0375 | 27,676 2,0315 1,2667 | 2,1487 0,3791 1,0346 | 4,0094 1,3338 1,3323 | 29,927 2,5582 1,8705 |
Эллиптический
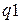 =0,5 дБ =0,5 дБ
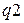 =-40 дБ =-40 дБ
| a b c | 143,63 1,4180 1,5214 | 3,0091 0,9071 0,4478 | 14,910 0,2719 1,0614 | 1,3095 0,7701 0,3176 | 9,9655 0,3058 0,7965 | 1,8557 0,0650 1,0142 |
| Бесселя | b c | 3,0000 3,0000 | 5,7924 9,1401 | 4,2076 11,488 | 6,0319 26,514 | 8,4967 18,801 | 7,4714 20,853 |
|
|
Дата добавления: 2014-11-18; Просмотров: 2151; Нарушение авторских прав?; Мы поможем в написании вашей работы!