Фильтры нижних частот

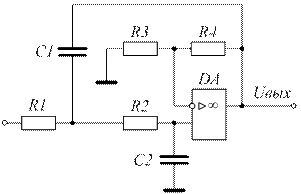
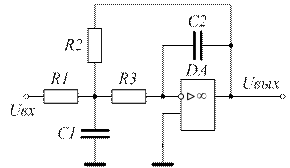
Чаще других применяют две схемы, изображенные на рисунке 3.5, а и 3.5, б.

Схему на рисунке 3.5, а называют фильтром с положительной обратной связью или схемой Саллена-Кея, (или Саллена-Ки), а схему на рисунке 3.5, б называют фильтром со сложной отрицательной обратной связью или схемой Рауха.

Для схемы Саллена-Кея передаточная функция имеет вид

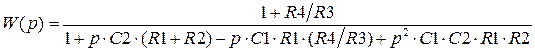. (3.15)

Для схемы Рауха передаточная функция будет такова

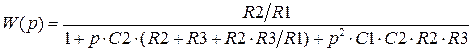. (3.16)

а б

Рисунок 3.5 – Схемы ФНЧ 2-го порядка: а – Саллен-Кея; б - Рауха

Схемы Саллен-Кея и Рауха пригодны только для реализации полиномиальных фильтров: Баттерворта, Чебышева I рода и Бесселя.

Более универсальная, хотя и более сложная схема ФНЧ приведена на рисунке 3.6. Это так называемое – биквадратное звено. В ней при условии, что 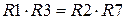, клемму 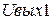можно использовать как выходное напряжение звена эллиптического фильтра или инверсного фильтра Чебышева.

То есть, это звено позволяет реализовывать неполиномиальные фильтры 2-го порядка.

Если же 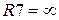и 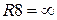, то выходная клемма 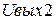соответствует звену 2-го порядка фильтров Баттерворта, Чебышева I рода и Бесселя. Биквадратное звено менее чувствительно к неточности элементов и проще в настройке.

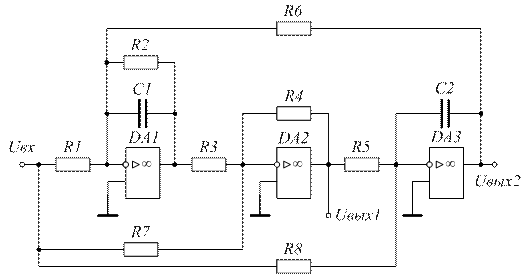
Рисунок 3.6 – Схема биквадратного звена (реализация неполиномиальных фильтров 2-го порядка по выходу )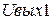

Для биквадратного звена передаточные функции в зависимости от выходной клеммы будут такими

,

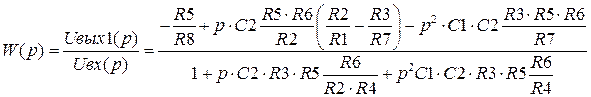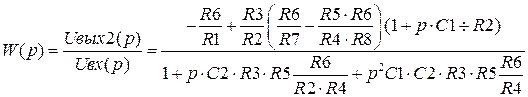. (3.17)

Общий метод расчета ФНЧ с указанными схемными реализациями следующий:

- исходными данными для расчета являются частота среза фильтра 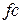и коэффициент усиления фильтра .

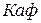- выбираем базовую схему фильтра 2-го порядка. Для полиномиальных фильтров берем схему Саллена –Кея или схему Рауха. Для неполиномиальных - биквадратное звено;

- по расчетным формулам (приведенным ниже) определяем значения всех резисторов и конденсаторов. Получив значение элемента, сразу округляем его до ближайшего номинального значения по таблице 3.1. Используем ряд Е25. Во всех расчетах, кроме пунктов 1 и 2, во всех формулах используется система СИ. Все величины емкостей подставляются в Фарад, все величины сопротивлений в Ом. Учитываем, что 1 Ф = 10⁶ мкФ или 1 мкФ = 10^-6 Ф;

- если фильтр имеет 4-й или 6-й порядок, включаем последовательно второе (для 4-го) и третье (для 6-го) звенья. Коэффициенты 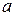, , 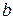и 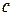для каждого звена берем из таблицы 3.2, где указаны эти коэффициенты для 1-го, 2-го и 3-го звена. Каждое звено рассчитывают по своим коэффициентам и в том порядке, в котором они указаны в таблице 3.2 друг за другом последовательно включают в схему.

Дата добавления: 2014-11-18