Узкополосные полосовые пропускающие фильтры

Узкополосными считают фильтры, у которых 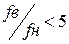. Создание узкополосных полосовых пропускающих фильтров (УППФ) сложнее, чем широкополосных.

Например, такой фильтр 4-го порядка состоит из двух последовательно включенных звеньев второго порядка со взаимной расстройкой.

Исходными данными для расчета являются частоты нижней 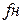и верхней границ полосы пропускания. Для упрощения расчетов будем рассматривать схему фильтра, в котором общий коэффициент усиления фильтра 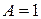, то есть для данного типа фильтра следует при распределении усиления по каскадам принять .

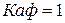Следует отметить, что коэффициенты усиления отдельных звеньев, входящих в состав фильтра, могут иметь коэффициенты усиления отличные от единицы.

Методика расчета данного фильтра состоит из следующих этапов.

1. Определяем среднюю частоту диапазона пропускания

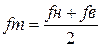. (3.38)

2. Определяем относительное значение полосы пропускания

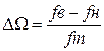. (3.39) 3. Составляем уравнение для определения параметров звеньев фильтра

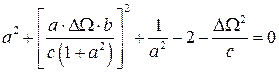, (3.40)

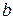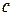где и - коэффициенты из таблицы 3.2, в соответствии с видом аппроксимации разрабатываемого фильтра.

Решаем полученное уравнение относительно параметра 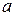. Численное решение уравнения (3.40) можно выполнить любым способом.

Уравнение (3.40) имеет 8 корней. Но нас интересует только один корень со значением близким к 1. Для практических целей достаточно определить этот корень с точностью до третьего знака после запятой.

4. Находим добротность фильтра

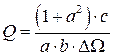. (3.41)

5. Определяем основные параметры последовательно включенных звеньев фильтра

Таблица 3.3 – Параметры звеньев УППФ

Звено фильтра

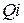
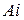
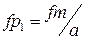
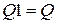
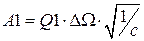
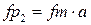
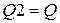
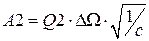
Для реализации УППФ можно использовать несколько схем. Одна из них, широко применяемая на практике, приведена на рисунке 3.9.

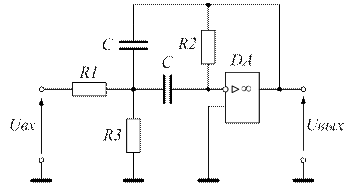
Рисунок 3.9 – Полосовой пропускающий фильтр со сложной отрицательной обратной связью

Дата добавления: 2014-11-18