Решение. Примеры решения задач

Примеры решения задач

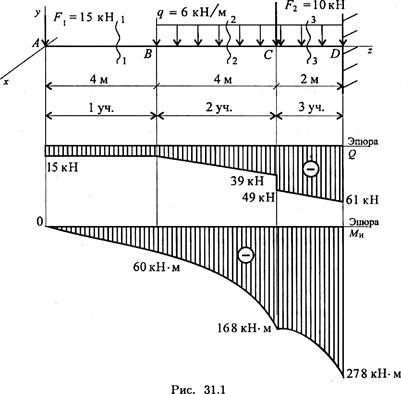
Пример 1. Одноопорная балка нагружена сосредоточенными силами и распределенной нагрузкой (рис. 31.1). Построить эпюры поперечных сил и изгибающих моментов.

Задачу решаем с помощью составления уравнений поперечных сил и изгибающих моментов в поперечных сечениях балки.

При проверке эпюр используем дифференциальные зависимости между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом:

1. Производная от поперечной силы по длине балки равна ин­тенсивности распределенной нагрузки

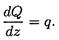
2. Производная изгибающего момента по длине балки равна по­перечной силе

Рассмотрим участок 1, сечение 1. Поперечная сила Q₁ = - F₁ = —15 кН.

По принятому правилу знаков поперечная сила отрицательна и постоянна на этом участке.

Изгибающий момент M_Xl = — F₁ z₁.

0 ≤ z₁ ≤ 4м: М_А = 0; М_В = -15*4 = - 60кН*м.

Рассмотрим участок 2, сечение 2. Поперечная сила

Q₂ = — F₁ — q(z₂ — 4).

4м ≤ z₂ ≤ 8м:

Q_B = - F₁ = -15кН;

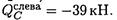
Поперечная сила изменяется по линейному закону.

Изгибающий момент

:

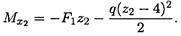
4м ≤ z₂ ≤ 8м:

при z₂ = 4м изгибающий момент М_В = — 60кН • м. В точке В нет внешнего момента, поэтому изгибающий момент слева и справа от точки В одинаков. В этом случае рассчитывать его дважды не следует;

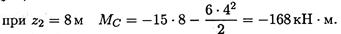
Рассмотрим участок 3, сечение 3.

В точке С приложена внешняя сила F ₂. На эпюре должен быть скачок, равный приложенной силе; на эпюре моментов должен быть излом.

Поперечная сила на участке 3: Q₃ = —F₁ — q(z₃ — 4) — F₂;

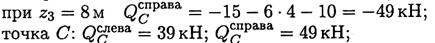
при z₃ = 10 м Q_D = -15 – 6*6 - 10 = - 61 кH.

Поперечная сила изменяется по линейному закону.

Изгибающий момент.

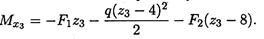
8 м ≤ z₂ ≤ 10 м:

при z₃ = 10 м

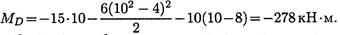
На участках 2 и 3 эпюра изгибающих моментов ограничена квад­ратичной параболой.

По полученным результатам, учитывая дифференциальные за­висимости между поперечной силой и изгибающим моментом, стро­им эпюры Q и М_х. На втором и третьем участках поперечная сила не имеет нулевых значений, поэтому на эпюре моментов нет экс­тремумов.

Основные правила построения эпюр в случае приложения распределенной нагрузки. Контроль правильности решений.

1. Для участка балки с равномерно распределенной нагрузкой поперечная сила Q изменяется по линейному закону, эпюра ограни­чена наклонной прямой. Изгибающий момент изменяется по квадра­тичному закону, эпюра М_х ограничена параболой второго порядка.

2. В сечении, где эпюра Q переходит через ноль (наклонная ли­ния пересекает ось абсцисс), изгибающий момент экстремален: каса­тельная к эпюре М_х в этом месте параллельна оси абсцисс.

3. Параболическая и прямолинейная части эпюры моментов там, где кончается или начинается распределенная нагрузка, сопрягают­ся плавно, без излома, если в соответствующем сечении к балке не приложена сосредоточенная сила.

4. Если распределенная нагрузка направлена вниз, то эпюра мо­мента очерчена параболой, обращенной выпуклостью вверх.

5. Из теоремы Журавского следует:

— если на участке Q > О, М_и растет;

— если на участке Q < О, М_и убывает;

— если на участке Q = 0, изгибающий момент постоянен (чистый изгиб);

— если в точке Q = 0, изгибающий момент достигает экстре­мального значения (М_и ^miп или М_и ^мах).

Пример 2. Расчет двухопорной балки. Двухопорная балка на­гружена равномерно распределенной нагрузкой (рис. 31.2).

Дата добавления: 2014-11-18