Розрахунок стержневих систем

Щодо виконання лабораторних робіт

МЕТОДИЧНІВКАЗІВКИ

([phone]

НАЧНИТЕ УЖЕ СЕГОДНЯ!

Литература

1. БаловсякН.В. ВидеосамоучительOffice 2007 (+CD). – СПб.:Питер,2008. – 320с.: - ил.

2. Безручко В.П. Практикум по курсу "Информатика". Работас Windows, Word, Excel. Учебное пособие. – М.: Финансы и статистика, 2003. – 272 с.

3. ГлушаковС.В., Мельников И.В. Персональный компьютер. Учебное пособие. – Харьков: Фолио; М.: "АСТ", 2000. – 499 с.

4. ГлушаковС.В., СурядныйА.С. Персональный компьютер. – Харьков: изд-во "Фолио", 2005 г.

5. Гниденко И.Г., Соколовская С.А. Информатика. – СПб: изд-во "Дом "Нева", 2003. – 320 с.

6. ЖуринА.А. WindowsXP и Office 2003.Справочник пользователя ПК. Самоучитель. – М.:ООО «И.Д.Вильямс», 2007ю – 464 с.,:ил.

7. Информатика. Базовый курс / Под ред. С.В. Симоновича. – СПб.: Питер, 2000. – 640 с.

8. Информатика. Практикум по технологии работы на компьютере: учебное пособие / Под ред. Н.В. Макаровой. – М.: Финансы и статистика, 2000.

9. Информатика. Учебник / Под ред. Н.В. Макаровой. – М.: Финансы и статистика, 2000. – 767 с.

10. Леонтьев В.П. Новейшая энциклопедия персонального компьютера 2000. 2-е издание. – М.: Олма-пресс, 2000. – 847 с.

Навчальневидання

ЄфіменкоЛюбовСергіївна

Пантелєєва Ольга Гаврилівна

РуденськаВікторіяВолодимирівна

за дисциплінами «Економічна інформатика» та «Інформатика»

(ЧАСТИНА I)

Російськоюмовою

Підписано до друку 30.08.2012 р. Формат 60х84 1/16.

Ум.друк. арк. 3,5. Друклазерний. Зам. № 772. Тираж 150 прим.

Надруковано в ТОВ «Цифроватипографія»

Адреса: м. Донецьк, вул. Челюскінців, 291а, тел.: [phone]

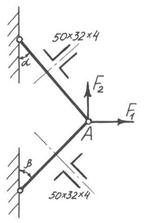
В заданій системі кожен стержень складається з двох нерівнобічних кутників 50×32×4. Допустима напруга для матеріалу стержнів [σ] =120 Н/мм².

Необхідно:

1) перевірити міцність стержнів та визначити відсоток пере- або недовантаження;

2) при необхідності змінити профіль перерізу.

Вихідні дані:

F₁ = 60 кН

F₂ = 40 кН

α = 30º

β = 40º

[σ] =120 Н/мм²

A₁ = A₂ = 2 A _∟= 2 · 3,17 см² =

=6,34 см² = 634 мм²

Розв’язок

1.1 Визначення внутрішніх нормальних сил в стержнях системи.

Звільняємо шарнір А від зв’язків (стержнів), замінюючи їх дію реакціями N₁ та N₂. Будуємо розрахункову схему задачі (рис. 1.1), обираємо осі координат та складаємо рівняння рівноваги:

Σ F_кx= 0: F₂cos 60º+ F₁cos 30º − N₂cos 20º = 0; (1.1)

Σ F_кy= 0: N₁ + F₂cos 30º− F₁cos 60º − N₂cos 70º = 0, (1.2)

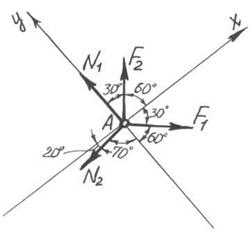
Рис. 1.1

Із рівняння (1.1) визначаємо N₂:

N₂ = 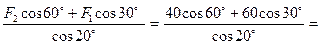76,58 кН

Із рівняння (1.2) визначаємо N₁:

N₁ = − F₂cos 30º+ F₁cos 60º + N₂cos 70º =

= − 40 cos 30º+ 60 cos 60º + 76,58 cos 70º = 21,55 кН

N₁ = 21,55 кН

N₂ = 76,58 кН

1.2 Перевірка міцності стержнів.

Перевірку міцності стержнів виконуємо за умовою міцності при розтязі-стисканні:

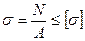, (1.3)

де σ – нормальна напруга в перерізі стержня, Н/мм²;

N – нормальна сила в перерізі, Н;

A – площа поперечного перерізу, мм²;

[ σ ] – допустима напруга, Н/мм².

1.2.1 Визначаємо напруги в поперечних перерізах стержнів

За формулою (1.5):

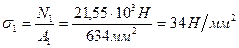
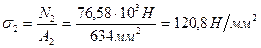
Стержень 1 недовантажений (σ₁ < [ σ ]);

Стержень 2 перевантажений (σ₂ > [ σ ]).

1.2.2 Обчислюємо відсоток недовантаження першого стержня та перевантаження другого стержня.

Δ₁ = 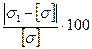% = % = 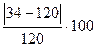71,7 %

Δ₂ = 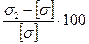% = % = 0,7 %

Недовантаження першого стержня перевищує допустимі 10 %, тобто він є неекономічним і для нього слід підібрати інший переріз.

Перевантаження другого стержня знаходиться в межах допустимих 5 %, тобто його змінювати не треба.

1.3 Підбір перерізу першого стержня.

Для першого стержня обираємо круглий переріз та визначаємо його діаметр.

1.3.1 За умовою міцності (1.5) виконуємо проектний розрахунок стержня

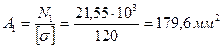
Для круглого перерізу 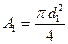, звідки визначаємо потрібний діаметр стержня:

d₁ =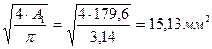

Округляємо діаметр до стандартного значення:

d_1ст =15 мм

1.3.2 Для прийнятого профілю з d_1ст =15 мм визначимо відсоток перевантаження:

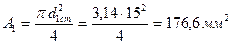
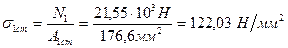
Δ _1ст = 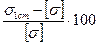% = % =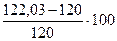1,7 % < 5 %.

Відповідь: перевірка міцності стержнів показала, що для першого стержня доцільно змінити профіль перерізу на круглий з діаметром d_1ст =15 мм, а для другого стержня переріз можна залишити незмінним – здвоєні нерівнобічні кутники 50×32×4.

2 Визначення головних центральних моментів інерції складного ПЕРЕРІЗУ

Для заданого складного перерізу визначити положення головних центральних осей та обчислити головні центральні моменти інерції.

Розв’язок

2.1. Визначення координат центру ваги перерізу.

2.1.1 Розбиваємо переріз на окремі прості частини та визначаємо їх площі:

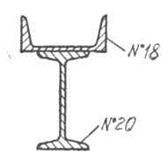
Ι – двотавр № 20

ІІ – швелер № 18

За даними таблиць сортаментів [3]:

А₁ = 26,8 см²

А₂ = 20,7 см²

2.1.2 Обираємо довільні осі координат x та y: вісь x проводимо по нижньому основанню двотавра, а вісь y суміщаємо з віссю симетрії перерізу (див. рис. 2.1)

2.1.3 Визначаємо координати центрів ваги окремих частин, користуючись даними таблиць сортаментів [3]:

x_c1= 0

x_c2= 0

y_c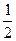1= h₁ = 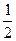∙ 20 = 10 см

y_c2= h₁+ z₀₂ = 20 + 1,94 = 21,94 см

2.1.4 Координати центру ваги складного перерізу визначаються за формулами:

x_c = 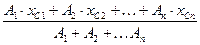; (2.1)

y_c = 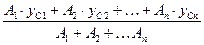, (2.2)

де А₁ , А₂ ,…, А_n – площі перерізів простих частин, см²;

x_c1 , x_c2 ,…, x_{c n} - координати центрів ваги простих частин по осі x, см;

y_c1 , y_c2 ,…, y_{c n} - координати центрів ваги простих частин по осі y, см.

Для заданого перерізу, який складається з 2-х простих частин:

x_c = 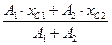= 0 см

y_c = 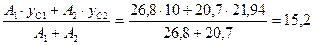см

2.2. Проведення власних центральних осей кожної частини та головних центральних осей всього перерізу.

Через центри ваги окремих частин проводимо їх власні центральні осі інерції: x₁, y₁; x₂, y₂ (див. рис. 2.1).

Так як переріз має вертикальну вісь симетрії, то головна центральна вісь Y співпадає з нею, а головну центральну вісь X проводимо через точку С перпендикулярно до осі Y (див. рис. 2.1).

Позначаємо на кресленні відстані між центральними осями кожної частини та головними центральними осями: a₁, a₂.

2.3. Визначення моментів інерції кожної частини відносно головної центральної осі X.

Момент інерції окремої простої частини відносно головної центральної осі X визначається за формулою:

I_X = I_x + a² ∙ A; (2.3)

де I_x – момент інерції окремої простої частини відносно власної центральної осі x, см⁴;

а – відстань між осями X та x, см;

А – площа перерізу, см².

Користуючись даними таблиць сортаментів [3] та формулою (2.3), визначаємо моменти інерції відносно головної центральної осі X для кожної частини:

a) для І частини:

I_X^І= I_x1^I+ a₁²∙A₁= 1840 + 5,2² ∙ 26,8 = 2564,7 см⁴

I_x1^I= 1840 см⁴

a₁ = y_c - y_c1 = 15,2 – 10 = 5,2 см

b) для ІІ частини:

I_X^ІІ= I_x2^ІІ+ a₂²∙A₂= 86 + 6,74² ∙ 20,7 = 1026,3 см⁴

I_x2^ІІ= 86 см⁴ (враховано нестандартне положення швелера в перерізі)

a₂ = y_c2 - y_c = 6,74 см

2.4. Визначення моментів інерції кожної частини відносно головної центральної осі Y.

Момент інерції окремої простої частини відносно головної центральної осі Y визначається за формулою:

I_Y = I_y+ b² ∙ A, (2.4)

де I_y - момент інерції окремої простої частини відносно власної центральної осі y, см⁴;

b - відстань між осями Y та y, см;

А – площа перерізу, см².

Користуючись даними таблиць сортаментів [3] та формулою (2.4), визначаємо моменти інерції відносно головної центральної осі Y для кожної частини:

a) для І частини:

I_Y^І= I_y1^I+ b₁²∙A₁= 115 см⁴

I_y1^I= 115 см⁴

b₁= 0 (так як осі Y та y₁ співпадають)

b) для ІІ частини:

I_Y^II= I_y2^II+ b₂²∙A₂= 1090 см⁴

I_y2^II= 1090 см⁴

b₂= 0 (так як осі Y та y₂ співпадають)

2.5. Визначення головних центральних моментів інерції перерізу .

Головні центральні моменти інерції складного перерізу визначаються за формулами:

I_X = I_X^І + I_X^ІІ + … + I_Xⁿ; (2.5)

I_Y = I_Y^І + I_Y^ІІ + … + I_Yⁿ , (2.6)

де I_X - момент інерції всього перерізу відносно осі X, см⁴;

I_Y - момент інерції всього перерізу відносно осі Y, см⁴;

I_X^І, I_X^ІІ,…, I_Xⁿ - моменти інерції складових частин відносно осі X, см⁴;

I_Y^І, I_Y^ІІ, …, I_Yⁿ - моменти інерції складових частин відносно осі Y, см⁴.

Для заданого перерізу, який складається з 2-х простих частин:

I_X = I_X^І + I_X^ІІ

I_Y = I_Y^І + I_Y^ІІ

Користуючись результатами обчислень п. 2.3 та п. 2.4, знаходимо:

I_X = 2564,7 + 1026,3 = 3591 см⁴

I_Y = 115 + 1090 = 1205 см⁴

Відповідь: Головні центральні моменти інерції складного перерізу мають значення: I_X = 3591 см⁴, I_Y = 1205 см⁴, тобто вісь X є віссю максимум, а вісь Y - віссю мінімум.

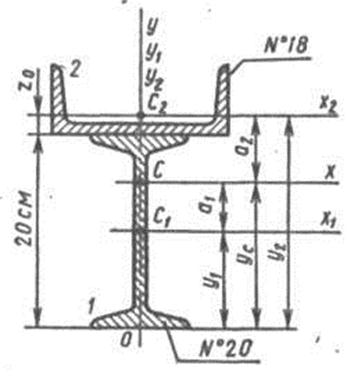
Рис. 2.1

3 Проектний розрахунок вала на кручення за умовою міцності

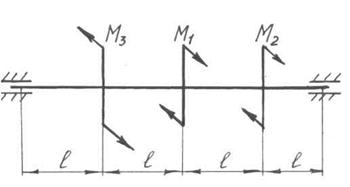
Сталевий вал постійного за довжиною перерізу навантажено зовнішніми скручуючи ми моментами М₁, М₂, М₃.

Допустима напруга при крученні для матеріалу вала [ τ ] = 30 Н/мм²; модуль зсуву G = 8∙10⁴ Н/мм²; довжина кожної ділянки навантаження l - 0,5 м.

Необхідно:

1) обчислити значення моментів М₁, М₂, М₃;

2) побудувати епюру моментів кручення М_к ;

3) з умови міцності визначити діаметри суцільного та кільцевого перерізів вала (для кільцевого перерізу прийняти співвідношення c = d /D = 0,7).

4) З умови жорсткості визначити діаметри суцільного та кільцевого перерізів вала (c = d /D = 0,7);

5) побудувати епюри кутів закручування для валів з прийнятими розмірами перерізів;

6) визначити економічність вала кільцевого перерізу відносно суцільного.

Вихідні дані:

P₁ = 52 кВт

P₂ = 50 кВт

ω = 20 рад/с

[τ] =30 Н/мм²

G = 8∙10⁴ Н/мм²

Розв’язок

3.1. Визначення обертальних моментів М₁, М₂, М₃.

Обертальні моменти на валу визначаються за формулою:

M = , (3.1)

де P – потужність, Вт;

ω – кутова швидкість вала, рад/с.

M₁ = 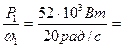2600 Н∙м

M₂ = 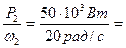2500 Н∙м

Момент M₃ знаходимо з рівняння рівноваги вала:

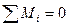; М₃ - М₁ - М₂ = 0

М₃ = М₁+ М₂= 2600+2500 = 5100 Н∙м

3.2. Побудова епюри моментів кручення M_к.

3.2.1. Визначаємо моменти кручення на окремих ділянках.

M_к^І= 0

M_к^ІІ= - М₂= - 2500 Н∙м

M_к^ІІІ= - М₂ – М₁ = - 2500 – 2600 = -5100 Н∙м

M_к^ІV= - М₂ – М₁+М₃= - 2500 – 2600 + 5100 = 0

3.2.2. За результатами розрахунків п. 3.2.1 будуємо епюру моментів кручення (див. рис. 3.1, б).

3.2.3. Визначаємо найбільш небезпечну ділянку та крутячий момент на ній.

Найбільш небезпечною є ІІІ ділянка;

M_{к max}= | M_к^ІІІ | = 5100 Н∙м

3.3. Визначення діаметру вала суцільного перерізу.

Умова міцності при крученні має вигляд:

τ_max = 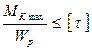, (3.2)

де τ_max – максимальна дотична напруга в небезпечному перерізі, Н/мм²;

M_{к max} – максимальне значення крутячого моменту, Н∙мм;

W_p – полярний момент опору перерізу, мм³;

[ τ ] – допустима напруга при крученні, Н/мм².

За мовою міцності (3.2) виконуємо проектний розрахунок вала.

Визначаємо потрібний полярний момент опору перерізу вала:

W_p ≥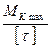

W_p ≥ 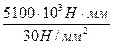= 170∙10³ мм³

Для суцільного кругового перерізу полярний момент опору визначається за формулою: W_p = 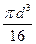[1], звідки:

d = = 95,2 мм

Приймаємо стандартне значення діаметру:

d_суц= 95 мм

3.4. Визначення діаметрів вала кільцевого перерізу.

Для кільцевого перерізу полярний момент опору визначається за формулою: W_p = 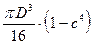[1], звідки зовнішній діаметр кільця:

D = 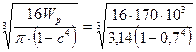= 104,5 мм

Внутрішній діаметр кільця:

d = c ∙D = 0,7 ∙ 104,5 = 73,15 мм

Приймаємо стандартні значення діаметрів:

D_кільц= 105 мм

d_кільц= 74 мм

3.5. Визначення кутів закручування вала суцільного перерізу з прийнятим діаметром d_суц= 95 мм.

Для суцільного перерізу з прийнятим діаметром d_суц= 95 мм визначимо полярний момент інерції:

I_p= 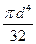= = 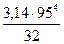7992343 мм⁴

Кут закручування окремої ділянки з постійним моментом кручення на ній можна визначити за формулою:

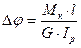, (3.3)

де М_к – крутячий момент на ділянці, Н∙мм;

l – довжина ділянки, мм;

G – модуль зсуву, Н/мм²;

I_p – полярний момент інерції перерізу, мм⁴.

За формулою (3.3) визначаємо кути закручування окремих ділянок вала:

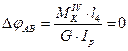
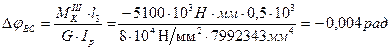
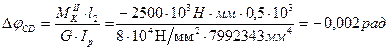
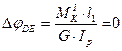
3.6 Побудова епюри кутів закручування вала суцільного перерізу.

Для побудови епюри кутів закручування вала переріз А умовно приймаємо за нерухомий, а значення кутів повороту окремих перерізів обчислюємо відносно нього:

φ_А= 0

φ_В= Δ φ_АВ= 0

φ_С= φ_В + Δ φ_ВС = 0 – 0,004 = -0,004 рад

φ_D= φ_С + Δ φ_СD= - 0,004 – 0,002 = - 0,006 рад

φ_E= φ_D+ Δ φ_DE= - 0,006 + 0 = 0,006 рад

За результатами обчислень будуємо епюру φ_суц (див. рис. 3.1,в).

3.7 Визначення кутів закручування вала кільцевого перерізу з прийнятими діаметрами D_кільц = 105 мм; d_кільц= 74 мм.

Для кільцевого перерізу з прийнятими діаметрами визначимо полярний момент інерції:

I_p= 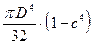= = 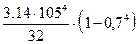9063445 мм⁴

Користуючись формулою (3.3) визначаємо кути закручування окремих ділянок вала:

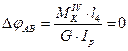
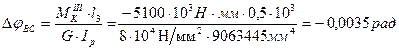
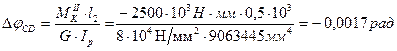
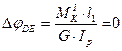
3.8 Побудова епюри кутів закручування вала кільцевого перерізу.

φ_А= 0

φ_В= Δ φ_АВ= 0

φ_С= φ_В + Δ φ_ВС = 0 – 0,0035 = -0,0035 рад

φ_D= φ_С + Δ φ_СD= - 0,0035 – 0,0017 = - 0,0052 рад

φ_E= φ_D+ Δ φ_DE= - 0,0052 + 0 = - 0,0052 рад

За результатами обчислень будуємо епюру φ_кільц (див. рис. 3.1,г).

3.9 Визначення економічності вала кільцевого перерізу по відношенню до суцільного.

Маси валів відносяться як площі їх поперечних перерізів, тобто:

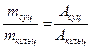
А_суц=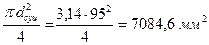

А_кільц=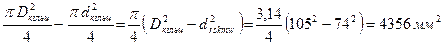

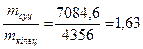
Відповідь: вал кільцевого перерізу за витратою матеріалу є економічнішим, ніж вал суцільного перерізу в 1,63 рази;при цьому характеристики жорсткості відрізняються несуттєво.

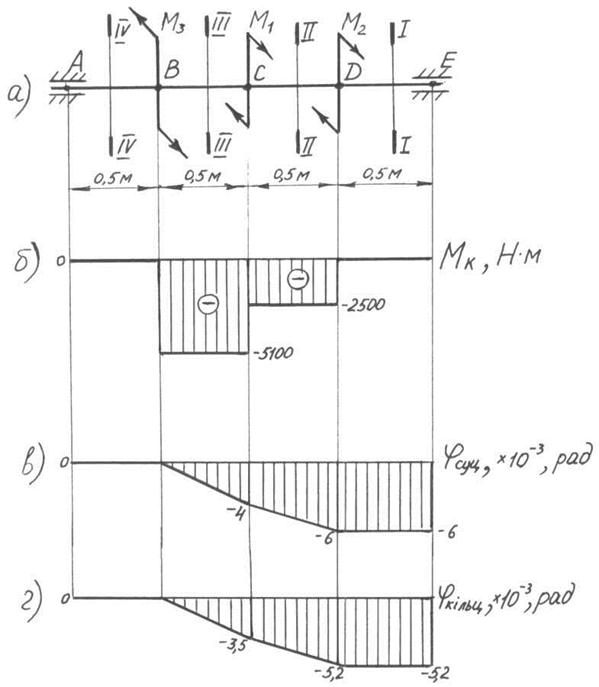
Рис. 3.1

4 РОЗРАХУНОК БАЛКИ ПРИ ПЛОСКОМУ ПОПЕРЕЧНОМУ ЗГИНІ

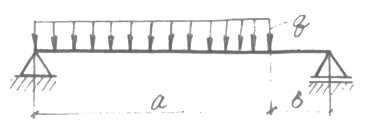
Для двохопорної балки, навантаженої згідно схеми, необхідно:

6) визначити реакції опор;

7) скласти рівняння поперечних сил та згинаючих моментів для кожної ділянки балки;

8) побудувати епюри поперечних сил та згинаючих моментів

9) визначити найбільш небезпечний переріз балки та максимальний згинаючий момент;

10) підібрати найбільш економічний переріз балки з 4-х можливих варіантів: круг, квадрат, прямокутник (h=2b), двотавр.

Допустима напруга згину матеріалу балки [ σ ] = 160 Н/мм².

Вихідні дані:

q= 10 кН/м

a= 4 м

b= 1 м

[σ] = 160 Н/мм²

Розв’язок

4.1 Визначення реакцій опор балки.

Будуємо розрахункову схему балки (рис. 4.1, а) та визначаємо рівнодіючу розподіленого навантаження:

Q = q∙l = 10∙4 = 40 кН/м

Складаємо рівняння рівноваги та визначаємо реакції опор балки:

Σ М_А= 0: R_B∙(4 + 1) – Q ∙2 = 0; (4.1)

Σ М_B= 0: - R_A∙(4 + 1) + Q∙(1+2) = 0. (4.2)

Із рівняння (4.1):

R_B= 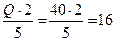кН

Із рівняння (4.2):

R_A = 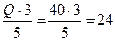кН

Для перевірки знайдених реакцій складаємо додаткове рівняння рівноваги:

Σ F_кy= 0: R_A – Q + R_B= 0

24 – 40 + 16 = 0

0 = 0

Перевірка підтвердила вірність знайдених значень R_A і R_B.

4.2 Складання рівнянь поперечних сил та згинаючих моментів для кожної з ділянок балки.

Розбиваємо балку на окремі ділянки та визначаємо поперечні сили Q_y та згинаючі моменти M_x на них.

І ділянка

0 ≤ z ≤ 4 м

Q_y^I = R_A∙ - q∙ z = 24 – 10∙z

При z = 0: Q_y^I = 24 – 0 = 24 кН

При z = 4: Q_y^I = 24 – 10 ∙ 4 = - 16 кН

M_x^І = R_A∙ z - q∙ z²/2

При z = 0: M_x^І = 0

При z = 4 м: M_x^І = 24 ∙ 4 - 10∙ 4²/2 = 16 кН∙м

Епюра Q_y перетинає нульову лінію, отже в цій точці епюра моментів має екстремум. Визначаємо координату z₀ точки екстремума:

Q_y^I = 24 – 10∙z₀ = 0

z₀ = 24/10 = 2,4 м

При z = 2,4 м: M_x^І = 24 ∙ 2,4 - 10∙ 2,4²/2 = 28,8 кН∙м

ІІ ділянка

4 м ≤ z ≤ 5 м

Q_y^IІ = R_A∙ - q∙ 4 = 24 – 10∙4 = - 16 кН∙

M_x^ІІ = R_A∙ z - q∙ 4 (z – 2) = 24∙ z - 40∙(z – 2)

При z = 4 м: M_x^ІІ = 24∙ 4 – 40 (4 – 2) = 16 кН∙м

При z = 5 м: M_x^ІІ = 24∙ 5 – 40 (5 – 2) = 0 кН∙м

4.3 Побудова епюр поперечних сил та згинаючих моментів.

За результатами розрахунків п. 4.2 будуємо епюри поперечних сил Q_y та згинаючих моментів M_x (рис. 4.1 б, в).

4.4 Визначення найбільш небезпечного перерізу максимального згинаючого моменту.

За епюрою M_x визначаємо, що найбільш небезпечний переріз знаходиться в точці С на перший ділянці, оскільки тут згинаючий момент приймає максимальне значення:

M_{x max}= 28,8 кН∙м

4.5 Підбір перерізів балки.

Умова міцності при згині має вигляд:

σ_max= 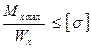, (4.3)

де σ_max – максимальна нормальна напруга в небезпечному перерізі, Н/мм²;

M_{x max} - згинаючий момент в небезпечному перерізі, Н∙мм;

W_x – осьовий момент опору, мм³;

[ σ ] – допустиме значення нормальної напруги, Н/мм².

Користуючись формулою (4.3), визначаємо потрібний осьовий момент опору перерізу балки:

W_x ≥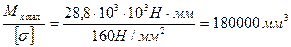

Підберемо перерізи з найближчим більшим значенням W_x.

4.5.1 Підбір круглого перерізу

Для круглого перерізу осьовий момент опору визначається за формулою: W_x= 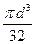[2], звідси:

d = 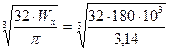= 122,4 мм

Приймаємо стандартне значення діаметру d_1ст = 124 мм

4.5.2 Підбір квадратного перерізу

Для квадратного перерізу осьовий момент опору визначається за формулою: W_x= 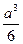[2], звідси:

a =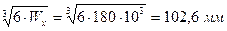

Приймаємо стандартне значення a_ст = 104 мм

4.5.3 Підбір прямокутного перерізу

Для прямокутного перерізу осьовий момент опору визначається за формулою: W_x= 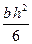[2]. Враховуючи, що за умовою h=2b, отримаємо: W_x= 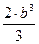, звідси:

b=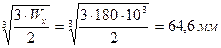

h=2b = 2∙64,6 = 129,2 мм

Приймаємо стандартні значення:

b_ст = 65 мм

h_ст = 130 мм

4.5.4 Підбір двотаврового перерізу

Користуючись таблицею сортаментів [3], підбираємо двотавр № 20 з осьовим моментом опору W_x = 184 см³ = 184000 мм³.

4.6 Визначення найбільш економічного перерізу.

Найбільш економічний переріз знаходимо порівнянням площ підібраних перерізів

- для круглого перерізу:

A= ;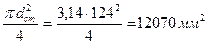

- для квадратного перерізу:

А= а²= 104² = 10816 мм²;

- для прямокутного перерізу:

А= h_ст∙ b_ст = 130∙ 65 =8450 мм²;

- для двотаврового перерізу:

А= 26,8 см² = 2680 мм².

Найбільш економічний переріз – двотавр № 20 з А= 26,8 см² = 2680 мм².

Відповідь: для балки, що зазнає плоский поперечний згин в вертикальній площині, найбільш доцільно використовувати двотавровий переріз із стандартним розташуванням.

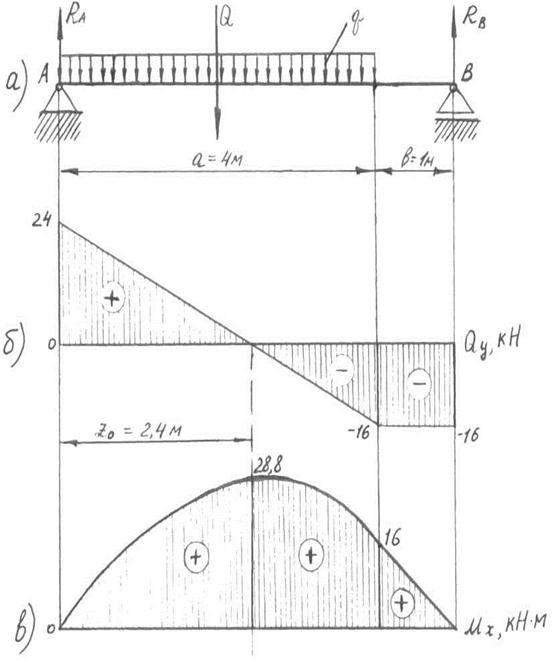
Рис.4.1

ПЕРЕЛІК ПОСИЛАНЬ

1. Аркуша А. И.. Техническая механика. Теоретическая механика и сопротивление материалов. – М.: Высш. шк., 2002.

2. Ицкович Г. М. Сопротивление материалов.- М.: Высш. шк., 2000.

3. Ицкович Г. М., Винокуров А. И., Барановский Н. В. Сборник задач по сопротивлению материалов. – Л.: Судостроение, 1972.

Дата добавления: 2014-11-18