Моделирование

Под моделированием понимается изу­чение экологических процессов с по­мощью лабораторных, натурных или математических моделей. Модели биосистем столь многочисленны, что классификация их почти невозможна.

Модель - это имитация того или иного явления реаль­ного мира, позволяющая делать прогнозы.

В простейшей форме модель может быть вербальной (словес­ной) или графической, т. е. неформализованной. Если необхо­димы достаточно надежные количественные прогнозы, то модель должна быть формализованной, строго математической. Моде­ли, созданные на ЭВМ, позволяют получать на выходе искомые характеристики при изменении, добавлении или исключении каких-либо параметров модели, т.е. возможна «настройка» математи­ческой модели, позволяющая усовершенствовать ее, приближая к реальному явлению.

На протяжении XIX и первой половины XX веков применение математики для отслеживания природных явлений было уделом талантливых одиночек. Сейчас использование математических методов не только для обработки экспериментов, но и для описания работы биосистем становится массовым.

Толчок развитию моделирования, как в биологии вообще, так и в экологии в частности, дала кибернетика. Но относиться к математическому описанию работы биосистем нужно с осторож­ностью, и прежде всего необходимо доказать адекватность ис­пользуемого математического аппарата объекту и целям иссле­дования.

Создание методологии и технологии моделирования биосистем, а тем более самых сложных из них - экосистем, - дело будущего. Можно лишь наметить некоторые этапы в развитии технологии моделирования: 1) переход от эксперимента к адекватной матема­тической модели; 2) построение математических моделей с различ­ной глубиной содержания; 3) переход от одних моделей к другим; 4) систематизация математических моделей биосистем различных иерархических уровней. Но, несмотря на необходимость крити­ческого взгляда на математическое моделирование явлений приро­ды, назад, к чисто описательной экологии, дороги нет.

Стратегия моделирования заключается в попытке путем упро­щения получить модель, свойства и поведение которой можно легко изучать. В то же время модель должна иметь достаточное сходство с оригиналом. Переход от модели к оригиналу называется интер­претацией модели. Обычно оригинал представляет собой много­компонентную систему, где взаимодействия между популяциями столь сложны, что не поддаются достаточно удовлетворительному анализу. В то же время законы функционирования некоторой модели могут быть найдены тем или иным путем. Учитывая это, исследование системы можно заменить исследованием модели, а затем интерпретировать результаты применительно к оригиналу.

В.Д. Федоров и Т.Г. Гильманов (1980) предлагают следующую классификацию моделей, используемых в экологии (рис. 7.3).

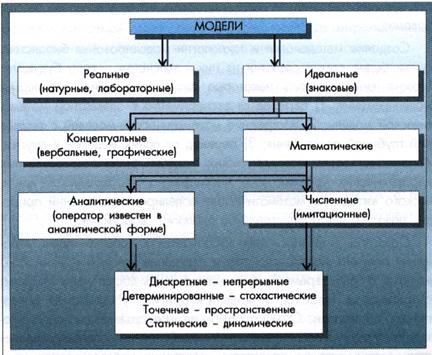
Наиболее сложная проблема при работе с реальными лабораторными моделями - установление адекватности модели оригиналу, а следовательно, обоснование возможности применения результатов моделирования к изучаемой природной системе. В отличие от аэро- или гидродинамики, где разработаны количественные критерии подобия модели оригиналу (критерий Рейнольдса и др.), в экологии таких критериев нет. Возможности идеальных знаковых моделей богаче, чем реальных, так как их создание почти не имеет технических ограничений.

Рис. 7.3. Схема классификации моделей (по В.Д. Федорову и Т.Г. Гильманову, 1980, с изменениями)

Знаковые модели - концептуальные и математические - имеют в экологии большое значение.

Концептуальная модель представляет собой более или менее формализованный вариант традиционного описания изучаемой экосистемы, состоящего из текста, блок-схемы, таблиц, графиков.

В итоговых публикациях Международной биологической прог­раммы 1964 - 1974 гг. представлены концептуальные модели важнейших типов экосистем, обеспеченные количественными дан­ными о динамике численности и биомассы популяций и т.п.

Концептуальные модели, наряду со многими достоинствами (универ­сальность, гибкость и др.), имеют и недостатки: неоднозначность интерпретации и статичность. Наиболее известно моделирование Великих озер в США (рис. 7.4).

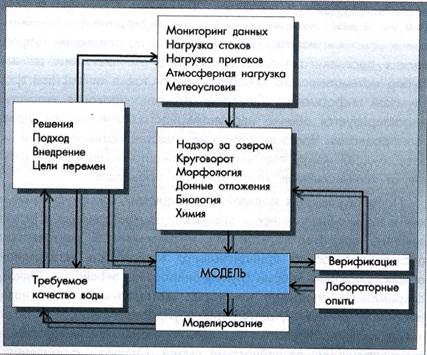Рис. 7.4. Процесс моделирования управления качеством воды на Великих озерах (по У. Ричардсону, 1979)

Методы математического моделирования при изучении экосистем в динамике более эффективны. При конструировании математических моделей экосистем прослеживаются две тенден­ции. Математики часто берутся за глубокую теоретическую разработку моделей, неадекватность которых известна заранее. А экспериментаторы и натуралисты пытаются включить в модель как можно большее число изученных свойств моделируемого объекта, не заботясь об их значимости. При этом, если реаль­ные процессы неверно оцениваются количественно, то модель, естественно, даст неправильную картину экосистемы в целом. Математические модели могут быть классифицированы по ряду признаков, в соответствии с которыми выбирается аппарат какого-либо раздела математики, призванный служить языком описания свойств, структуры и поведения оригинала. Различают априорные (лат. a priori - независимо от опыта) и апостериорные (лат. a posteriori - основанные на опыте) модели. Первые выводятся на основании теоретических посылок, а вторые строятся по эмпирическим данным. Выбор математического аппарата зависит также от состава фактической информации. Описание функционирования экосистем характеризуется обычно неравномерностью изученности отдельных процессов. Часто не только не известен математический вид зависимостей между отдельными компонентами, но вообще отсутствуют количественные характеристики процессов.

Попытки создания моделей, совмещающих физико-динамические и химико-биологические процессы, обычно приводят к исполь­зованию дифференциальных уравнений. К достоинствам последних относится принципиальная возможность установления общих положений теории функционирования экосистем. Однако современное состояние некоторых математических дисциплин (теории устойчивости, оптимального управления и др.) не позво­ляет достаточно подробно исследовать системы высокого порядка с существенными нелинейностями связей. Отсюда - стремление к применению обобщенных компонентов и характеристик для снижения порядка системы.

Возможность получения картины общих закономерностей жизни экосистем на основании аналитического исследования даже простых теоретических моделей была показана многими авторами. Рассмотрим для примера простую классическую модель роста биомассы микроскопических водорослей в водоеме (фитопланктона) - модель Флеминга (1939). Изменение био­массы в данной модели определяется двумя процессами: цветением водорослей и выеданием их микроскопическими животными (зоопланктоном).

Модель записывается в виде дифференциального уравнения

д P/д t = P[a-(b+ct)], (7.1)
где Р - биомасса фитопланктона в столбе воды над единицей площади; а – удельная скорость роста биомассы фитопланктона; с – постоянный коэффициент увеличения скорости выделения фитопланктона зоопланктоном; (b+сt) – коэффициент выедания, зависящий от времени t.

Численные значения коэффициентов уравнения были получе­ны по материалам натурных исследований в Английском канале. Частное решение уравнения имеет вид

P_t = P₀exp[(a-b)t-0,5ct2], (7.2)
где Р_t, Р₀ - биомасса в момент времени t, t₀.

В период цветения изменение биомассы водорослей эквива­лентно увеличению биомассы зоопланктона. Это подчеркивается введением понятия «доля фитопланктона, выедаемая за сутки» - DР. Зависимость DР от количества зоопланктона N_t и его филь­трационной способности V(л/сут) записывается в виде

DР = N_t + VPDt. (7.3)
Сравнивая выражения (7.3) и (7.1), получаем

N_t V = b + сt. (7.4)

Общая биомасса фитопланктона С_t за промежуток времени от t₀ до t может быть рассчитана по формуле

t

С_t = aP₀ òexp[(а-b)t-0,5ct²]д t (7.5)
t₀

Работа Флеминга является одной из первых попыток математи­ческого моделирования сезонного хода важнейшей составляющей экосистемы моря - фитопланктона. Эти приемы широко использовались в последующих исследованиях.

С учетом условности отображения в модели реальных параметров построение математической модели биосистемы можно выполнять параллельно с исследованием в натуре или с постанов­кой экспериментов. При этом поиск наилучшей структуры мо­дели можно производить автоматически на ЭВМ на основании некоторой системы критериев. В то же время полная автоматизация не всегда эффективна. В некоторых случаях целесообразно поручить человеку осуществлять выбор типа, структуры модели и критериев наилучшего сходства модели и оригинала (рис. 7.5).

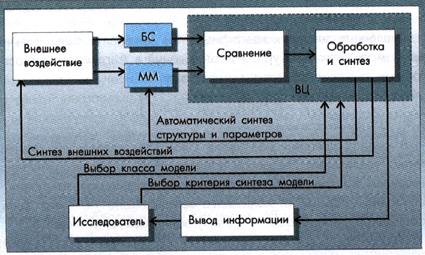Рис. 7.5. Автоматическая система моделирования; БС - биосистема; ММ -математическая модель; ВЦ - вычислительный центр

При моделировании экологических систем на основе дифференциальных уравнений не следует забывать о фундаментальных экологических принципах и прежде всего о принципе эмерджентности, т.е. о том, что экосистема обладает качественно новыми свойствами, которые нельзя предсказать исходя из свойств отдельных ее компонентов. Поэтому информационная база, состоящая из множества отдельных физических, химических и биологических показателей, не может в полной мере отразить законы функционирования природного объекта. Необходимо учитывать и то, что экосистемы управляются и контролируются не всеми, а ключевыми, эмерджентными факторами. Поэтому многие специалисты, и классик американской школы экологов Ю. Одум в том числе, утверждают: «для построения удовлетворительных математических моделей не требуется необъятного количества информации об огромном множестве переменных». Кроме того, стремление приблизиться к оригиналу с помощью наращивания показателей входит в противоречие с оперативностью решения задач. Таким образом, практическая реализация «экологических» моделей природных комплексов еще не достигла значительных успехов.

Создание работоспособной модели многокомпонентной системы, функционирующей в трехмерном пространстве и во времени, связано с решением многих проблем, основными из которых являются следующие:

1. Выбор функциональных зависимостей и параметров, описывающих процессы обмена веществом и энергией между физическими и химико-биологическими компонентами. Сложность проблемы усугубляется тем, что многие процессы: турбулентность, гравитация, кинетика реакций, взаимоотношения организмов и т.п. - еще далеко не полностью изучены.

2. Информационный «голод» на начальном этапе моделирования, т.е. отсутствие, как правило, трехмерных полей синхронных наблюдений физических, химических и биологических характеристик, изменяющихся во времени. Иначе говоря, возникает несоответствие между желаниями исследователя и техническими возможностями при ограниченном объеме фактической информации. Операции заданий входной и анализа выходной информации вырастают в самостоятельные проблемы.

3. Реализация алгоритма моделирования экосистемы. Это связано с разработкой целого комплекса взаимосвязанных программ для описания весьма сложных физических и химико-биологических процессов. Решение каждой из задач в отдельности представляет собой самостоятельную проблему, требующую огромной работы. Далее возникает проблема информационной и программной увязки отдельных подсистем. Комплекс задач моделирования экосистемы в цепом перерастает, по существу, в автоматизированную систему анализа поведения избранного объекта, а процесс создания «экологической» модели становится соизмеримым с процессом создания автоматизированных систем управления.

Статистические модели, по мнению многих авторов, работавших в области моделирования биосистем, являются более прагматичными. Действительно, взаимосвязи между компонентами экосистемы можно формально описать методами математической статистики, т.е. на основе натурных данных. Множественный корреляционный или регрессионный анализы полезны как для установления факта зависимости между отдельными элементами системы, так и для получения уравнений регрессии, которые могут служить моделями экосистемы или отдельных подсистем. Однако возможности прогнозирования временной динамики ограничены условиями, в которых получена исходная информация.

В качестве примера рассмотрим регрессионную модель эпидемических процессов. На возникновение, развитие и распространение эпидемии влияют самые различные факторы окружающей среды в том или ином районе. Например, предварительное изучение заболеваний дизентерией (за 20 лет в одном из районов России) выявило из двадцати факторов пять, оказывающих наибольшее влияние на эпидемию: температура воздуха (х₁), атмосферные осадки (х₂), атмосферное давление (х₃), влажность воздуха (х₄), активность солнца (х₅). Количествен­ные значения этих факторов по месяцам в течение 20 лет составили банк исходных данных для построения математичес­кой модели. Выходной величиной, т.е. критерием степени рас­пространения эпидемии, являлось число заболевших (y).

Задача состояла в построении математической модели, связываю­щей число заболевших с числовыми значениями метеофакторов. Если определять возможное среднее число заболеваний в год, то для построения модели следует привлекать среднегодовые значе­ния факторов. Можно строить модель и относительно числа забо­леваний на данный месяц. Можно считать также, что коэффициенты модели сами являются функциями времени, зависящими от месяца, но в этом случае модель усложняется. Зависимость числа заболеваний от пяти наиболее значимых факторов запишем в виде линейной функции

у = а₁х₁ + а₂х₂ + а₃х₃ +а₄х₄ + а₅х₅ (7.6)

Для определения коэффициентов уравнения регрессии мето­дом наименьших квадратов используется массив исходных дан­ных (заболеваемость и значения метеофакторов). В данном при­мере получено уравнение

у = 0,178х₁ + 0,175х₂ - 0,359х₃ - 0,294х₄ - 0,164х₅. (7.7)

Коэффициенты уравнения перед входными величинами (х₁, …, х₅) одновременно со служебной ролью определяют и степень влияния каждого фактора на выходную величину. Для уравнения (7.7) вычисляют коэффициент множественной корреляции R₁ = 0,416 и дисперсию s₁² = 1,001.

Регрессионные модели не ограничиваются линейной формой. В процессе поиска можно перейти к более сложной модели - уравнению нелинейной регрессии:

y =°a₁x₁ + а₂x₂ +°а₃x₃ +°a₄x₄ +°a₅x₅ +a₆x₁² + a₇x₂² + a₈x₃² +a₉x₄² + a₁₀x₅². (7.8)

На основании того же массива исходного материала можно рассчитать значения коэффициентов множественной корреляции и дисперсии для уравнения (7.8):

R₂ = 0,659; s₂² = 0,684.

При переходе к нелинейной модели коэффициент корреля­ции увеличился, а дисперсия экспериментальных данных уменьши­лась. Это означает, что последняя модель более точна, чем линейная функция. Однако при последующем усложнении моде­ли в виде полинома третьей степени коэффициент множествен­ной регрессии R₃ = 0,648 уменьшился, а дисперсия s₃² = 0,695 увеличилась. Следовательно, точность математического описания при переходе к полиному третьей степени ухудшилась. Поэтому в данном случае целесообразно в качестве адекватной использо­вать квадратичную регрессионную модель (7.8).

На основании информационного массива данных по месяцам можно построить математическую модель, отражающую динамику изменения числа заболеваний в течение года в зависимости от метеофакторов. Для этого в модели, выбранной в качестве оптимальной (7.8), за шаг времени нужно взять месяц, а каждый коэффициент уравнения представить в виде некоторой функции времени а_i = f(t), i = 1, 2,...., 10.

Но «никакие, даже самые совершенные модели экологических систем не могут развиваться или паже просто поддерживаться без постоянной корректировки, используя результаты натурных наблюдений», - пишет В.В. Меншуткин (1995). В живой природе жизнь организмов определяется разнообразными факторами внутреннего и внешнего порядка.

При изучении качественных или количественных характеристик организма, популяции или сообщества практически никогда не наблюдают одинаковые значения даже для одной особи, а получают ряд несовпадающих чисел. Каждое из них, на первый взгляд, может казаться истинным. Поэтому характеристику изучаемого свойства следует давать не по разовым измерениям, а по всей совокупности полученных результатов. Однако иметь дело с таким множеством данных неудобно, поэтому желательно «уплотнить» информацию.

При любом моделировании предварительно следует проводить статистическую обработку исходных натурных или экспериментальных данных с целью преобразовании, их в немногие параметры, которые в компактной форме достаточно полно характеризуют свойства экосистемы.

Другая задача математической статистики в экологии связана с тем, что исследователь почти никогда не имеет возможности изучить все компоненты экосистемы. Обычно изучается лишь не­кая выборка. В связи с этим возникает проблема оценки степени соответствия свойств выборки свойствам всей совокупности. Отве­ты на эти вопросы также дает математическая статистика. Наиболее важным является использование статистики для изучения характера связей между отдельными функциями живого орга­низма, между разными организмами, между организмами и факторами неживой среды.

Разумеется, область применения статистических методов значи­тельно шире, а разнообразие методов очень велико. Экологам необходимо помнить, что пренебрежение статистической обра­боткой исходной информации при построении математических моделей может приводить к дискредитации самой модели.

Наряду со статистическим анализом для уплотнения информа­ции, ведутся усиленные поиски репрезентативных интегральных критериев для оценки эмерджентных свойств экосистем. Это может стать началом нового этапа системных наблюдений при­родных явлений.

Схема системного исследования

Общая схема системного - исследования предложена В.Д. Федоровым и Т.Г. Гильмановым (1980). Все рас­смотренные выше методы (наблюдение, эксперимент, моделирование) объединяются в единый процесс экологического исследова­ния, который должен осуществляться в рамках междисциплинарного исследовательского проекта.

Процесс системного исследования целесообразно разделить на ряд этапов, выполняемых последовательно или параллельно (рис. 7.6).

Постановка задачи и концептуализация. При реше­нии той или иной экологической проблемы (охрана природы, рациональное использование ресурсов, управление, прогноз эко­логического состояния и др.) можно выделить ограниченное и достаточное число наиболее существенных факторов, свойств или процессов. Назначение первого этапа состоит в выборе наиболее важных приоритетных задач, определяющих направление дальнейших исследований.

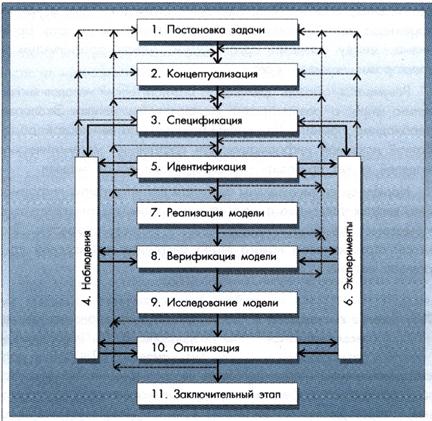
Рис. 7.6. Общая схема системного изучения экосистемы (по В.Д. Федотову, Т.Г. Гильманову, 1980)

Задача концептуализации состоит в том, чтобы суммировать известную информацию об изучаемой экосистеме в виде логичес­ки непротиворечивой концептуальной модели. Модель концентри­рует данные, необходимые для решения рассматриваемой пробле­мы. Определяется место изучаемой экосистемы в ландшафте, устанав­ливаются ее «входы» и «выходы», т.е. связи с соседними экосистемами, атмосферой, гидросферой, твердой средой, деятельностью человека и т.п. (рис. 7.7). Далее в модели характеризуются состав, структура и главные особенности санкционирования экосис­темы, т.е. определяются число компонентов и совокупность связей.

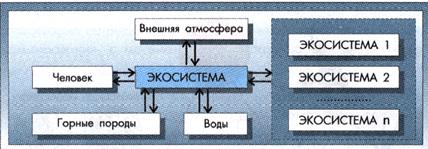Рис. 7.7. Концептуальная модель внешних связей экосистемы (по В.Д. Федотову, Т.Г. Гильманову, 1980)

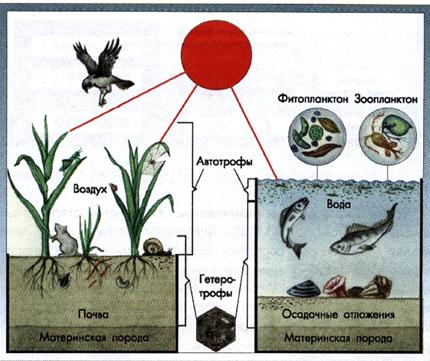
Спецификация и наблюдения. Назначение этапа специ­фикации состоит в том, чтобы определить состав входных пере­менных, переменных состояния экосистемы и, по возможности, строго задать отображение оригинала на модель. При специфика­ции указывается, с какими измеряемыми характеристиками экосис­темы и внешней среды сопоставляются переменные ее состояния, какие методы и единицы измерения используются. При этом целесооб­разно создавать автоматизированные компьютерные банки дан­ных. Принципиальная схема состава и структуры наземной и водной экосистем показана на рис. 7.8.

На основании спецификации и концептуальной модели плани­руются полевые наблюдения за динамикой изучаемых свойств экосистемы и прежде всего за переменными экологического сос­тояния и входными характеристиками. Результаты наблюдений используются на последующих этапах работы (идентификация, проверка и исследование модели). Кроме того, они могут служить основой для пересмотра в случае необходимости концептуальной модели, что показано на рис. 7.6 линией от блока 4 к блоку 2.

Идентификация и эксперименты. Задача идентифика­ции заключается в математическом описании соотношений между переменными, образующими структуру модели. В частности, основу структуры динамических моделей с n переменными состояния состав­ляют чаще всего n дифференциальных уравнений, выражающих закономерности изменения каждой из переменных во времени.

Рис. 7.8. Схема состава и структуры наземной и водной экосистем

При идентификации, как правило, возникает потребность в проведении полевых или лабораторных экспериментов с целью проверки различных гипотез о характере взаимосвязей между компонентами экосистемы или для оценок параметров известных зависимостей. Экспериментальные работы проводятся параллельно с другими стадиями исследования, вследствие чего возможно возвращение к предыдущим этапам и их повторение в новом цикле исследований с учетом дополнительной информации, полученной в результате эксперимента.

Реализация и верификация модели. После идентификации модели встает проблема ее реализации, т.е. нахожде­ния оператора, который позволит рассчитывать динамику состо­яния экосистемы во времени в соответствии с входными данны­ми и начальным состоянием. Обычно реализация осуществляется в виде программы расчета на ЭВМ. На этом этапе очень плодотворно сотрудничество экологов, владеющих основами программирования, с математиками, достаточно глубоко изучившими основы экологии.

Верификация модели (лат. verificatio - проверка подлинности) имеет целью проверить, в какой степени модель соответствует оригиналу. Оценка пригодности модели может быть дана на основе срав­нения с данными наблюдений и, главное, на основе опыта прак­тического использования модели как инструмента прогнозиро­вания, оптимизации и управления моделируемой системой. Од­нако предварительные сведения об адекватности модели необхо­димы в течение процесса ее построения.

Существует много способов оценки адекватности моделей. Р. Сайерт (1966) предложил, например, проверять способность модели воспроизводить такие характеристики эмпирических кривых, как число и распределение экстремальных точек во времени, амплитуда возмущений, средние значения переменных и др. Т.Г. Нейлор и Д. Фигнер (1975) предлагают производить сравнение статисти­ческих критериев модели и наблюдений: математического ожида­ния, дисперсий, асимметрий, эксцессов и др. Однако наиболее наглядным способом проверки модели является сравнение расчет­ных кривых ее состояния в рассматриваемом интервале времени с данными наблюдений за системой за тот же промежуток времени. Кривые могут быть построены по непрерывным или дискретным наблюдениям. Для оценки степени совпадения могут быть использо­ваны как численные значения характеристик, так и статистические показатели. При хорошем совпадении расчетных и эмпирических данных модель можно считать адекватной оригиналу и приступать к проверке других аспектов ее работы. Однако часто обнаружи­вается, что нет удовлетворительного совпадения результатов модели­рования с эмпирическими данными. В поисках причин приходится возвращаться к предшествующим этапам (чаще всего к этапу иден­тификации). После этого последовательность этапов повторяется до тех пор, пока не будет достигнуто требуемое согласие. Эффективным способом проверки модели являются также имитация на ней разнообразных экспериментальных воздействий (орошения, удобре­ния, изменения температуры, течений и т.п.) и сравнение получен­ных результатов с данными реальных экспериментов.

Неспособность модели правильно предсказать последствия тех или иных воздействий является основанием для ее пересмотра. Но абсолютно точного воссоздания оригинала требовать от модели нереалистично. Поэтому при достаточно надежной концептуаль­ной модели и хороших критериях адекватности после нескольких проверок и исправлений обычно удается построить приемлемую модель и приступить к дальнейшему исследованию.

Заключительный этап основывается на исследовании мо­дели и оптимизации решений. Процесс исследования включает описание общих черт изменения состояний и поведения модели в зависимости от изменения входных данных. Один из основных разделов исследования - анализ «чувствительности» модели. Резуль­таты этой операции показывают, какие начальные условия, взаимо­связи между переменными, внешние факторы или другие парамет­ры оказывают наиболее сильное (или, наоборот, незначительное) влияние на поведение модели. После получения ответов можно решить, какие параметры должны определяться с высокой точностью, а какие могут задаваться приближенно при наблюде­ниях, экспериментах и идентификации. Данные теоретических исследований модели и результаты имитационных расчетов дают дополнительную информацию для оценки адекватности модели и необходимости ее дальнейшего усовершенствования.

В практической работе по охране или рациональному исполь­зованию природных экосистем человек может задавать и регулиро­вать те или иные воздействия с целью оптимизации их состояния в нужном направлении. Например, при управлении заповедни­ком стремятся к сохранению редких видов организмов, в агроэкосистемах - к получению высокого урожая. При управлении водоемом можно использовать принудительную аэрацию для оптимизации его экологического состояния и т.п.

При многоцелевом использовании природных ресурсов при­ходится сталкиваться с противоречиями. Например, трудно совмес­тить забор питьевой воды с пляжем или сбросом в водоем сточных вод. Поэтому часто решение оптимизационных задач носит компромиссный характер, обусловленный многофактор­ностью и множеством критериев качества. Методической осно­вой решения таких задач являются теория оптимального управле­ния и оптимизационные модели.

Заключение в системном анализе должно быть науч­ной основой реализации природоохранных проектов и указывать инструменты оптимизации состояний экосистем. Изучение любой экосистемы может продолжаться бесконеч­но долго. Однако каждый исследовательский проект должен иметь конечную цель и рано или поздно завершаться. В итоге должны намечаться перспективы будущих исследований.

Приведенная схема системного подхода к изучению экосис­тем, разумеется, не является универсальной и может быть моди­фицирована в зависимости от цепей и задач проекта, а также объема информационного обеспечения.

Дата добавления: 2014-11-18