Загальний підхід до розв’язання СЛАР наближеними методами

Постановка задачі та класифікація методів

НАБЛИЖЕНІ МЕТОДИ РОЗВ'ЯЗАННЯ СЛАР НА ЕОМ

Лекція №3

До наближених методів відносяться методи, які дозволяють розв’язок системи отримати як границю послідовних k розв’язків системи (2.1) при виду:

, (3.1)

де 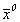- вектор розв’язку 0-го наближення, - вектор розв’язку 1-го наближення і т.д., 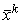- вектор розв’язку к-го наближення.

Для розв’язання СЛАР наближеними методами найбільшу цікавість представляють такі методи:

 метод послідовних наближень;

 метод Гауса-Зейделя;

 метод верхньої релаксації.

Розглянемо особливості загального підходу до розв’язання СЛАР наближеними методами.

Розглянемо систему лінійних алгебраїчних рівнянь виду:

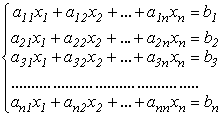(3.2)

Для розв’язання системи (3.2) методами послідовних наближень необхідно виконати наступні кроки:

1) Кожне рівняння системи розділити на діагональний елемент а _kk, де k=1,2...n, n – кількість рівнянь в системі, і перетворити кожне рівняння системи відносно координат вектора, індекс якого співпадає з номером рівняння:

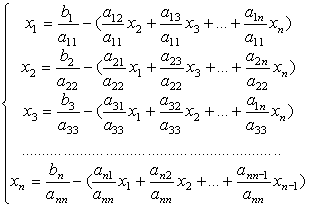(3.3)

2) Нехай 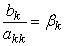, а 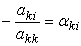, де k=1,2…n; i=1,2…n. Тоді система (3.3) матиме вигляд:

(3.4)

Така система називається зведеною до нормального вигляду.

3) Представимо систему (3.4) в матричному вигляді:

, (3.5)

або векторному

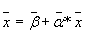. (3.6)

Якщо деяким чином визначити, так званий, вектор початкових значень , який знаходиться в правій частині (3.6), то можна отримати певні значення вектора .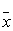

В якості вектора початкових наближень вибирають:

 вектор, в якого всі координати х_і дорівнюють 0;

 вектор, в якого всі координати х_і дорівнюють 1;

 вектор, координати якого дорівнюють координатам вектора вільних членів ;

 координати вектору 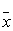вибирають в результаті аналізу особливостей об’єкту дослідження та задачі, яка розв’язується.

4) Якщо вектор початкових наближень підставити в праву частину системи (3.5) або (3.6), то вона прийме вигляд:

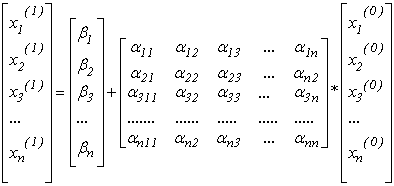
aбо ,

легко розв’язується, тому що в правої частині містить всі визначені елементи, і дозволяє отримати розв’язок системи, який називається вектором першого наближення .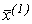

5) Перевіряється виконання умови закінчення ітераційного процесу пошуку розв’язку системи (3.2) виду:

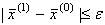(3.7),

де 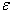- задана похибка результатів розв’язання задачі.

Якщо умова (3.7) не виконується, то 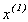підставляється в праву частину (3.5) або (3.6) і знаходиться 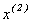з системи виду:

aбо .

6) Знову перевіряється виконання умови закінчення ітераційного процесу пошуку розв’язку системи (3.2)

.

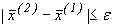Якщо умова не виконується, то підставляється в праву частину (3.5) і знаходиться 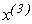з системи виду:

.

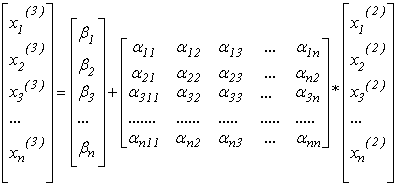і т.д.

7) Етапи 4 та 5 повторюються до тих пір поки на якому-небудь к - ому кроці не виконується умова

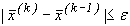. (3.8)

Таким чином, процес пошуку розв’язку системи (3.2) наближеними методами з заданою похибкою 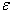є ітераційним, а умовою виходу з цього процесу є умова (3.8).

Дата добавления: 2014-11-08