Відокремлення коренів

Принципи розв’язання нелінійних рівнянь на ЕОМ

Процес розв’язання нелінійних рівнянь вигляду (4.1) або (4.2) на ЕОМ розбивається на два етапи:

1. відокремлення коренів;

2. уточнення коренів.

Перший етап іноді можна виконувати вручну, другий же виконується за допомогою спеціальних методів уточнення коренів та програм. Розглянемо особливості етапу відокремлення коренів.

Корінь 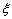рівняння , вважається відокремленим на відрізку 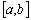, якщо на цьому відрізку дане рівняння не має інших коренів.

Відокремити корені – це означає розбити всю область допустимих значень 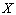(ОДЗ) на відрізки, в кожному з яких міститься один корінь (рис 4.2). Відокремлення коренів можна здійснити двома способами – графічним та аналітичним.

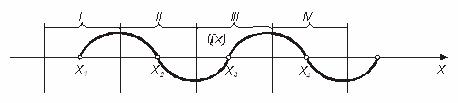
Рисунок 4.2 – Приклад розбиття ОДЗ на відрізки з єдиним коренем

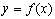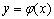Графічний метод. Будують графік функції для рівняння виду або представляють рівняння у вигляді та будують графіки функцій та 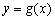. Значення дійсних коренів рівняння є абсцисами точок перетину графіка функції 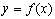з віссю 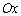або абсцисами точок перетину графіків функцій 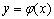та 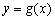. Відрізки, в яких знаходиться тільки по одному кореню, легко знаходяться наближено.

Приклад 4.1. Знайти наближено графічним способом корені рівняння .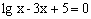

Розв’язок. Перепишемо рівняння наступним чином: Функції в лівій і правій частині рівняння мають спільну область визначення: інтервал 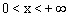. Тому будемо шукати корені саме на цьому інтервалі.

Будуємо графіки функцій 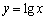і 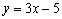(рис. 4.3).

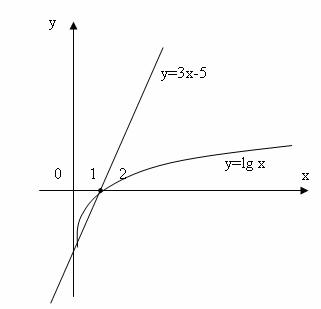
Рисунок 4.3 – Графічна інтерпретація прикладу 4.1

Пряма 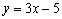перетинає логарифмічну криву в двох точках з абсцисами х1 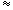0.00001 і х2 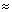1.75. На рисунку 4.4 важко показати перетин графіків цих двох функцій в першій точці, але, враховуючи, що нижня вітка логарифмічної кривої необмежено прямує до осі Оу, можливо уявити, що перетин цих двох графіків пройде поблизу точки перетину графіка функції 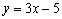і осі Оу. Абсциса точки перетину наближено дорівнює 0.00001. Отже корені рівняння х₁ 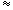0.00001 і х₂ 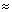1.75.

Рисунок 4.4 – Графічна інтерпретація прикладу 4.1

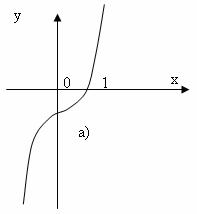
Рисунок 4.5.a – Графічна інтерпретація прикладу 4.2

Приклад 4.2. Розв’язати графічно рівняння х³-2х²+2х-1=0.

Розв’язок. Перший спосіб: Побудуємо графік функції y=x³-2x²+2x-1 і визначимо абсциси точок перетину цього графіка з віссю Ох. Крива перетинає Ох в точці х=1, звідси витікає, що рівняння має один корінь (рис.4.5.а). (Відмітимо, що алгебраїчне рівняння третього степеня має один або три дійсних кореня. Так як крива перетинає вісь абсцис тільки в одній точці, то дане рівняння має тільки один дійсний корінь. Інші два кореня - комплексні.)

Другий спосіб: Представимо дане рівняння в вигляді х³=2х²-2х+1 і побудуємо графіки функцій y=х³ і y=2х²-2х+1. Знайдемо абсцису точки перетину цих графіків; отримаємо х=1 (рис.4.5.б), або область, де знаходиться точка перетину (тобто корінь рівняння).

Приклад 4.3. Знайти графічно корені рівняння .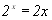

Розв’язок. Будуємо графіки функцій 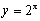та 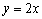. Ці графіки перетинаються в двох точках, абсциси яких рівні. Дане рівняння має два кореня 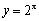та 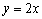. (рис.4.6).

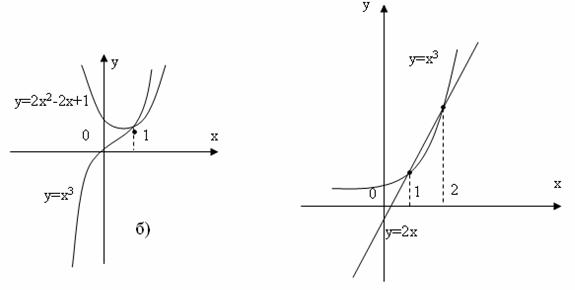
Рисунок 4.5.б – Графічна Рисунок 4.6 – Графічна

інтерпретація прикладу 4.2 інтерпретація прикладу 4.3

Аналітичний метод. Аналітично корні рівняння можна відокремити, використовуючи деякі властивості функцій та однією з розглянутих нижче теорем.

Теорема 1. Якщо функція неперервна на відрізку 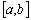і приймає на кінцях цього відрізку значення різних знаків, то всередині відрізка 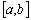існує хоча б один корінь рівняння (рис.4.7).

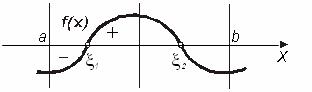
Рисунок 4.7 – Графічна інтерпретація теореми 1

Теорема 2. Якщо функція 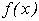неперервна та монотонна на відрізку 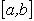і приймає на кінцях відрізка значення різних знаків, то всередині відрізка 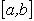існує корінь рівняння 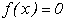, і цей корінь єдиний (рис.4.8.а).

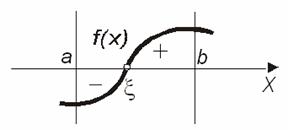
Рисунок 4.8.а – Графічна інтерпретація теореми 2

Теорема 3. Якщо функція неперервна на відрізку 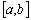і приймає на кінцях цього відрізку значення різних знаків, а похідна 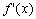зберігає постійний знак всередині відрізка, то всередині відрізка існує єдиний корінь рівняння (рис.4.8.б).

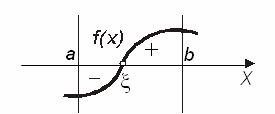
Рисунок 4.8.б – Графічна інтерпретація теореми 3

Для відокремлення коренів аналітичним методом можна рекомендувати наступний алгоритм:

1. Дослідити дане рівняння на монотонність і неперервність, визначити область допустимих та граничних значень.

2. Знайти 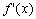– першу похідну, прирівняти її до нуля та знайти критичні точки.

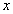3. Скласти таблицю знаків функції , використовуючи для значення критичних точок, граничних значень з ОДЗ і точок, отриманих на першому кроці при аналізі даного рівняння.

4. Визначити інтервали, на кінцях яких функція приймає значення протилежних знаків. Всередині цих інтервалів існує по одному і тільки одному кореню.

Приклад 4.4. Відокремити корені рівняння x³+3x²-24x+1=0

Розв’язок.

1. ОДЗ рівняння (- )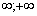

2. Визначимо першу похідну функції f(x): f'(x)=3x²+6x-24 та критичні точки, для чого f'(x)=0: x₁=-4; x₂=2

3. Складемо таблицю знаків виду

x	-	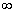-4	2	+
Sign f(x)	-	+	-	+

В результаті аналізу таблиці отримаємо три відрізка на яких функція змінює знак: (- 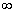,-4], [-4,2], [2, ).

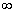Розширимо таблицю, щоб отримати точні значення кінців відрізків

x	-	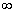-7	-6	-5	-4	-3	-2	-1	0	1	2	3	4	+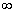
Sign f(x)	-	-	+	+	+	+	+	+	+	-	-	-	+	+

Аналіз таблиці дозволяє обрати три відрізка, на яких функція f(x) змінює знак.

4) Наступним етапом дослідження рівняння на ЕОМ є етап уточнення значення кореня з заданою 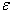на кожному відрізку.

Дата добавления: 2014-11-08