Чисельні методи розв’язання систем нелінійних рівнянь

Достатньо велика кількість інженерних задач на проміжному етапі вирішення зводиться до вирішення системи нелінійних рівнянь. Це одна з найважчих задач з точки зору реалізації її на ЕОМ. Одним із найбільш простих алгоритмів її рішення є метод Ньютона. Це найбільш розповсюджений метод розв’язання систем нелінійних рівнянь. Його популярність обумовлена тим, що в порівнянні з методом простої ітерації він забезпечує найбільш швидку збіжність. В основі методу Ньютона лежить представлення всіх n рівнянь у вигляді рядів Тейлора.

Розглянемо алгоритм методу Ньютона.

Нехай дана система нелінійних рівнянь виду

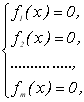(4.20)

де – неперервно-диференційні функції.

2. Алгоритм методу базується на розкладі кожної функції системи в околі точки з координатами в ряд Тейлора.

члени рядів вищих порядків ( тощо).

1. Початкова система буде мати вигляд:

(4.21)

2. Припустимо, що прирости 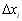вибрані таким чином, що точки з координатами 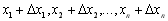є коренями даної системи рівнянь з заданим степенем наближення 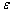. Тоді ліву частину рівнянь системи (4.21) можна прирівняти до нуля, тобто система рівнянь (4.21) буде мати вигляд:

(4.22)

Або в матричній формі система (4.22) буде мати вигляд:

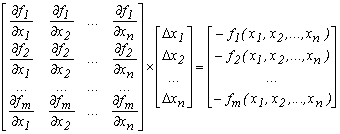(4.23)

де – матриця Якобі.

3. В результаті таких перетворень система рівнянь може розглядатися як система лінійних алгебраїчних рівнянь відносно 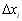. В такому випадку, якщо врахувати, що заданий вектор х початкових наближень виду:

,

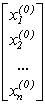можливо розв'язувати систему відносно вектора приросту 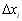, та знайти розв'язок системи, як сума попереднього значення та вектора :

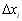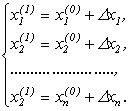(4.24)

Дану задачу можна розв'язати з будь-якої точки, вибравши вектор початкових наближень.

4. Процес розв’язання системи нелінійних рівнянь (4.20) з використанням системи лінійних алгебраїчних рівнянь (4.23) відносно 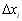- ітераційний, та буде продовжуватись до тих пір, поки всі координати вектору приростів не стануть менше за абсолютною величиною заданої похибки 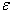, тобто .

Схема алгоритму метода Ньютона представлена на рисунку 4.20.

Рисунок 4.20 – Схема алгоритму розв'язання систем нелінійних рівнянь методом Ньютона

Приклад. Стійкість складної конструкції жорстких балок описується системою нелінійних рівнянь виду:

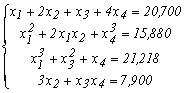
Розв’язати дану систему нелінійних рівнянь методом Ньютона.

Розв’язок. Для того, щоб розв’язати дану систему нелінійних рівнянь методом Ньютона необхідно перетворити систему до вигляду (4.23). Для цього знайдемо спочатку частині похідні всіх рівнянь системи в початкової точці для формування матриці Якобі, яка буде мати вигляд:

За допомогою програми, що складена відповідно алгоритму, який представлений на рисунку 4.20, для знаходження вектора розв’язку Х багаторазово методом Гауса розв’яжемо на ЕОМ систему виду:

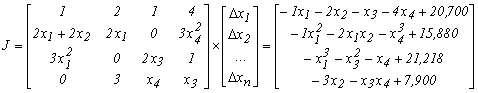
відносно вектору поправки з початковими значеннями змінних та з заданою похибкою , з яких починається ітераційний процес.

В результаті можна отримати наступні результати:

Номер ітерації
0	1.0000	1.0000	1.0000	1.0000
1	2,75037	4,6763	7,8958	0,1753
2	1,3448	5,2971	5,9494	0,7029
3	1,4775	3,8437	4,3419	1,7983
4	1,5427	6,2434	4,1204	0,6376
5	1,2364	5,7274	4,3436	0,9163
6	1,2024	5,5986	4,2995	1,0002
7	1,2000	5,6000	4,3000	1,0000
8	1,2000	5,6000	4,3000	1,0000

Дата добавления: 2014-11-08