Метод найшвидшого спуску

Даний метод заснований на використанні ітераційної формули

,

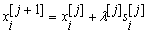де 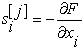, причому усі похідні обчислюються при ;

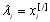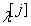- величина кроку, значення якого змінюється (зменшується або обчислюється) методом половинного ділення.

Алгоритм методу найшвидшого спуску:

1. Обираємо початкові значення координат вектора 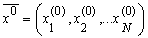і початкові значення кроку ітераційного процесу , які звичайно обираються з умов розв’язуємої конкретної задачі. Хоча загальних правил вибору 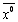немає, однак якщо є додаткова інформація про область розташування мінімуму цільової функції, то 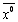обираємо в цій області.

2. Задаємо номер ітерації к = 1.

3. Обчислюємо значення цільової функції в точці з координатами .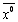

4. Обчислюємо значення градієнта .

5. Обчислюємо норму вектора градієнта NG.

6. Якщо |NG| < заданої 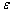, то ітераційний процес закінчується і оптимум знайдений.

7. Якщо умова |NG| < 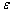не виконується, то визначаються нові координати вектора 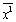, які отримуються при русі до мінімуму цільової функції з кроком (рис. 14.5).

8. Порівнюємо два значення цільової функції в двох точках з координатами векторів 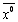і 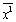за формулою

Рисунок 14.5– Послідовність руху до мінімуму з заданим кроком

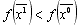, (14.31)

9. Якщо умова не виконується, то крок був вибраний невірно, тобто з цим кроком перескочили через оптимум і крок потрібно зменшити, наприклад в два рази 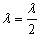і переходимо до пункту 7 (рис. 14.5).

10. Якщо умова (14.31) виконується, то запам’ятовуємо координати вектора 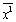і переходимо до пункту 4.

Схема алгоритму описаного методу представлена на рис. 14.6.

Дата добавления: 2014-11-08