Энтропия. Все формулировки второго начала термодинамики сводятся к тому, что самопроизвольные процессы необратимы

Все формулировки второго начала термодинамики сводятся к тому, что самопроизвольные процессы необратимы, т.е. не могут протекать в обратном порядке без изменения состояния окружающих тел.

Необратимость тепловых процессов с молекулярно-кинетической точки зрения объясняется их вероятностным характером. Равновесное состояние осуществляется наибольшим числом способов реализации этого состояния. В качестве примера рассмотрим систему, состоящую из четырех частиц газа: a, b, c, d (рис. 8.9). Эти частицы находятся в объеме, разделенном мысленно на две равные ячейки, и могут свободно в них перемещаться.

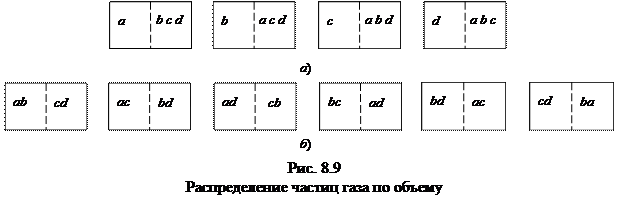Состояние системы, определяемое числом частиц в первой и второй ячейках, назовем макросостоянием; состояние системы, определяемое тем, какие конкретно частицы находятся в каждой из ячеек, - микросостоянием. Тогда (рис. 8.9. а) макросостояние – одна частица в первой ячейке и три частицы во второй – осуществляется четырьмя микросостояниями, а макросостояние, соответствующее размещению четырех частиц, равномерно по две в каждой ячейке, - шестью микросостояниями (рис. 8.9, б).

Термодинамической вероятностью W_тер называют число способов размещения частиц или микросостояний, реализующих данное макросостояние.

В приведенных выше примерах W_тер=4 в первом случае и W_тер=6 во втором. Очевидно, что равномерному распределению частиц по ячейкам (по две) соответствует большая термодинамическая вероятность. С другой стороны, равномерное распределение частиц отвечает равновесному состоянию. Из теории вероятности известно, что система, предоставленная самой себе, стремится прийти к макросостоянию, которое реализуется наибольшим количеством способов, наибольшим количеством микросостояний, т.е. к состоянию с наибольшей термодинамической вероятностью.

Таким образом, количественной характеристикой теплового состояния является термодинамическая вероятность. Однако принято вместо W_тер пользоваться величиной

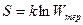(8.10.1)

называемой энтропией системы.

Соотношение (8.10.1), характеризующее связь энтропии и термодинамической вероятности называется формулой Больцмана. Отсюда определение энтропии: энтропия – скалярная физическая величина, характеризующая макросостояние термодинамической системы, и численно равная постоянной Больцмана, умноженной на 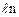термодинамической вероятности этого состояния.

Соответственно второе начало термодинамики может быть сформулировано так: все естественные процессы в изолированной термодинамической системе протекают так, что система переходит от состояний, менее вероятных, к состояниям, более вероятным.

Изменение термодинамической вероятности .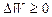

Понятие энтропии впервые было введено Р.Клаузиусом в 1862 году. Для выяснения физического содержания этого понятия рассматривают отношение теплоты Q, полученной телом в изотермическом процессе, к температуре Т теплоотдающего тела, называемое приведенным количеством теплоты:

dS = 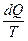, (8.10.2)

где dQ –бесконечно малое количество теплоты, сообщенное системе в элементарном обратимом процессе.

Для произвольного процесса приведенное количество теплоты равно:

ΔS =S₂ - S₁= 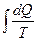, (8.10.3)

где dQ – количество теплоты, сообщенное системе на элементарном участке процесса теплоотдающим телом, температура которого Т; S₁ и S₂ – значения энтропии в состояниях 1 и 2, DS – изменение энтропии в течение обратимого процесса. Изменение энтропии в любом обратимом процессе, переводящем систему из состояния 1 в состояние 2, равно приведенному количеству теплоты, переданному системе в этом процессе.

Изменение энтропии системы, с учетом (8.10.1):

,

где W₁ и W₂ - значения термодинамической вероятности в состоянии 1 и 2.

Каждому состоянию тела соответствует одно определенное значение энтропии. Поэтому энтропия является однозначной функцией состояния. Физический смысл имеет не сама энтропия, а лишь разность энтропий.

Р. Клаузиусом были получены следующие важные положения, которые сформулируем без доказательства:

1. Энтропия является аддитивной величиной: энтропия системы из нескольких тел является суммой энтропий всех тел.

2. Энтропия определяется только с точностью до произвольной постоянной.

3. Если в изолированной системе происходят обратимые процессы, то ее энтропия остается неизменной .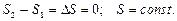

4. Энтропия изолированной системы при протекании необратимого процесса возрастает. Энтропия изолированной системы не может уменьшаться ни при каких процессах.

5. Энтропия системы, находящейся в равновесном состоянии, максимальна.

Математически эти положения можно записать в виде неравенства называемого неравенством Клаузиуса:

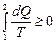или 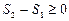(8.10.4)

В природе все реальные процессы являются необратимыми. Поэтому можно утверждать, что все процессы в конечной изолированной системе ведут к увеличению энтропии. Это принцип возрастания энтропии. Основываясь на вышеизложенном, можно так сформулировать второе начало термодинамики: в изолированных системах возможны лишь такие процессы, при которых энтропия не убывает. Она постоянна, если процессы обратимы, и возрастает, если процессы необратимы.

Если система не изолирована, то ее энтропия может вести себя произвольным образом. Если система отдает тепло (DQ<0), то ее энтропия убывает. Если такая система совершает замкнутый цикл, то энтропия в конце цикла буде равна исходному значению, то есть ее изменение равно нулю. Однако на разных этапах энтропия может и убывать, и возрастать, но так, что сумма всех изменений энтропии равно нулю.

Энтропия является мерой беспорядка системы.

Так как энергия беспорядочного движения частиц газа пропорциональна температуре, то при нуле температуры беспорядочное движение должно прекратиться – частицы будут располагаться наиболее упорядоченным образом. Этой наибольшей упорядоченности расположения частиц должна отвечать наименьшая энтропия. В.Нернст (1864-1941), основываясь на ряде физико-химических наблюдений, высказал положение, часто называемое третьим началом термодинамики: энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина:

.

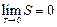Из теоремы Нернста следует, что теплоемкости С_р и С_V при 0 К равны нулю.

Дата добавления: 2014-11-18