Вектор электрического смещения. Теорема Гаусса для электростатического поля в диэлектрике

Источником электростатического поля являются свободные и свя­занные электрические заряды: линии напряженности электрического по­ля начинаются на положительных зарядах (или в бесконечности) и окан­чиваются на отрицательных (или в бесконечности).

Однако при решении задач, связанных с электрическим полем в ди­электрике, в ряде случаев оказывается более удобным учитывать только поле свободных зарядов. Для этого вводится понятие вектора электри­ческого смещения (). Аналогично, как и поле напряженности, поле электрического смещения изображается с помощью линий электрического смещения, направление и густота которых определяется точно так же, как и для линий напряженности.

Рассмотрим изменение электрического поля на достаточно протяженной границе двух однородных и однородно поляризованных диэлектриков 1 и 2 (рис. 10.23).

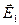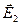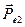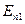В первом диэлектрике напряженность электрического поля и вектор поляризации соответственно равны и , во втором диэлектрике — и . В общем случае все эти четыре вектора произволь­но ориентированы в диэлектриках, поэтому можно говорить об их танген­циальных к границе раздела (, , , ) и нормальных (, , , ) составляющих. На границе возникнут связанные электрические заряды противоположных знаков, поверхностные плотности которых рав­ны σ_св1 и σ_св2. Эти заряды создадут электрическое поле, напряженность ко­торого

Напряженность Е^/ уменьшит нормальную составляющую напряжен­ности электрического поля в одном диэлектрике и увеличит в другом, поэтому разность нормальных составляющих напряженности равна

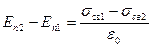
учитывая, что поверхностная плотность связанных зарядов равна поляризованности

или

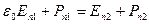
Из формулы видно, что на границе двух диэлектриков сохраняется нормальная составляющая, т.е.

Данное условие означает, что поток вектора электрического смеще­ния не изменяется на границе двух диэлектриков, т. е. линии этого вектора (рис. 10.23) не начинаются и не заканчиваются на связанных зарядах. Через область поля, где находятся связанные заряды, линии вектора электрического смещения проходят не прерываясь.

Следовательно,

(10.10.1)

Это и есть вектор электрического смещения.

В скалярной записи

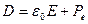
учитывая, что поляризованность пропорциональна напряженности, т.е.

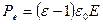
получим

или в векторной форме

(10.10.2)

Данная формула показывает взаимосвязь электрического смещения и напряженности поля.

Для произвольной замкнутой поверхности S поток вектора сквозь эту поверхность

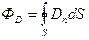
где D_n – проекция вектора на нормаль n к площадке d S.

Теорема Гаусса для электростатического поля в диэлектрике:

(10.10.3)

т.е. поток вектора электрического смещения сквозь замкнутую поверхность равен алгебраической сумме свободных зарядов, находящихся внутри этой поверхности.

Для вакуума (диэлектрическая постоянная равна единице), тогда поток вектора напряженности сквозь произвольную замкнутую поверхность равен

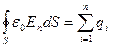или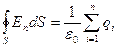

Так как источниками поля в среде являются как свободные, так и связанные заряды, то теорему Гаусса для поля в общем виде можно записать как

где - соответственно алгебраические суммы свободных и связанных зарядов, охватываемых замкнутой поверхностью S.

Дата добавления: 2014-11-18