Затухающие колебания. Логарифмический декремент затухания

В реальном случае на колеблющееся тело действуют силы сопротивления (трения), характер движения изменяется и колебание становится затухающим. При не очень больших амплитудах и частотах эта сила трения пропорциональна скорости и направлена в противоположную сторону движения:

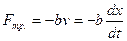, (15.4.1)

где 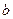– коэффициент трения, характеризующий свойства среды оказывать сопротивление.

Тогда уравнение движения, согласно второму закону Ньютона

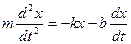(15.4.2)

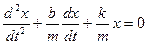(15.4.2, а)

Обозначим

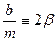
Тогда

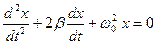(15.4.2, б)

Подстановка в (15.4.2, б) функции х = e ^{λ t} приводит к характеристическому уравнению

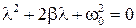(15.4.3)

Корни этого уравнения равны

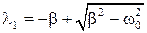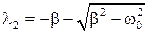, . (15.4.4)

При не слишком большом затухании (при β<ω₀) подкоренное выражение будет отрицательным. Представим его в виде (iω)², где ω - величина, равная

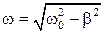. (15.4.5)

Тогда корни характеристического уравнения запишутся следующим образом:

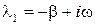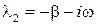, . (15.4.6)

при не слишком сильном затухании общее решение уравнения (15.4.2,б) имеет вид

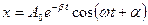
, (15.4.7)

где А ₀ - амплитуда колебаний в начальный момент времени.

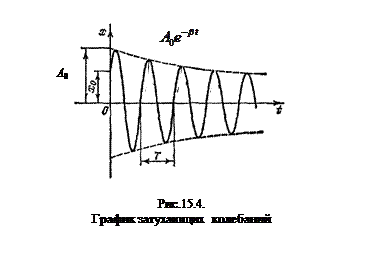На рисунке дан график (15.4.) затухающих колебаний. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки x.

В соответствии с видом функции (15.4.7) движение системы можно рассматривать как гармоническое колебание частоты ω с амплитудой, изменяющейся по закону А (t) = А ₀ e ^{‑β∙ t} .

Скорость затухания колебаний определяется величиной β = b /2 m, которую называют коэффициентом затухания. Найдем время τ, за которое амплитуда уменьшается в e раз. По определению e ^‑β∙τ = e ^‑1, откуда β∙τ = 1. Следовательно, коэффициент затухания обратен по величине тому промежутку времени, за который амплитуда уменьшается в e раз.

Период затухающих колебаний равен

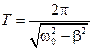. (15.4.8)

При незначительном сопротивлении среды 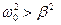, период колебаний практически равен T ₀ = 2π/ω₀. С ростом коэффициента затухания период колебаний увеличивается.

Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно

.

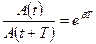Это отношение называют декрементом затухания, а его логарифм — логарифмическим декрементом затухания:

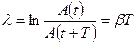(15.4.9)

Логарифмический декремент характеризует затухание колебаний за период. Пусть 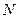– число колебаний, после которых амплитуда уменьшается в e раз, а 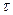- промежуток времени, соответствующий этому уменьшению. Тогда 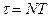, , 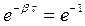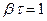и

,

.

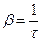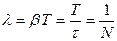Таким образом, 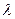– есть величина, обратная числу колебаний, по истечении которых амплитуда спадает в e раз. Например, если это значит, что амплитуда колебаний уменьшается в e раз по истечении 100 колебаний. Зная 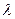, можно определить коэффициент трения :

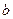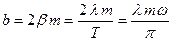(15.4.10)

Дата добавления: 2014-11-18