Тема 2. Методика навчання нумерації чисел від 1 – 10 та числа 0

Наочні посібники та дидактичний матеріал.

Демонстраційні: набір карток з числовими фігурами; набір карток з цифрами і арифметичними знаками; набір геометричних фігур різного кольору і розміру; таблиця “Числові сходи”, що складається протягом вивчення нових чисел; круги, що повертаються, для вивчення складу чисел; картки для вивчення складу чисел;

Індивідуальні: картки з цифрами і знаками; числові фігури; набір геометричних фігур; набір монет.

Одним з основних розділів курсу математики в 1-му класі є „Числа 1—10 та число 0”. Поняття “число” відноситься до первинних, невизначуваних понять математичної науки. Натуральне число – це незмінна загальна властивість, що характеризує клас скінчених еквівалентних множин. Поняття “натуральне число” спирається на поняття “множина”, “еквівалентність”, “взаємно-однозначна відповідність”, їх слід враховувати при введенні кожного числа.

Натуральні числа не можна ані побачити, ані почути, ані доторкнутися до них, тобто вони недоступні органам чуття. Мабуть, єдина можливість зробити їх „реальними” – записати. В основі формування поняття числа в школі лежить лічба предметів. Лічба – це встановлення взаємно-однозначної відповідності між елементами заданої кінцевої множини і числами – елементами початкового відрізку натурального ряду.

Число виступає як результат лічби, тобто назване останнім при лічбі характеризує кількість предметів поданої сукупності. Крім того, в основі операції лічби лежить встановлення взаємооднозначної відповідності між предметами певної сукупності та словами-числівниками, які називають початковий відрізок натурального ряду. Тому кожне число, назване при лічбі, характеризує не лише кількість сукупності, але й порядок предметів при лічбі.

Вивчення чисел за різними методичними системами має свої особливості. Наприклад існує підхід коли кожне число вводиться окремо або вивчення чисел подається групами: від 1 до 5 і від 6 до 10. Так, Л.П. Кочина пояснює необхідність вивчення чисел групами тим, що діти шестирічного віку, в переважній більшості, лічать у межах 10, знають цифри і вміють співвідносити числа з відповідними предметними множинами. Тому вивчення групи чисел, а не кожного числа окремо підвищує інтерес учнів до навчання, створює можливості для застосування варіативних завдань і динамічнішої побудови уроків.

З наведених доказів можна зробити висновок, що вивчення чисел групами доцільно використовувати в разі, якщо учні прийшли до школи більш підготовленими.

Послідовне ознайомлення з числами від 1 до 10 (за методичною системою М.В. Богдановича) має сенс для менш підготовлених до школи учнів.

При формуванні поняття про кожне окреме число система завдань будується за планом:

- формування поняття про число як кількісну характеристику класу кінцевих еквівалентних множин;

- позначення числа цифрою: друкована та прописна цифра;

- утворення числа з попереднього;

- навчання написання цифри;

- співвіднесення числа та кількості предметів і навпаки;

- лічба в прямому та оберненому порядку в межах даного числа;

- порівняння чисел;

- склад числа.

Розглянемо докладніше методичні особливості вивчення нумерації чисел першого десятка, оскільки основні питання (утворення числа, написання цифри, співвіднесення цифри з групою предметів і, навпаки, ознайомлення з місцем числа в натуральному ряді чисел, порівняння і склад чисел), з якими ознайомлюються учні, є характерними для вчених, які представляють різні методичні підходи.

Утворення числа як кількісної характеристики класу кінцевих еквівалентних множин

Число вводиться як кількісна характеристика класу скінчених еквівалентних множин. Наприклад, покажемо, як вводиться число 5 на підставі аналізу і порівняння сукупностей геометричних фігур.

На дошці чи набірному полотні виставлено рядками 5 кругів, 5 квадратів, 5 трикутників та 5 п’ятикутників, що відрізняються за кольором, розміром тощо. Визначаючи спільну властивість усіх цих фігур, діти визначають, що їх однакова кількість: кругів стільки ж, скільки й квадратів; квадратів стільки ж, скільки й трикутників, трикутників стільки, скільки п’ятикутників і так далі, пояснюючи це так: якщо складемо пари, наприклад, із кругів і трикутників, то кожному кругу відповідатиме один трикутник, а кожному трикутнику відповідатиме один квадрат. Виходячи з цього, діти роблять загальний висновок: усіх фігур порівну.

Нове число утворюється на підставі прирахування 1 до попереднього числа. Учитель забирає 1 круг і запитує: „Тепер кругів стільки ж, скільки й інших фігур?” (Ні), „А скільки?” (4), – „Що треба зробити, щоб кругів стало стільки ж, скільки й інших фігур?” (Треба до 4-х кругів добавити ще 1.) – „Таким чином, ми одержали число 5, що характеризує кількість кругів, квадратів, трикутників й п’ятикутників!”, „Число „п’ять” безпосередньо слідує після числа „чотири.”.

Далі вчитель уточнює, яке попереднє число перед числом „5”, як одержати число з попереднього; яке наступне число в числовому ряді за числом „5”, як одержати його з наступного. У результаті виконання системи аналогічних завдань учні можуть дістати висновку: щоб одержати число, треба до попереднього додати 1 або з наступного числа відняти 1.

Навчання написанню цифри, яка позначає на письмі дане число

Число “п’ять” на письмі позначається спеціальним значком – цифрою, яка має таку ж саму назву: “5” – цифра “п’ять”. Учитель демонструє друковану і прописну цифру “п’ять”. Діти показують у підручнику (на таблиці, у зошиті з друкованою основою) друковану цифру „п’ять”; показують прописну цифру „п’ять”.

Далі розглядаємо елементи цифри “5”. Цифра “п’ять” складається з трьох елементів: похилої і горизонтальної паличок і правого напівовала. Спочатку пишемо похилу паличку, а потім правий напівовал і лише потім пишемо горизонтальну паличку.

На цьому етапі можна запропонувати учням „цифри-шершавчики” – картки з цифрою, що виготовлена з наждачного паперу і наклеєна на гладенький картон. Діти проводять по шершавій цифрі пальцем спочатку з відкритими очима, а потім – із закритими. Якщо вони опиняться на гладенькому папері, то припустилися помилки. Таким чином, діти запам’ятовують напрямок руху руки при написанні цифри.

Далі згадуємо вірш про цифру „п’ять” і прописуємо її у повітрі: спочатку пишемо похилу паличку, потім правий напівовал і лише потім горизонтальну паличку. І, нарешті, діти спочатку обводять в зошиті з друкованою основою цифру „п’ять”, промовляючи назви елементів, з яких вона складається, у тому порядку, як треба їх писати, а потім самі пишуть цифру в зошитах із друкованою основою та у звичайних зошитах у клітинку.

Отже, при вивченні кожної цифри робота проходить у такій послідовності: розгляд зразка написання друкованої і прописної цифри у підручнику, на таблиці чи в зошиті з друкованою основою; пояснення і показування письма цифри учителем на дошці; написання цифри в повітрі; написання цифри в зошитах, спочатку по пунктирних лініях, а потім самостійно.

Навчання співвіднесення цифри та числа предметів; числа предметів і цифри

Для лічби предметів застосовують числа, а для того, щоб записати числа на дошці або в зошиті, використовують спеціальні позначки – цифри.

Перед учнями ставиться завдання: позначити цифрою кількість предметів, що викладено на набірному полотні. Наприклад, учитель виставив три великі і дві маленькі зірочки різного кольору. Учням пропонується показати цифру, яка означає кількість усіх зірочок, кількість маленьких зірочок, кількість блакитних зірочок тощо.

Корисні з точки зору розвитку дрібної моторики завдання, в яких вимагається обвести стільки клітинок у зошиті, скільки вказано цифрою (5, 2, 1); покласти на парту стільки зелених кружечків, скільки позначено цифрою (1, 4, 2). На цьому етапі можна пропонувати дітям не лише завдання на позначення кількості об’єктів цифрою, але й на запис цієї цифри.

Означення місця числа в натуральному ряду

Учні називають числа, що йдуть у натуральному ряду до певного числа, наприклад, числа „5”; визначають, що кожне наступне одержують з попереднього прилічуванням 1. Таким чином, кожне наступне число більше за величиною, що ілюструється на числових сходах. Учні читають за числовими сходами числа від більшого до меншого або від меншого до більшого.

Послідовність чисел початкового відрізку натурального ряду доцільно ілюструвати й на числовому промені:

1 2 3 4

Пропонуємо школярам завдання типу: по числовому променю назвіть числа в прямому (зворотньому) порядку; назвіть наступне число після числа, наприклад, „3”; назвіть попереднє число до числа, наприклад, „5”; назвіть наступне і попереднє числа до числа, наприклад „4”; назвіть сусідів числа „2”; після якого числа йде число „5”; яке число стоїть перед числом „4”; яке число стоїть між числами „2” і „4”?

Розв’язуючи такі завдання, учні поступово знайомляться з властивостями натурального ряду чисел: в натуральному ряду всі числа впорядковані – кожне наступне число більше на 1, а кожне попереднє, навпаки, менше на 1; найменше натуральне число 1.

Порівняння чисел різними способами

На підставі порівняння сукупностей об’єктів способом утворення пар учні знайомляться з рівночисельними та нерівночисельними множинами, зі знаками „рівно”, „не рівно”. Коли порівнюються рівночисельні сукупності або рівні числа, з’ясовується відношення рівності, то ставиться знак “=”. Для того, щоб пояснити учням, чому саме цей знак обраний для позначення рівності, вчитель звертає увагу на те, що цей знак складається з двох відрізків однакової довжини.

У подальшому навчанні діти знайомляться з написанням знака порівняння: „більше”, „менше”. Зазначимо, що, пояснюючи запис результату порівняння за допомогою знаків “більше”, “менше”, треба звернути увагу школярів на те, що це один і той же знак, тільки перекинутий. Знак ставиться так, щоб більше число знаходилося з того боку, де відстань між кінцями більша. Або можна застосувати аналогію з пташками: мама-пташка годує маленьких пташенят із дзьобика, тому до меншого числа знак ставимо “дзьобиком”.

Спосіб утворення пар. Наприклад, треба порівняти числа 3 і 4. Діти викладають на парті стільки кружечків, скільки вказує цифра “3”; під кружечками викладають стільки трикутників, скільки вказує цифра “4”; складають пари з кружечків і трикутників; з'ясовують, які фігури лишилися без пари – їх більше; яких фігур не вистачило для утворення пар – їх менше. Запис нерівності діти читають двома способами: три менше чотирьох. Чотири більше трьох.

Цей спосіб порівняння чисел використовується в період ознайомлення з числами першого п’ятка.

Спосіб порівняння за місцем числа в натуральному ряду. Порівняння здійснюються на підставі застосування правила: “Число, яке йде при лічбі раніше (пізніше) даного числа, завжди менше (більше) цього числа”. Наприклад, треба порівняти числа „5” та „7”: число „5” при лічбі називається раніше, ніж число „7”, тому „5” менше „7”; число „7” при лічбі називається пізніше, ніж „5”, тому „7” більше за „5”.

Логічний спосіб міркування здійснюються на підставі знання складу чисел. Наприклад, треба порівняти числа „5” та „4”: число „5” – це „4” та ще „1”, „4” та ще „1” більше чотирьох, тому п’ять більше чотирьох. Порівняємо числа „4” та „5”: „4” – це „5” без 1-го, „5” без 1-го менше п’яти, тому „4” менше 5-ти.

Вивчення складу чисел

На етапі вивчення нумерації в межах 10-ти склад чисел за системою Л.П. Кочиної не вивчається. Ця тема переноситься на більш пізній термін, коли діти набудуть глибших уявлень про число, і опрацьовуватиметься разом з темою „Додавання і віднімання у межах 10”.

За методичною системою М.В. Богдановича, вивчення складу чисел розглядається як етап, що допомагає здійснити підготовку до розуміння дій додавання і віднімання та засвоєння таблиць додавання і віднімання в межах 10. Ознайомлення зі складом числа проводиться на предметній основі.З цією метою доцільно використовувати два різновиди вправ: розгляд окремих випадків складу числа і розгляд впорядкованої сукупності пар чисел, на які можна розкласти число.

Записуючи склад числа „5”, ми почнемо з випадку утворення числа „5” з попереднього числа „4” і „1”, а потім, подумки пересуваючи по одному кружечку, відтворимо і всі випадки складу

4 1 3 2 2 3 1 4

Розглянемо методику ознайомлення зі складом числа „5”. Учитель пропонує учням поділити робоче місце парти на дві частини – праву та ліву і взяти п’ять зелених кружечків та розташувати їх ліворуч. Пересуваючи по одному кружечку праворуч, визначаємо їх кількість окремо ліворуч та праворуч, а також загальну кількість; виходячи з цього, робимо висновок про те, що ці числа складають дане число; записуємо випадок складу числа в таблиці:

Записуючи склад числа „5”, ми почнемо з випадку утворення числа „5” з попереднього числа „4” і „1”, а потім, подумки пересуваючи по одному кружечку, відтворимо і всі випадки складу числа „п’ять”.  

5

4 1

2 3

1 4

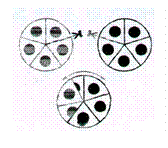Ілюструвати склад чисел можна за допомогою кругів, що обертаються. Учитель вирізає з картону два однакові круги і кожний з них ділить, наприклад, на 5 сегментів (стосовно складу числа, що вивчається); у центрі кожного сегменту розташовується якийсь малюнок – у першому крузі, наприклад, червоного кольору, а в другому – зеленого. У кожному крузі робимо розріз по радіусу. У цей розріз вставляються круги один в один, що дозволяє їх обертати.

Для запам’ятовування складу чисел корисними є завдання на складання „будиночків”, „машинок”, „потягів” зі складом чисел. Треба зазначити, що, враховуючи дані психологічної науки стосовно підвищення ефективності сприймання молодших школярів, ці таблиці корисно розташовувати горизонтально:

Для засвоєння складу чисел корисно застосовувати картки типу “доміно”: спочатку учні виконують прості вправи – визначають, скільки точок праворуч, скільки ліворуч, скільки точок усього. Далі дітям пропонується знайти лише ті картки, які ілюструють число. Наприклад: з карток „доміно” виберіть ті, що ілюструють склад числа, наприклад „5”:

Після ознайомлення з дією додавання склад числа розглядається як подання його у вигляді суми двох доданків. А після введення конкретного змісту дії віднімання учні за картками „доміно” складають не лише дві рівності на додавання, а й дві – на віднімання. Таким чином, відбувається пропедевтика переставної властивості додавання та взаємозв’язку між діями додавання і віднімання. Наприклад: 2 + 3 = 5. Зліва 2 точки, справа 3 точки; об’єднуємо точки зліва направо, буде 5 точок. 3 + 2 = 5 Справа 3 точки, зліва 2 точки; об’єднуємо точки справа наліво, отримаємо 5. 5 – 2 = 3. Всього 5 точок, виключили 2 точки (можна прикрити їх рукою), отримаємо 3 точки. 5 – 3 = 2. Всього 5 точок¸ виключили 3 точки, залишилось 2 точки.

Корисні завдання на заповнення пропусків у складі чисел і запис на цій основі рівності на додавання та віднімання:

6 – це 5 і 1. 6 – ціле. 5 і 1 – його частини. Об’єднуємо частини в ціле: 5 + 1 = 6. Виключаємо з цілого його першу частину, лишається друга частина: 6 – 5 = 1.  

	-		=
	-		=
	-		=
	-		=
	-		=

	+		=
	+		=
	++		=
	+		=
	+		=
.
.

5
	3
1
	2
	4

Число і цифра „нуль”

Тема “Числа першого десятка” закінчується вивченням числа „нуль”. Поняття про число „нуль” вводимо, як результат віднімання однакових чисел. Спосіб отримання числа „нуль” полягає у вилученні із множини всіх її елементів і запису дій над числами. Наприклад:

На гілці було 2 листочки. Подув вітер, і один листочок упав на землю. Скільки листочків залишилося? (1) Як знайшли? (Ми від 2-х відняли 1, отримали 1: 2 – 1 = 1) Ще раз подув вітер і останній листочок упав. Скільки листочків залишилося на гілці? (Нічого) А як це записати? (Треба від 1 відняти 1.) “Нічого” – це означає пуста множина предметів, тобто множина, в якій немає жодного елемента; в математиці численність такої множини відповідає числу „нуль”. Тому запишімо: 1 – 1 = 0.

А якщо б вітер зірвав відразу два листочки, скільки б залишилося листочків на гілці? (2 – 2 = 0) Учні наводять приклади, коли в результаті отримаємо число нуль: 4 – 4, 14 – 14, 100 – 100.

Далі з’ясовується, коли ми отримуємо нуль? При виконанні якої арифметичної дії? (При відніманні.) Чи завжди при відніманні ми отримуємо нуль? (Ні) А коли при відніманні отримуємо нуль? (Лише тоді, коли віднімаємо однакові числа). Школярі роблять висновок: при відніманні однакових чисел отримуємо в результаті число „нуль”.

Число „нуль” позначається цифрою, яка називається так само – “нуль – 0”.

При вивченні чисел від 0 до 9 необхідно приділяти увагу формуванню узагальненого поняття про лічильну одиницю. Для цього при розгляданні кожного числа включаються вправи на лічбу однакових груп предметів (вивчаючи число 2 – лічать пари предметів, число 3 – трійки предметів, число 4 – четвірки предметів, 5 – п’ятірки предметів й так далі). Виконуючи такі вправи, діти помічають, що корисно застосовувати групування предметів при лічбі, так можна порахувати велику кількість предметів; але результат лічби залежить від обраної лічильної одиниці.

Наприклад, на набірному полотні стоять 4 малюнки з трійками коней. Діти малюють чотири трійки точок і потім ведуть лічбу по-різному: можна сказати, що тут 4 трійки коней, або 2 шестірки, або 12 коней. Така робота готує учнів до введення десятка як складеної лічильної одиниці.

Підсумовуючи слід зазначити, що, за методичною системою Л.П. Кочиної, основні питання нумерації розглядаються спочатку на відрізку чисел від 1 – го до 5–ти, а саме: називання чисел 1 – 5; лічба у межах 5–ти; утворення чисел з попереднього числа та одиниці; порівняння чисел; співвіднесення чисел до відповідної кількості предметів і навпаки; сприймання чисел на групах предметів; ознайомлення з цифрами, письмо цифр. Потім опрацьовуються зазначені питання на відрізку чисел від 6 –10. Письмо цифр дещо відстає від усної нумерації, тому на вивчення кожної цифри відводиться окремий урок.

За методичною системою М.В. Богдановича, основні питання нумерації розглядаються в межах конкретного числа, що вивчається.

Підсумовуючи слід зазначити, що детальне висвітлення методичних особливостей вивчення нумерації чисел першого десятка дозволить учителям початкової школи підготуватися до роботи відповідно вимог Державного стандарту початкової загальної освіти та нової базової навчальної програми для учнів початкової школи.

Дата добавления: 2014-11-18