Методика формування загального вміння розв’язувати задачі 4 страница

? ?

План розв’язування 1. Знаходимо спільну продуктивність дією додавання. 2. Знаходимо час спільної роботи дією ділення або продуктивність спільної праці дією множення, відповідаємо на запитання задачі.

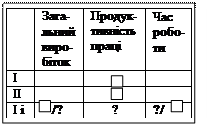
Істотні ознаки задач на спільну роботу (4- й клас): ці задачі містять три взаємопов’язані величини: загальний виробіток, продуктивність праці, час роботи; ці задачі містять три випадки: перший стосується роботи першого виконавця, другий – роботи другого виконавця, третій – спільної роботи двох виконавців; для двох випадків дано значення загального виробітку і часу роботи; для іншого випадку дано лише одне числове значення (або загального виробітку, або часу роботи), а інше – є шуканим.

Опорна схема, схематичний малюнок та план розв’язування таких задач подані в таблиці 7.

Дослідження задач на спільну роботу відбувається за наступними змінами: зміною ситуації задачі; зміною числових даних задачі; зміною шуканого задачі; за зміною „характеру дій” виконавців. Таке дослідження задачі є могутнім засобом визначення істотних ознак математичної структури та плану розв’язування задачі.

Таблиця 7

Опорні схеми та план розв’язування задач на спільну роботу, в яких шуканою є час спільної праці або загальний виробіток при спільній праці (4-й клас)

     

?

?

??

?

?

?

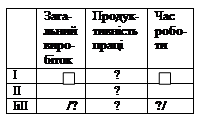
План розв’язування 1) знаходимо продуктивність першого виконавця дією ділення; 2) знаходимо продуктивність другого виконавця дією ділення; 3) знаходимо спільну продуктивність дією додавання; 4) знаходимо час спільної роботи дією ділення, або загальний виробіток при спільній праці дією множення; відповідаємо на запитання задачі.

2. Задачі на рух. Серед задач на рух виділяються дві групи: задачі на рух в різних напрямках (назустріч та у протилежних напрямках) та задачі на рух в одному напрямку (навздогін або з відставанням). У межах кожної групи задачі можна класифікувати за шуканою величиною: задачі на знаходження відстані, задачі на знаходження швидкості одного з рухомих тіл та задачі на знаходження часу руху. Наведемо приклади задач на рух у різних напрямках:

1) Два лижники вийшли одночасно назустріч один одному з двох селищ і зустрілися через 3 години. Перший лижник ішов зі швидкістю 12 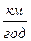, а інший – 14 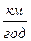. Яка відстань між селищами?

2) З двох сіл, відстань між якими 32 км, одночасно назустріч один одному вирушили трактор та бричка з конем і зустрілися через 2 години. Чому дорівнює швидкість трактора, якщо швидкість брички 7 ?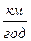

3) З Києва та Одеси одночасно назустріч один одному відправилися два автобуси. Швидкість першого автобуса 60 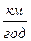, швидкість другого автобуса 90 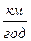. Через скільки годин вони зустрінуться, якщо відстань між містами 450 км?

Істотні ознаки задач на одночасний рух назустріч та в протилежних напрямках: в цих задачах йде мова про спільний рух двох тіл - 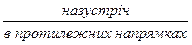;в цих задачах є чотири числові значення: швидкість руху першого тіла, швидкість руху другого тіла, час їх спільного руху, відстань, яку подолали обидва тіла під час спільного руху; при чому три з них дані, а одне – шукане.

t t

V₁ V₂ V₁ V₂

S S

План розв’язування (1 спосіб: S, V)

1) першою дією визначають відстань, яку подолало перше тіло.

2) другою дією визначають відстань, яку подолало друге тіло.

3) третьою дією відповідають на запитання задачі.

План розв’язування (2-й спосіб)

1) першою дією визначають на скільки 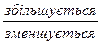відстань між тілами за одиницю часу.

2) другою дією відповідають на запитання задачі.

При формуванні в молодших школярів умінь розв’язувати задачі на рух доцільно паралельно розглядати задачі на одночасний рух назустріч і одночасний рух в протилежних напрямках, причому спочатку розв’язуються задачі на знаходження відстані і швидкості першим способом, а після засвоєння першого способу вводиться другий спосіб і вивчаються задачі на знаходження часу. Дослідження задач на одночасний рух відбувається за наступними змінами: за зміною напрямку руху тіл; за зміною числових даних задачі; за зміною шуканого. Визначення впливу цих змін на математичну структуру задачі та план її розв’язування допомагає учням сформулювати істотні ознаки задач на одночасний рух в різних напрямках та план їх розв’язування.

Серед додаткових питань чільне місце посідає узагальнення математичних структур та способів розв’язування задач на спільну роботу та на рух в різних напрямках. Якщо формулювання задачі на рух записати коротко в формі таблиці і порівняти із табличною формою короткого запису задачі на спільну роботу, то можна визначити схожість їх математичних структур, а тому наявність спільних істотних ознак:

			час
І		N1 / V1
ІІ		N2 / V2
І і ІІ	A / S		t

N₁ – продуктивність

праці першого

виконавця;

N₂ – продуктивність

праці другого виконав-

ця;

A – загальний виробіток при спільній праці; V₁ - швидкість першого тіла; V₂ - швидкість другого тіла; t – час спільного руху або час спільної праці; S – відстань між тілами на момент початку або на момент закінчення руху

Задачі на спільну роботу, в яких продуктивність спільної праці знаходять дією додавання, та задачі на одночасний рух в різних напрямках (назустріч та в протилежних напрямках) мають два способи розв’язання:

І спосіб	ІІ спосіб
А = N1 ∙ t + N2 ∙ t S = V1 ∙ t + V2 ∙ t	А = (N1 + N2) ∙ t S = (V1 + V2) ∙ t
	t = А: (N1 + N2) t = S: (V1 + V2)
N1 = (А - N2 ∙ t): t N2 = (А - N1 ∙ t): t V1 = (S - V2 ∙ t): t V2 = (S - V1 ∙ t): t	N1 = А: t - N2 N2 = А: t - N1 V1 = S: t - V2 V2 = S: t - V1

Таким чином, розглянуто загальні напрямки методики формування вмінь розв’язувати сюжетні математичні задачі. Результатом навчання математики в початковій школі має бути формування загального вміння розв’язувати сюжетні задачі (прості та складені на 2-4 дії, які є комбінаціями відомих видів простих задач), а також формування умінь розв’язувати задачі певних видів (задач на знаходження четвертого пропорційного, на пропорційне ділення, на знаходження невідомих за двома різницями, на подвійне зведення до одиниці, на спільну роботу, на рух). Досягнення цього результату можливе за умов теоретично обґрунтованої методичної системи навчання учнів початкової школи розв’язування сюжетних задач.

Дата добавления: 2014-11-18