Методика формування загального вміння розв’язувати задачі 3 страница

1) 2+3=5 (ваг.) всього привезли за два дні. 2) 95:5=19 (т) маса 1-го вагона. 3) 19∙2=38 (т) привезли першого дня. 4) 19∙3=57(т) привезли другого дня.  

Наведемо приклад задачі на пропорційне ділення. За два дні на базу привезли 95т вугілля. Першого дня привезли 2 вагони, а другого – 3 вагони. Скільки тонн вугілля привезли кожного дня, якщо маса 1-го вагона була однаковою?

	Загальна маса вугілля (т)	Маса 1-го вагона (т)	Кіль-кість вагонів (шт..)
І.	?		2 шт.
	95 т	?, однакова
ІІ.	?		3 шт.

Задача на знаходження невідомих за двома різницями. У кіоску продали по однаковій ціні 12 синіх та 8 чорних ручок. За сині ручки заплатили на 3 грн. 20 к. більше, ніж за чорні. Скільки грошей одержали за кожний вид ручок?

	Вартість (грн)	Ціна (грн)	1) 12 – 8 = 4 (шт.) – на стільки більше купили синіх ручок, ніж червоних; різниця між кількостями синіх та чорних ручок.   Кількість (шт..)
С.	?, на 320 к. б.		12 шт.
		?, однакова
Ч.	?		8 шт.

2) 320: 4 = 80 (к.) – ціна ручки.

3) 80 ^. 12 = 960 (к.) – вартість синіх ручок.

4) 80 ^. 8 = 640 (к.) – вартість чорних ручок.

Істотні ознаки задач на знаходження четвертого пропорційного, на пропорційне ділення та на знаходження невідомих за двома різницями: ці задачі містять три взаємопов’язані величини; ці задачі містять два випадки; одна з величин є однаковою для обох випадків; для однієї з величин дано

два числові значення для обох випадків; для другої величини Також можна узагальнити спосіб розв’язування задач на знаходження четвертого пропорційного, на пропорційне ділення та на знаходження невідомих за двома різницями способом знаходження однакової величини:

- знайти однакову величину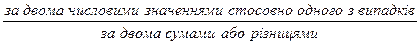

- відповісти на запитання задачі.

Методика навчання розв’язування задач на пропорційне ділення і на знаходження невідомих за двома різницями побудована за єдиним планом, в якому реалізовано наступні аспекти:

- для усвідомлення учнями зв’язку задач на знаходження четвертого пропорційного (на пропорційне ділення) і задач на пропорційне ділення (на знаходження невідомих за двома різницями) здійснюється перетворення задачі відомого виду в задачу нового виду;

- дослідження задачі реалізується шляхом: зміни величин або числових даних задачі, зміни шуканих, зміни однакової величини і визначення впливу цих змін на план розв’язування задачі.

Такий всебічний аналіз призводить до узагальнення істотних ознак задач цих видів і узагальнення плану їх розв’язування способом знаходження однакової величини.

Проілюструємо перетворення задачі одного виду у споріднений вид з метою визначення спільних ознак їх математичних структур та узагальнення способу розв’язування. Розглянемо задачу на знаходження четвертого пропорційного, яка розв’язується способом знаходження однакової величини.

Задача № 1. За 8 годин перший робітник виготовляє 88 деталей. Скільки деталей виготовить за 10 годин другий робітник, якщо працюватиме з тією самою продуктивністю?

Перед розв’язанням задачі робимо прикидку очікуваного результату: шукане число буде більшим за 88 деталей, тому що другий робітник працював більше часу при однаковій продуктивності. Учні „впізнають” задачу на знаходження четвертого пропорційного і актуалізують спосіб її розв’язування.

	Загальний виробіток	Продук- тивність праці	Розв'язання 1) 88: 8 = 11 (дет.) виготовляє робітник за 1 годину, однакова величина 2) 11 ∙ 10 = 110 (дет.) виготовить робітник за 10 годин Або: 88: 8 ∙10 = 110 (дет.) Відповідь: 110 деталей виготовить робітник за 10 годин роботи.   Час роботи
І	88 дет	однакова	8 год
ІІ	? дет		10 год

88

Після розв’язання цієї задач вчитель пропонує знайти сумарне значення загальної величини для двох випадків (загального виробітку: 88 + 110 = 198 (дет.)) і включити його в задачу, при

?

?

цьому змінити вимогу - знайти значення загальної величини для кожного з двох випадків.

Короткий запис задачі на знаходження четвертого пропорційного перетворюється у короткий запис нової задачі - на пропорційне ділення.

Задача № 2. Два робітники виготовили 198 деталей. Перший працював 8 годин, а другий – 10 годин. Скільки деталей окремо виготовив кожний робітник, якщо вони працювали з однаковою продуктивністю?

Учні роблять прикидку очікуваного результату: перший робітник зробить менше деталей, ніж другий, тому що він працював менше часу при тій самій продуктивності. Діти визначають зміни, що відбулися в попередній задачі, та їх вплив на розв’язування одержаної задачі. В задачі на знаходження четвертого пропорційного ми виконали наступні зміни: шуканими стали два числові значення однієї величини (загальної величини), але ми задали їх суму і одержали задачу на пропорційне ділення; при розв’язанні задач на пропорційне ділення ми не можемо однакову величину знаходити за двома відомими величинами одного з випадків, однакову величину ми знаходимо за двома сумами.

	Загальний виробіток	Продук- тивність праці	Розв’язання 1)8 + 10 = 18 (год) всього працювали робітники 2)198: 18 = 11 (дет.) продуктивність праці І або ІІ робітника, однакова величина 3)11 ∙ 8 = 88 (дет.) загальний виробіток І робітника 4)11 ∙ 10 = 110 (дет) загальний виробіток ІІ робітника Або: 198: (8 + 10) ∙ 8 = 88 (дет.) 198: (8 + 10) ∙ 10 = 110(дет.)     Час роботи
І	? 198д.	однакова	8 год
ІІ	?		10 год

1 98

??

8 10

?

Перевірка розв’язання здійснюється засобом додавання знайдених числових значень і порівняння отриманого числа з даним числовим значенням суми (88 + 110 = 198 (дет), що й дано за умовою задачі).

Учні порівнюють розглянуті два види задач і дістають висновку: обидві задачі містять три взаємопов’язані величини, два випадки, одна з величин є однаковою для обох випадків; для іншої величини дано два числові значення, а для третьої величини або дано одне числове значення, а друге є шуканим, або обидва числові значення є шуканими, але дано їх суму. Відмінність у математичних структурах впливає на спосіб знаходження однакової величини: в задачах на знаходження четвертого пропорційного її знаходять за двома числовими даними одного з випадків, а у задачах на пропорційне ділення – за двома сумарними значеннями двох інших величин.

Наступне дослідження задачі йде через введення в умову задачі не суми значень загальної величини, а їх різниці (одержуємо задачі на знаходження невідомих за двома різницями). Задача № 3. Перший робітник працював 8 годин, а другий 10 годин, причому другий робітник виготовив на 22 деталі більше, ніж перший. Скільки деталей зробив кожний робітник, якщо вони працювали з однаковою продуктивністю?

Розв’язання 1)10 – 8 = 2 (дет.) на стільки більше зробив другий робітник, ніж перший 2)22: 2 = 11 (дет.) продуктивність праці, однакова величина 3)11 ∙ 8 = 88 (дет.) загальний виробіток І робітника 4)11 ∙ 10 = 110 (дет) загальний виробіток ІІ робітника   Або: 22: (10 - 8) ∙ 8 = 88 (дет.) 22: (10 - 8) ∙ 10 = 110 (дет.)  

Розв’язання 1)10 – 8 = 2 (дет.) на стільки більше зробив другий робітник, ніж перший  

Перед розв’язанням задачі учні порівнюють одержану задачу з попередньою: ці задачі схожі тим, що обидві містять три взаємопов’язані величини, два випадки, одна з величин є однаковою для обох випадків; до однієї з них дано два числових значення, а обидва значення іншої величини є шуканими; відрізняються ці задачі тим, що в задачі на пропорційне ділення було дано значення суми загальних величин, а в цій – значення різниці. Отже, в обох задачах є однакова для двох випадків величина. У попередній задачі однакову величину знаходили за двома сумами, бо в умові було дано числове значення однієї з них, а в цій задачі дано значення різницевого відношення шуканих, тому однакову величину знаходитимемо за двома різницями. Таким чином, здійснена зміна умови задачі викликала застосування іншого способу знаходження однакової величини – за двома різницями.

	Загальний виробіток	Продук- тивність праці	Час роботи
І	?	однакова	8 год
ІІ	?, на 22 дет. біл.		10 год

? 22

?

?

Перевірка розв’язання здійснюється засобом знаходження різниці знайдених числових значень і порівняння одержаного числа з даним різницевим відношенням в умові задачі. Порівнюючи розв’язання задач на пропорційне ділення і на знаходження невідомих за двома різницями, діти встановлюють, що в обох задачах однакові дві останні дії, тому що в них одні й ті ж запитання та одна й та сама однакова величина, яка потрібна для відповіді на обидва запитання задачі. Розв’язки відрізняються першими двома діями, тому що однакову величину знаходили по-різному: у першій задачі – за двома сумами, а в другій задачі – за двома різницями (див. таблиця 4).

Таблиця 4

Опорні схема та плани розв’язування задач, що містять однакову величину (спосіб знаходження однакової величини)

Задачі на знаходження четвертого пропорційного  

Задачі на пропорційне ділення  

		... 1...
І	а		?
		Однак.
ІІ	с		?, на к б.(м.)

Задачі на знаходження невідомих за двома різницями

План розв’язування 1) Значення однакової величини – величини однієї одиниці - за двома числовими значеннями одного з випадків. 2) Шукане значення, відповідаємо на запитання задачі.  

План розв’язування 1) Суму даних числових значень однієї з величин. 2) Значення однакової величини – величини однієї одиниці - за сумарними значеннями двох величин. 3) Шукане значення, відповідаємо на перше запитання задачі. 4) Шукане значення, відповідаємо на друге запитання задачі.

План розв’язування 1) Різницю даних числових значень однієї з величин. 2) Значення однакової величини – величини однієї одиниці - за двома різницями. 3) Шукане значення, відповідаємо на перше запитання задачі. 4) Шукане значення, відповідаємо на друге запитання задачі.

До обов’язкових для всіх учнів питань не належать дослідження задач на пропорційне ділення та задач на знаходження невідомих за двома різницями засобом зміни однакової величини, а також порівняння задач на знаходження четвертого пропорційного, на пропорційне ділення і на знаходження невідомих за двома різницями з метою визначення спільних істотних ознак їх математичних структур та узагальнення способу розв’язування. Цей навчальний матеріал пропонується для поглибленого вивчення математики здібними та обдарованими учнями.

3. Аналогічним чином побудовано методику навчання молодших школярів розв’язування задач на подвійне зведення до одиниці, але з тією відмінністю, що дослідження задач цього виду не відбувається за допомогою зміни однакової величини.

Наведемо приклади задач на подвійне зведення до одиниці, що пропонуються в 3-му (1) та 4-му (2) класі:

  : 3 дні, 6 вів. – 36 кг   1день, 1 вів. -? кг

І спосіб 1) 36: 3 = 12 (кг) на 1 день 6-ти вівцям. 2) 12: 6 = 2 (кг) на 1 день 1-ій вівці. ІІ спосіб 1) 36: 6 = 6 (кг) на 3 дні 1-ій вівці. 2) 6: 3 = 2 (кг) на 1 день 1-ій вівці.  

1) На 3 дні 6-ти вівцям дають 36 кг сіна. Скільки сіна дають 1-ій вівці на день?

2) На 3 дні 6-ти вівцям дають 36 кг сіна. Скільки сіна дають 4-ом вівцям на день?

Для відповіді на запитання другої задачі треба виконати ще одну арифметичну дію: 3) 2 * 4 = 8 (кг) сіна дають 4-ом вівцям на 1 день.

Істотні ознаки задач на подвійне зведення до одиниці (3-й клас): чотири величини: кількість, час, загальне значення для даної кількості та часу, а також величина, яка поєднує усі ці величини – „подвійна одиниця”; дано три числові значення даних величин; шуканим є одне з числових значень: або величини подвійної одиниці, або загальної величини, або кількості, або часу.

План розв’язування (3-й клас)

1) першою дією знаходимо величину однієї одиниці для певної кількості або часу;

2) другою дією відповідаємо на запитання задачі.

Істотні ознаки задач на подвійне зведення до одиниці ( 4-й клас): чотири величини: кількість, час, загальне значення для даної кількості та часу, а також величина, яка поєднує усі ці величини – подвійна одиниця; два випадки; величина подвійної одиниці однакова для обох випадків; задача містить п’ять числових значень, при чому чотири дані за умовою задачі, а п’яте є шуканим.

Спосіб розв’язування задач на подвійне зведення до одиниці

( 4-й клас)

„Ключем” до розв’язання є знаходження значення величини „подвійної одиниці”.

Задачі на подвійне зведення до одиниці можна ввести (4-й клас) через ускладнення задачі на знаходження четвертого пропорційного. Наприклад:

Задача № 1 (задача на знаходження четвертого пропорційного). За 8 рейсів водій перевіз маршруткою 88 людей. Скільки людей він перевезе за 10 рейсів, якщо за один рейс він перевозить однакову кількість людей?

8 р. – 88 осіб

10 р. -? осіб

Записавши задачу на знаходження четвертого пропорційного схематично (у вигляді пропорції), діти зазначають, що „ключем” до розв’язання цієї задачі є знаходження однакової величини – величини однієї одиниці. Після розв’язання ускладнюємо задачу, увівши числове значення ще однієї величини (наприклад, в попередній задачі мова йшла про працю одного водія, а в ускладненій – про роботу двох водіїв). Зрозуміло, що в зв’язку з тим, що кількість водіїв збільшилася, збільшиться і значення загальної величини (кількості людей, що перевезли водії) у стільки разів, у скільки разів збільшилася кількість водіїв. У попередній задачі замінюють числове значення загальної величини в першому випадку на знайдене число. Запитання задачі лишаємо тим самим, але підкреслюємо, що запитується про одного водія.

Задача № 2 (задача на подвійне зведення до одиниці): Два водії за 8 рейсів перевезли маршруткою 176 людей. Скільки людей перевезе один водій за 10 рейсів?

Порівнявши отриману задачу з попередньою, діти встановлюють, що в них описується одна й та ж ситуація, є спільні величини, але в першій задачі мова йде тільки про одного водія, а у другій задачі – в першому випадку працюють два водії, а у другому лише один. Короткий запис задачі на знаходження четвертого пропорційного доповнюється відповідними числовими даними:

2 в., за 8 р. – 176 осіб

1 в., за 10 р. -? осіб

Можна виконати схематичний малюнок:

І спосіб: 1) 176: 2 = 88 (осіб) перевезе 1 водій за 8 рейсів; 2) 88: 8 = 11 (осіб) перевезе 1 водій за 1 рейс; 3) 11 ∙ 10 = 110 (осіб) перевезе 1 водій за 10 рейсів. Або: 176: 2: 8 ∙ 10 = 110 (осіб)  

176

??

1

?

Далі учні порівнюють розв’язання задачі на подвійне зведення до одиниці (І спосіб) та задачі на знаходження четвертого пропорційного і дістають висновку: задача на подвійне зведення до одиниці розв’язується трьома діями, тому що введено значення ще однієї величини, а задача на знаходження четвертого пропорційного – двома; причому обидва розв’язання містять дві однакові дії. Можна стверджувати, що, виконавши першу дію у розв’язанні задачі на подвійне зведення до одиниці, ми привели цю задачу до задачі на знаходження четвертого пропорційного. Спільним в обох задачах є наявність однакової величини – величини однієї одиниці в задачі на знаходження четвертого пропорційного і величини „подвійної одиниці” у задачі на подвійне зведення до одиниці. Спосіб розв’язування цих задач полягає в знаходженні значення величини однієї одиниці (зведення до одиниці) або значення величини „подвійної одиниці” (подвійне зведення до одиниці).

При розв’язанні і порівнянні одержаних задач учні приходять до аналогічних висновків (див. таблицю 5).

Таблиця 5

Опорні схеми та плани розв’язування задач на знаходження четвертого пропорційного та на подвійне зведення до одиниці

Задачі на знаходження четвертого пропорційного

–   -?

Задачі на подвійне зведення до одиниці

?

?

?? 1,1 ?

План розв’язування Спосіб знаходження однакової величини 1) Значення однакової величини – величини однієї одиниці за двома числовими значеннями одного з випадків. 2) Шукане значення загальної величини, відповідаємо на запитання задачі.

План розв’язування 1) знаходимо величину однієї одиниці для даної кількості або часу; 2) знаходимо величину „подвійної одиниці”; 3) відповідаємо на запитання задачі.  

Аналогічно розглянутим видам задач побудовано методику навчання молодших школярів розв’язування задач на подвійне зведення до одиниці, з тією лише відмінністю, що дослідження задач цього виду не відбувається за допомогою зміни однакової величини. У результаті зміни величин задачі або числових даних, або зміни шуканого діти узагальнюють математичні структури та план розв’язування задач на подвійне зведення до одиниці.

ІІ. Програма вивчення задач на процеси та методика навчання розв’язування задач цього типу реалізується в 3-х – 4-х класах. Відповідно до чинної програми спочатку відбувається навчання молодших школярів розв’язування задач на спільну роботу, а потім – на одночасний рух.

1. Формування в учнів уміння розв’язувати задачі на спільну роботу здійснюється в 3-му та 4-му класах, що пояснюється дещо відмінними математичними структурами задач цього виду: так, у 3-му класі пропонуються задачі на спільну роботу, в яких дано продуктивність кожного виконавця, а у 4-му – не дано продуктивності кожного виконавця, вона є проміжним невідомим.

Наприклад (3-й клас). Одна друкарка друкує за годину 5 сторінок, інша 4. Скільки годин вони повинні працювати разом, щоб надрукувати 72 сторінки?

Істотні ознаки задач на спільну роботу (3-й клас): ці задачі містять три взаємопов’язані величини: загальний виробіток, продуктивність праці, час роботи;ці задачі містять три випадки: перший стосується роботи першого виконавця, другий – роботи другого виконавця, а третій – спільної роботи двох виконавців;дано продуктивність кожного виконавця, а шуканим є

або дано

загальний виробіток та час при спільній роботі, а шуканим є продуктивність праці одного з виконавців.

Опорна схема, схематичний малюнок та план розв’язування таких задач подані у таблиці 6.

Наприклад (4-й клас). Одна друкарка друкує за 6 годин 30 сторінок тексту, інша за 4 години 16 сторінок. Скільки годин вони повинні працювати разом, щоб надрукувати 72 сторінки тексту?

Таблиця 6

Опорні схеми та план розв’язування задач на спільну роботу, в яких шуканою є час спільної праці або загальний виробіток при спільній праці

Дата добавления: 2014-11-18