
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Класифікація простих задач 1 страница
|
|
|
|
| № | Тип задачі | Вид задачі | Схематичний рисунок | ||||||||||||
| Співвідно-шення додавання Слова-ознаки співвідно-шення „всього” або його синоніми (або „було” – „стало”). Головний член співвідно-шення А той, в опис якого входить слово-ознака „всього” або „стало” (це ціле). Головний член дорівнює сумі інших членів співвідно-шення. Інші члени знаходять за правилом знаходження невідомого компонента. | 1. Задачі на знаходження суми двох доданків 1 ) У Наталки 7 зошитів у лінійку та 3 зошити у клітинку. Скільки всього зошитів в Наталки? 2) У Наталки було 4 зошити, мама їй купила 5 зошитів. Скільки зошитів стало в Наталки? 2. Задачі на знаходження невідомого доданка 1 ) У Наталки всього 10 зошитів, з них 7 зошитів у лінійку. Скільки зошитів у клітинку в Наталки? 2) У Наталки було 4 зошити, після того як мама їй купила кілька зошитів, в неї стало 9 зошитів. Скільки зошитів купила мама? 3. Задачі на знаходження суми трьох доданків В Іринки 3 зошити, у Сашка 2 зошита, в Миколи 4 зошити. Скільки всього зошитів у дітей? 4. Задачі на знаходження третього числа за сумою двох даних чисел В Іринки 3 зошити, у Сашка 2 зошити, а в Миколи стільки зошитів, скільки в Сашка та Іринки разом. Скільки зошитів у Миколи? | К В
?
А
?
? | |||||||||||||
| Співвідно-шення віднімання Слова-ознаки співвідно-шення „було” - „за-лишилося”. Головним членом А є той, в опис якого входить слово-ознака „залишило-ся”, він є різницею двох інших членів співвідно-шення К і В, де К той член, в опис якого входить слово-ознака „було”. | 1. Задачі на знаходження остачі. В Наталки було 7 зошитів, вона витратила 3 зошити. Скільки зошитів залишилося в Наталки? 2. Задачі на знаходження невідомого зменшуваного. Після того, як Наталка витратила 3 зошити, в неї залишилося 4 зошити. Скільки зошитів було в Наталки? 3. Задачі на знаходження невідомого від’ємника. У Наталки було 7 зошитів, після того, як вона витратила кілька зошитів, у неї залишилося 4 зошити. Скільки зошитів витратила Наталка? |  К К
В?
В А
? А
| |||||||||||||
| Співвідно-шення різницевого порівняння Слова-ознаки співвідно-шення „ на... менше (більше)”. Головний член співвідно-шення А той, в описі якого стоїть слово-ознака – прийменник „на”, цей член є різницею двох значень К і В однієї й тієї самої величини, що порівнюються, де К > В. | 1. Задачі на різницеве порівняння. У Наталки 6 зошитів у клітинку та 4 зошити в лінійку. На скільки більше зошитів у клітинку, ніж у лінійку в Наталки? На скільки меншезошитів у лінійку, ніж у клітинку? 2. Задачі на збільшення або зменшення числа на кілька одиниць. У Наталки 4 зошити в лінійку, а в клітинку на 2 зошити більше. Скільки зошитів у клітинку в Наталки? У Наталки 6 зошитів у клітинку, а в лінійку на 2 зошити менше. Скільки зошитів у лінійку в Наталки? | В

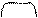 ? ?
 К
В
К
В

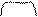 Стільки ж та А Стільки ж та А
 ?
?
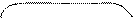 Б Б
 Стільки ж без А
Стільки ж без А
 ?
?
| |||||||||||||
| Співвідно-шення переходу від більшої одиниці лічби або вимірюван-ня до меншої. Ознакою цього виду співвідно-шення є те, що один і той самий об’єкт перерахова-ний або виміряний двома різними одиницями (мірками) – більшою і меншою і вказано, що кожна більша одиниця містить по В дрібних одиниць. Головним членом А співвідно-шення є результат лічби або вимірюван-ня об’єкта дрібними одиницями. | 1. Задачі на конкретний зміст добутку. Скільки олівців у 3 коробках, якщо в кожній по6 олівців? |
В
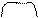         ... ...
 К разів
? К разів
?
| |||||||||||||
| Співвідно-шення розбиття цілого на рівні частини. Ознакою цього виду співвідно-шення є те, що К розбито на А рівних частин, в кожній з яких „по” В одиниць. Головним членом співвідно-шення є А – результат розбиття К на частини по В одиниць в кожній. | 1. Задачі на конкретний зміст дії ділення: - ділення на рівні частини; Риску довжиною 15 дм розрізали на 5 рівних частин. Яка довжина кожної частини? - ділення на вміщення. Риску довжиною 15 дм розрізали по 3 дм. Скільки одержали таких частин? | К
        ...
А разів
?
або ...
А разів
?
або
  К
? К
?
 А
К
А
К
        ...
? разів
В
Або ...
? разів
В
Або
  К
В К
В
 ?
?
| |||||||||||||
| Співвідно-шення кратного порівняння Слова-ознаки співвідно-шення „ у...більше (менше)”, Головний член А співвідно-шення той, в опис якого входить вираз „разів”, він є результатом кратного порівняння (відношен-ня) двох значень К і В однієї й тієї самої величини, при чому К > В. | 1. Задачі на кратне порівняння. В Іринки 8 зошитів у клітинку і 4 зошити в лінійку. У скільки разів більше зошитів у клітинку, ніж у лінійку в Іринки? У Скільки разів менше зошитів у лінійку, ніж у клітинку? 2. Задачі на збільшення або зменшення числа в кілька разів. В Іринки 4 зошити в лінійку, а в клітинку в 2 рази більше. Скільки зошитів у клітинку в Іринки? В Іринки 8 зошитів у клітинку, а в лінійку в 2 рази менше. Скільки зошитів у лінійку в Іринки? | К
         ... ...
  скільки разів?
В
Або скільки разів?
В
Або
  К
В К
В
 ?
В
?
В
   у А разів більше у А разів більше
    ...
?
або ...
?
або
  ?
В ?
В
 А
А
| |||||||||||||
| Співвідно-шення частин і цілого Слова-ознаки співвідно-шення: „складає... частину... від”. Головний член А співвідно-шення той, у завдання якого входить слово-ознака „частина”, він є результатом ділення членів К і В на значення однієї і тієї самої величини, при цьому К<В. | 1. Задачі на знаходження частини від числа.
Тато посадив 12 дерев, а Сашко 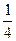 від того, що посадив тато. Скільки дерев посадив Сашко?
2. Задачі на знаходження числа за його частиною.
Сашко посадив 3 дерева, що складає від того, що посадив тато. Скільки дерев посадив Сашко?
2. Задачі на знаходження числа за його частиною.
Сашко посадив 3 дерева, що складає 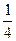 від того, що посадив тато. Скільки дерев посадив тато?
3. Задачі на знаходження дробу, який одне число становить від іншого.
Тато посадив 12 дерев, а Сашко 3. Яку частину дерев посадив Сашко відтих дерев, що посадив тато? від того, що посадив тато. Скільки дерев посадив тато?
3. Задачі на знаходження дробу, який одне число становить від іншого.
Тато посадив 12 дерев, а Сашко 3. Яку частину дерев посадив Сашко відтих дерев, що посадив тато?
| Б
        ...
А частин
?
або ...
А частин
?
або
 1 - Б 1 - Б

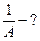 ?
?
   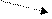 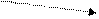    ...
А частин
В
або ...
А частин
В
або
 1 -? 1 -?

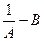 К
К
В | |||||||||||||
| Співвідно-шення -залежність між значеннями різних величин. Ознака співвідно-шення – явне завдання в умові задачі двох різних величин, які, як відомо, пов’язані якоюсь функціона-льною залежністю. Головним членом А цього співвідно-шення є загальна величина | 1. Задачі на знаходження значення загальної величини (вартості, загальної довжини, загального об’єму, загальної маси, загального виробітку, відстані, площі прямокутника тощо) Скільки всього кілограмів помідорів у 3-х ящиках, якщо в кожному ящику по 8 кг помідорів? 2. Задачі на знаходження величини однієї одиниці лічби або вимірювання (ціни, довжини 1-го відрізка, об’єму 1-ої посудини, маси 1-го предмету, продуктивності праці, швидкості тощо) В 3 ящиках 24 кг помідорів. Скільки кілограмів помідорів у одному такому ящику? 3. Задачі на знаходження кількості (куплених речей, відрізків, посудин, предметів) або часу (роботи, руху). У ларьок привезли 24 кг помідорів у ящиках по 8 кг у кожному. Скільки ящиків з помідорами привезли в ларьок? |
 ?
К ?
К
       ...
В ...
В
 А
? А
?
  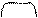     ...
В ...
В
 А
К А
К
  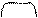     ...
? ...
?
|
Подані види задач пропонуються протягом чотирьох перших років навчання. Природно, що найбільша кількість нових видів простих задач припадає на перші два роки навчання. У подальшому навчанні береться до уваги, що вміння розв’язувати прості задачі вже сформовано і на перший план виступає формування вміння розв’язувати складені задачі.
Під складеною задачею розуміють таку задачу, на запитання якої не можна відповісти відразу, виконавши одну арифметичну дію; для розв’язання складеної задачі треба виконати дві і більше арифметичні дії.
Для класифікації складених задач немає єдиної основи, тому їх можна поділити на дві групи. До першої групи відносяться складені задачі, які містять різноманітні поєднання відомих видів простих задач, крім співвідношення залежності між значеннями різних величин. Ці задачі можна записати коротко схематично, причому на цьому короткому записі майже завжди можна виділити складові прості задачі.
До другої групи відносяться задачі, в яких явища, що описуються, характеризуються кількома взаємопов’язаними величинами, тобто містять співвідношення залежності між значеннями різних величин. Короткий запис таких задач доцільніше подавати у формі таблиці.
Складені задачі першої групи можна класифікувати за назвою простої задачі, що має розв’язуватися останньою. Отже, існують такі види складених задач: задачі на знаходження остачі (різниці); задачі на знаходження суми; задачі на знаходження невідомого доданка; задачі на знаходження невідомого зменшуваного; задачі на знаходження невідомого від’ємника; задачі на збільшення або зменшення числа на кілька одиниць; задачі на різницеве порівняння; задачі на знаходження добутку; задачі на знаходження частки; задачі на збільшення або зменшення числа в кілька разів; задачі на кратне порівняння; задачі на знаходження дробу від числа; задачі на знаходження числа за його дробом.
Другу групу складених задач (задачі, що містять пропорційні величини) доцільно розділити на дві підгрупи:
1) задачі, що містять знаходження суми, різницеве чи кратне порівняння: на знаходження суми двох добутків (часток); задачі, обернені до задач на знаходження суми двох добутків (часток); на різницеве порівняння двох добутків (часток); задачі, обернені до задач на різницеве порівняння двох добутків (часток); задачі на кратне порівняння двох добутків (часток); задачі, обернені до задач на кратне порівняння двох добутків (часток); задачі, які містять різницеве (кратне) відношення;
2) „типові” задачі:
- задачі, що містять однакову (сталу) величину (задачі на знаходження четвертого пропорційного, задачі на пропорційне ділення, задачі на знаходження невідомих за двома різницями, задачі на подвійне зведення до одиниці);
- задачі на процеси (задачі на спільну роботу, задачі на рух).
Розв’язування задачі є складним процесом розумової діяльності людини, який спрямований на перетворення об’єкта, що описаний у змісті задачі, на вирішення суперечності між умовою та вимогою задачі. Здебільшого методисти визначають чотири етапи процесу розв’язування як простої, так і складеної сюжетної задачі:
1) ознайомлення з задачею, аналіз тексту задачі;
2) пошук розв’язування задачі;
3) реалізація плану розв’язування задачі; запис розв’язання і відповіді;
4) робота над задачею після її розв’язання.
Діяльність з розв’язування задач може здійснюватися як алгоритмічним, так і евристичним способом. Якщо учень виконує приписи, то в цьому випадку здійснюється алгоритмічний спосіб діяльності з розв’язування задач, який характеризується тим, що учень здійснює власну діяльність у відповідності з відомим йому алгоритмом.Якщо, розпочинаючи розв’язання математичної задачі, учень не має орієнтувальної основи для своїх дій, то він її відшукує, виконуючи евристичну діяльність. Така діяльність здійснюється за допомогою особливих прийомів – евристик.
Вченими доведено, що домінуючою евристикою при розв’язуванні задач є моделювання як задачної ситуації (побудову допоміжних моделей – предметних, схематичних, словесних), так і процесу її розв’язування (схеми аналітичного і синтетичного розбору задачі, „дерева міркувань”), тому що саме воно забезпечує необхідне орієнтування в задачній ситуації.
Незалежно від способу (алгоритмічного чи евристичного) діяльність учнів із розв’язування задач являє собою реалізацію основних етапів щодо виконання певних дій. Перш ніж розглядати дії, за допомогою яких реалізуються етапи розв’язування задачі, необхідно акцентувати увагу на правильному розумінні таких висловлювань:
розв'язати задачу — означає встановити (розкрити, відшукати, побачити, пояснити) зв'язки між даними і шуканим числами, на основі чого дібрати потрібні арифметичні дії та їх порядок виконання, знайти результати дій, а потім відповісти на запитання задачі. Відповідь задачі не відгадується, а знаходиться при виконанні потрібних дій (операцій). Для знаходження шуканого числа треба вміти пояснити (розказати), які дії і над якими числами варто виконати, в якому порядку і чому саме такі відповіді на запитання задачі;
розв'язування задачі – це процес, робота, яка включає ознайомлення з текстом задачі, роздуми (міркування) над її розв'язанням, запис чи формулювання дій та відповідей.
розв'язання задачі – це запис (формулювання) порядку арифметичних дій, за допомогою яких знаходиться відповідь до задачі.
розв'язок – відповідь на запитання задачі (а ще розв'язком називають числове значення шуканої величини).
1.Ознайомлення з задачею. Аналіз тексту задачі.
Ознайомитися – це означає, прочитавши формулювання задачі, уявити собі життєву ситуацію, яка відображена в ній. Проаналізувати текст задачі – це означає виділити умову і запитання; визначити величини, що входять до задачі (дані та шукані), встановити зв’язки між ними.
Наприклад:
1.Біля ставка росло 9 верб, 2 осики, а вільх стільки, скільки верб і осик разом. Скільки вільх росло біля ставка?
І. Ознайомлення з умовою задачі. Аналіз умови.
- Прочитай задачу та уяви, про що в ній розповідається. Про що розповідається в задачі? (У задачі розповідається про верби, осики та вільхи. Росло 9 верб, 2 осики, а вільх стільки, скільки верб і осик разом. Запитується: скільки росло вільх?)
- Розкажи задачу. Розкажи умову. Розкажи запитання. Виділи числові дані. Що вони означають? (Число 9 означає, що росло 9 верб; число 2 означає, що росло 2 осики.) Яке число є шуканим? (Шуканим є число вільх.)
- Виділи ключові слова та склади короткий запис задачі. (Ключові слова: верби, осики, вільхи.) Чи відомо нам, скільки росло верб? (Відомо – 9) Запишемо це поряд з словом “Верби”. Чи знаємо ми із умови, скільки росло осик? (Знаємо – 2) Запишемо це поряд з словом “Осики”. Чи відомо, скільки було вільх? (Ні, невідомо.) А що нам відомо із умови задачі про вільхи? (Вільх було стільки, скільки верб і осик разом.) Як це позначимо в короткому запису? (Якщо говориться “разом”, то це позначаємо фігурною дужкою, тобто те, що стосується верб і осик слід об'єднати фігурною дужкою і посередині записати, що це число дорівнює числу вільх). Тому короткий запис буде такий:
 Верби – 9 шт.
Верби – 9 шт.
Вільхи –?
Осики – 2 шт.
- За коротким записом поясни числові дані задачі та запитання. Що позначає число 9? (Число 9 позначає, скільки росло верб.) Що позначає число 2? (Число 2 позначає, скільки росло осик.) Що позначає фігурна дужка і поряд слово „вільхи”? (Фігурна дужка позначає, що вільх стільки, скільки верб і осик разом.) Яке запитання задачі?(Скільки росло вільх?)
- Яким співвідношенням пов’язані числа в задачі? (В задачі є слово-ознака „всього”, тому тут задано співвідношення об’єднання частин у ціле – співвідношення додавання. Проміжним невідомим є сума, яку знаходять дією додавання. Крім того, вільх стільки, скільки верб і осик разом, тому тут є ще співвідношення рівності.)
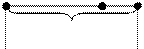
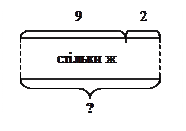 Зробимо схематичний малюнок. Скільки верб росло біля ставка? Як показати, що біля ставка росло 9 верб? Скільки осик росло? Як це показати: треба об'єднувати чи виключати? Скільки вільх росло біля ставка? (Стільки ж, скільки верб і осик разом.) Як це показати на схемі? (Треба нижче накреслити відрізок такої ж довжини, що й відрізок, який показує скільки верб і осик разом.)
Зробимо схематичний малюнок. Скільки верб росло біля ставка? Як показати, що біля ставка росло 9 верб? Скільки осик росло? Як це показати: треба об'єднувати чи виключати? Скільки вільх росло біля ставка? (Стільки ж, скільки верб і осик разом.) Як це показати на схемі? (Треба нижче накреслити відрізок такої ж довжини, що й відрізок, який показує скільки верб і осик разом.)
ІІ. Пошук розв’язування задачі
Пошук розв’язування задачі арифметичним способом може здійснюватися від запитання задачі до числових даних, тобто аналітично, або від числових даних задачі до її запитання – синтетично.
У практиці навчання застосовуються обидва шляхи, але переваги належать синтетичному методу, оскільки аналітичний у чистому вигляді більш складний для учнів. Синтетичний метод для дітей простіший, але застосування його може створювати додаткові проблеми; аналітичний - більш цілеспрямований щодо складання плану розв'язування задачі, тут треба мати на увазі не одну якусь дію, а хід міркування в цілому.
С.Є. Царьова розглядає пошук розв’язування задачі не лише як міркування „від запитання задачі до числових даних” або „від числових даних до запитання”, а й як знаходження різних шляхів розв’язування задачі: пошук за предметною або графічною моделлю (цей спосіб реалізується в системі розвивального навчання Д.Б. Ельконіна та В.В. Давидова), пошук за допомогою відокремлення словесного завдання математичних відношень і перекладу їх на мову виразів (створення структурних моделей за Л.М. Фрідманом).
Для складених задач пошук розв’язування задачі завершується складанням плану розв’язування, в якому обговорюється, про що треба дізнатися першою дією, другою дією, і так далі…
Бесіда, наприклад, матиме такий зміст.
- Повтори запитання задачі. Що потрібно знати, щоб на нього відповісти? (Потрібно знати: І – що вільх було стільки, скільки верб і осик разом, та ІІ – скільки верб і осик разом (поки не знаємо).) Тут дія не виконується, але здійснюється логічний перехід до запитання “Скільки верб і осик разом?” Що потрібно знати, щоб на нього відповісти? (Потрібно знати два числових значення: І – скільки верб (9) та ІІ – скільки осик (2).)
|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 1421; Нарушение авторских прав?; Мы поможем в написании вашей работы!


 К?
К?

 К В С
К В С



 ?
?