Основные свойства временных булевых функций

По результатам предыдущего параграфа любая временная булева функция может быть представлена в виде

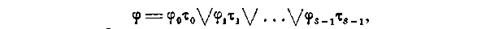
где φ_i (i = 0, 1,..., s-1) есть функции алгебры логики. Любая функция алгебры логики может быть представлена либо в дизъюнктивной, либо в конъюнктивной совершенной нормальной формах. дадим следующие два определения.

Определение. Если во временной булевой функции все функции φ_i (i = 0, 1,..., s-1) представлены в ДСНФ, то соответствующее выражение для φ называется дизъюнктивной совершенной нормальной формой временной булевой функции φ.

Если во временной булевой функции все функции φ_i (i = 0, 1,..., s-1) представлены в КСНФ, то соответствующее выражение для φ называется конъюнктивной совершенной нормальной формой временной булевой функции φ.

Из этих определений и соответствующих теорем для функций алгебры логики вытекает следующая теорема.

Теорема. Любая временная булева функция может быть представлена в ДСНФ или КСНФ.

Пример 4.4. Записать в ДСНФ и КСНФ следующую временную булеву функцию.

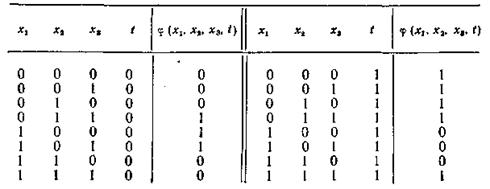
Составляем ДСНФ и КСНФ для φ₀ и φ₁:

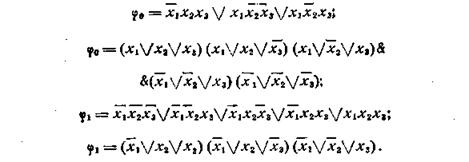
После этого пишем ДСНФ и КСНФ данной временной булевой функции φ:

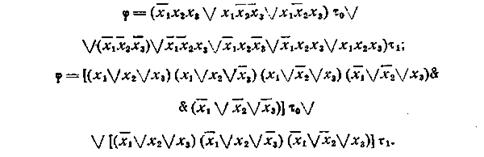
В силу вышесказанного ясно, что задача минимизации временных булевых функций может быть решена с помощью средств, подобных тем, какие рассматривались для случая минимизации функций алгебры логики.

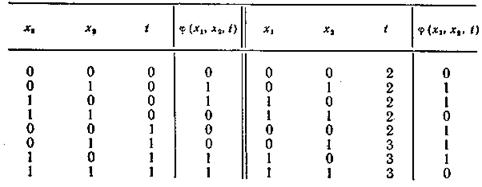
Пример 4.5. Рассмотрим следующую функцию φ (х₁, x₂, t).

Согласно определению, получим ДСНФ этой функции:

Составим теперь минимизационную карту по методу неопределенных коэффициентов для φ, основываясь на принципе составления таких карт для функций алгебры логики, рассмотренном в гл. 1, и применим эту карту для минимизации данной функции φ.

Согласно этой минимизационной карте, МДНФ функции φ имеет вид:

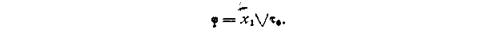
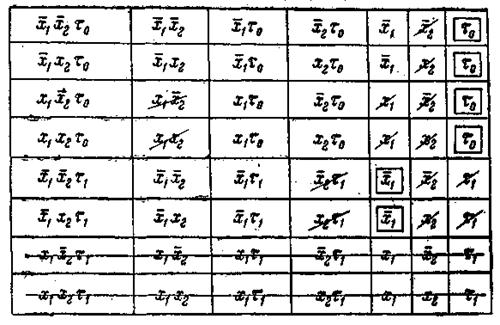
Рисунок 4.1 - Минимизационная карта к примеру 4.5

Пример 4.6. Применим теперь метод неопределенных коэффициентов для функции, рассмотренной в примере 4-4. Соответствующая МДНФ получена на основании минимизационной карты, приведенной на рисунке 4.2, и имеет вид:

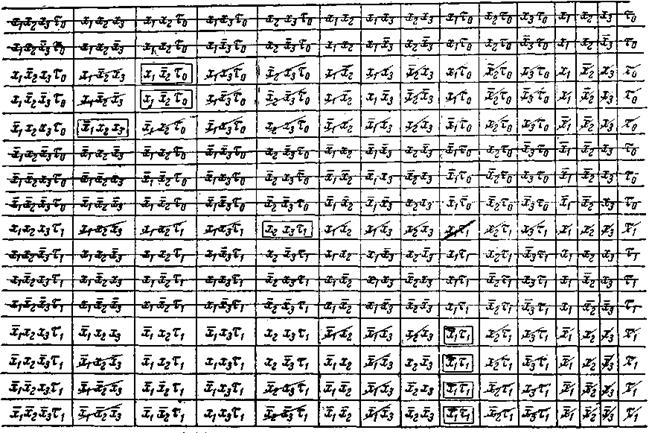
Рисунок 4.2 - Минимизационная карта к примеру 4.6

Из приведенных примеров видно, что минимизационные карты в случае временных булевых функций достаточно громоздки и работа с ними при числе переменных х более трех или при большом количестве допустимых значений t затруднительна. В подобных случаях можно проводить неполную минимизацию. Неполная минимизация проводится следующим образом. Пусть ДСНФ временной булевой функции φ имеет вид:

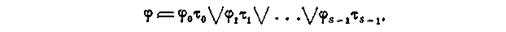
Находим по обычным правилам МДНФ для φ₀, φ₁, φ₂,.., φ_s-1 и за приближенное минимальное выражение для φ берем:

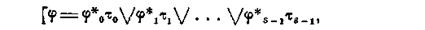
где 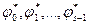- МДНФ функции φ_i (i =0,1,...,s-1). При большом (s-1) и малом количестве аргументов х в функциях φ_i такой метод достаточно продуктивен.

Пример 4.7. Применяя метод неполной минимизации для функции примера 4.5, получим:

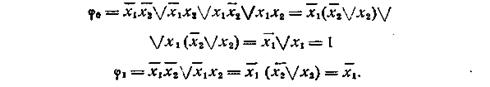
За неполную минимальную форму ВБФ принимаем выражение

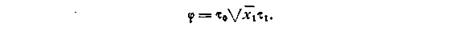
Пример 4.8. Теперь применим метод неполной минимизации

для временной булевой функции примера 4.4:

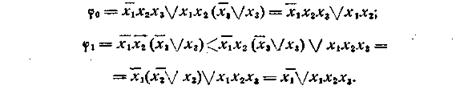
Неполная минимальная форма для φ запишется в виде следующего выражения:

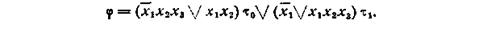
Пример 4.9. Найдем неполную минимальную форму для следующей временной булевой функции:

Выписываем ДСНФ для функций φ₀, φ₁, φ₂, φ₃;

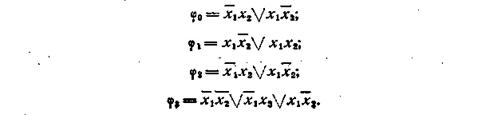
После минимизации каждой из этих функций получим

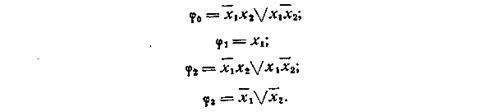
В результате получаем минимальную форму для φ:

Применим теперь для функции φ метод минимизирующих карт:

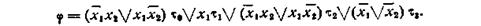
Таким образом, в этом случае приближенная минимальная форма оказалась МДНФ для данной функции. Для минимизации временных булевых функций, кроме метода минимизирующих карт, можно применять любые методы минимизации, рассмотренные для функций алгебры логики.

Дата добавления: 2014-11-18