Описание интегральной математической модели пожара в помещении

Интегральная модель пожара позволяет получить информацию, т.е. сделать прогноз, о средних значениях параметров состояния среды в помещении для любого момента развития пожара. При этом для того, чтобы сопоставлять средние (т.е. среднеобъемные) параметры среды с их предельными значениями в рабочей зоне, используются формулы, полученные на основе экспериментальных исследований пространственного распределения температур, концентраций продуктов горения, оптической плотности дыма и т.д.

Газовая среда, заполняющая помещение с проемами (окна, двери и т.п.), как объект исследования есть открытая термодинамическая система.

Эта система взаимодействует с внешней средой путем тепло - и массообмена. Будем считать, что в начальной стадии процесса развития пожара через одни проемы выталкиваются из помещения нагретые газы, а через другие поступает холодный воздух (рис. 1.1). Количество вещества в рассматриваемой открытой термодинамической системе в течение времени изменяется. Термодинамическая система совершает работу, выталкивая нагретые газы во внешнюю атмосферу. Поступление холодного воздуха обусловлено работой проникновения, которую совершает внешняя среда. Эта термодинамическая система взаимодействует также с ограждающими конструкциями путем теплообмена. Кроме того, в эту систему с поверхности горящего материала поступает вещество в виде газообразных продуктов горения. Состояние рассматриваемой термодинамической системы изменяется в результате взаимодействия с окружающей средой. В интегральном методе описания процесса изменения состояния рассматриваемой термодинамической системы, сделаны два допущения.

Рис. 1.1. Схема интегральной модели пожара в помещении

Во-первых, всегда с большой точностью можно считать, что газовая среда внутри помещения при пожаре есть смесь идеальных газов.

Во-вторых, в каждой точке пространства внутри помещения в любой момент времени реализуется локальное равновесие. Это означает, что локальные значения основных термодинамических параметров состояния (плотность, давление, температура) связаны между собой уравнением Клапейрона, т.е.

P = rRT,

P -локальное давление, Н·м²;

r - локальная плотность, кг·м^-3;

R -удельная газовая постоянная, Дж·(кг·К)^-1;

Т -локальная температура, К.

Будем считать, что во время пожара поля локальных термодинамических параметров состояния являются нестационарными и неоднородными. Расчет этих полей представляет собой чрезвычайно сложную математическую задачу. Интегральный метод описания состояния среды в помещении позволяет не рассматривать эту задачу.

В интегральном методе описания состояния термодинамической системы, коей является газовая среда в помещении, используются «интегральные» параметры состояния - такие, как масса всей газовой среды и ее внутренняя тепловая энергия. Отношение этих двух интегральных параметров позволяет оценивать в среднем степень нагретости газовой среды. В процессе развития пожара значения, указанных интегральных параметров состояния, изменяются.

Особенностью рассматриваемой термодинамической системы (т.е. газовой среды в помещении) является то, что ее объем (т.е. пространственная конфигурация) в процессе развития пожара практически не изменяется. В связи с этим вместо вышеуказанных интегральных параметров состояния целесообразно использовать при исследовании процесса изменения состояния термодинамической системы среднеобъемные параметры - среднеобъемную плотность газовой среды и среднеобъемную (удельную) внутреннюю энергию.

Среднеобъемная плотность газовой среды в помещении представляет собой отношение массы газа, заполняющего помещение, к объему помещения, т.е.

P_m = M / V,

М - масса газа, заполняющего помещение, кг;

V - свободный объем помещения, м³;

Следует отметить, что

M = .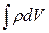

С формальных позиций среднеобъемная внутренняя энергия газовой среды есть результат осреднения по объему всех значений локальной плотности, т.е.

.

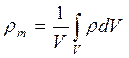Газовая среда в помещении представляет собой смесь кислорода, азота и продуктов горения. В процессе развития пожара количественное соотношение между компонентами смеси изменяется. В интегральном методе описания процесса изменения массы i -гокомпонента смеси в течение времени используется параметр, называемый среднеобъемной парциальной плотностью i -го компонента смеси.

Среднеобъемная парциальная плотность i -гокомпонента представляет собой отношение массы i-го компонента смеси (например О₂), содержащейся в объеме помещения, к объему помещения, т.е.

,

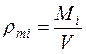M, - масса i -го компонента, находящегося в помещении, кг.

Отметим, что с формальной точки зрения среднеобъемная парциальная плотность i-го компонента есть результат осреднения по объему помещения всех значений локальной парциальной плотности этого компонента, т.е.

,

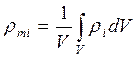ρ, - локальное значение парциальной плотности i -го компонента, кг·м^-3.

Среднеобъемная (удельная) внутренняя энергия представляет собой отношение внутренней тепловой энергии всего газа, заполняющего помещение, к объему помещения, т.е.

,

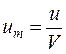u – внутренняя энергия всей газовой среды, заполняющей помещение.

С формальных позиций среднеобъемная внутренняя энергия газовой среды есть результат осреднения по объему всех значений локальной удельной (объемной) внутренней энергии, т.е.

.

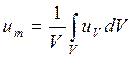Локальные значения удельной объемной внутренней энергии и удельной массовой внутренней энергии связаны между собой простым соотношением, которое имеет следующий вид:

,

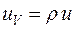u - локальное значение удельной массовой внутренней энергии газа, Дж·кг^-1.

Отметим здесь, что между локальным значением удельной массовой внутренней энергии и локальной температурой идеального газа существует простая взаимосвязь, а именно

,

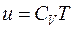C_V - изохорная теплоемкость газа, Дж·кг^-1·К^-1.

В интегральном методе описания процесса изменения состояния термодинамической системы (т.е. газовой среды в помещении) вместо среднеобъемной внутренней энергии используется параметр состояния, называемый среднеобъемным давлением. Эти два параметра в формальном отношении являются взаимозаменяемыми. Формулу можно преобразовать с помощью выражений

.

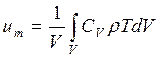Если теперь воспользоваться уравнением Клапейрона, то можно преобразовать и получить следующее выражение:

,

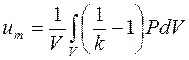P - локальное давление, Н·м^-2;

k - отношение изобарной и изохорной теплоемкостей идеального газа (показатель адиабаты).

С достаточной для практики точностью можно считать, что показатель адиабаты во всех точках внутри помещения есть одна и та же постоянная величина. С учетом этого замечания формулу можно преобразовать:

.

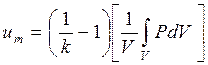Выражение в прямоугольных скобках представляет собой операцию осреднения всех локальных значений давления по объему помещения. Результат этого осреднения называют среднеобъемным давлением, т.е.

,

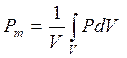P_m - среднеобъемное давление, Н·м^-2.

Сравнивая выражения, получим следующее соотношение между среднеобъемной внутренней энергией и среднеобъемным давлением:

.

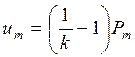Из последней формулы следует, что среднеобъемное давление прямо пропорционально среднеобъемной внутренней энергии. Среднеобъемное давление необходимо знать при расчетах газообмена помещения с внешней атмосферой, что будет показано в дальнейшем.

Степень нагретости газовой среды характеризуется в среднем отношением внутренней энергии этой среды к ее массе. Отношение этих физических величин можно представить с помощью формул в следующем виде:

.

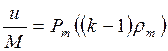Если правую и левую части равенства поделить на изохорную теплоемкость, то получится следующее выражение:

.

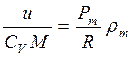Комплекс в левой части выражения имеет размерность «Кельвин». Этот комплекс представляет собой параметр состояния рассматриваемой термодинамической системы, который называется среднемассовой температурой газовой среды, т.е.

.

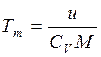С помощью выражения можно преобразовать формулу и в результате получить следующее уравнение:

.

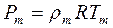Это уравнение связывает между собой три параметра состояния. По внешнему виду это уравнение такое же, как уравнение Клапейрона для локальных параметров состояния. В дальнейшем уравнение для краткости будем называть усредненным уравнением состояния газовой среды, заполняющей помещение.

Представляется интересным вопрос о том, как выражается средне-массовая температура, через локальные значения температур. Этот вопрос возникает при постановке натурных экспериментов. Ограничимся здесь анализом этого вопроса применительно к пожарам, протекающим без взрывов, сопровождающихся ударными волнами. Особенностью таких пожаров является то обстоятельство, что значения локальных абсолютных давлений во всех точках внутри помещения отличаются очень незначительно от среднеобъемного давления на всех этапах развития пожара. Другими словами, при таких пожарах отношение локального абсолютного давления в каждой точке внутри помещения к среднеобъемному давлению почти не отличается от единицы.

Чтобы получить формулу, с помощью которой можно вычислить среднемассовую температуру при известном распределении локальных температур по объему помещения, воспользуемся усредненным уравнением состояния, которое преобразуем с помощью уравнения Клапейрона

,

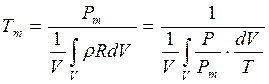T - локальная температура, К.

С учетом того, что преобразуется в следующее:

.

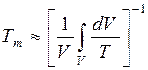Формула позволяет вычислить среднемассовую температуру, если известно распределение локальных температур по объему помещения (например, если в натурном эксперименте измерены локальные температуры в достаточно большом количестве точек внутри помещения).

С формальных позиций формулу можно рассматривать как один из методов осреднения всех значений локальных температур. Наряду с этим в практике экспериментальных исследований пожаров используется метод осреднения всех значений локальных температур с помощью следующей формулы:

,

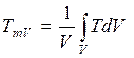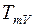- среднеобъемная температура среды, К.

Среднеобъемная температура и среднемассовая температура при однородном температурном поле равны друг другу. При неоднородном температурном поле эти температуры, вообще говоря, неодинаковы. Различие этих температур тем больше, чем больше неоднородность температурного поля.

Характер развития пожара в помещении зависит от размеров проемов и их расположения, вида и количества горючего материала, теплофизических свойств ограждающих конструкций и других факторов. Пожары в помещениях можно разделить с позиций термогазодинамического анализа на группы (классы). Пожары, входящие в одну группу, описываются одинаковыми по форме размерными уравнениями и условиями однозначности. В частности, пожары можно относить к одной группе лишь в том случае, если они протекают в геометрически подобных помещениях. Условия подобия можно установить при помощи хорошо разработанных в теплофизике методов. Одним из методов анализа подобия является метод приведения уравнений пожара к безразмерному виду.

Аналитическое решение системы дифференциальных уравнений, описывающих развитие пожара, может быть получено лишь для частных случаев. В общем случае система решается численными методами.

Перед тем как приступить к численному решению системы уравнений, описывающих пожар при указанных выше условиях, целесообразно привести уравнения пожара к безразмерному виду.

Дифференциальные уравнения пожара, входящие в интегральную модель, были сформулированы в 1976 году профессором Ю.А. Кошмаровым. Позднее, в 1987 году, уравнения Ю.А. Кошмарова были дополнены его учеником Ю.С. Зотовым уравнением, описывающим в общем виде изменение средней оптической концентрации дыма с течением времени.

Уравнения пожара вытекают, как и большинство уравнений математической физики, из фундаментальных законов природы - первого закона термодинамики для открытой термодинамической системы и закона сохранения массы.

Первое уравнение - уравнение материального баланса пожара в помещении - вытекает из закона сохранения массы. Применительно к газовой среде, заполняющей помещение, этот закон можно сформулировать так: изменение массы газовой среды в помещении за единицу времени равно алгебраической сумме потоков массы через границы рассматриваемой термодинамической системы. Внутренний объем пространства горящего помещения называется свободным объемом помещения и обозначается буквой V; G_в - расход поступающего воздуха из ограждающей атмосферы в помещение, который имеет место в рассматриваемый момент времени процесса развития пожара, кг/с; G_г - расход газов, покидающих помещения через проемы, в рассматриваемый момент времени, кг/с; y - скорость выгорания (скорость газификации) горючего материала в рассматриваемый момент времени, кг/с; r_mV - масса газовой среды, заполняющей помещение в рассматриваемый момент времени, кг.

За малый промежуток времени, равный dt, будет иметь место малое изменение массы газовой среды. В тоже время можно считать, что значения G_г, G_в и y в течении этого малого промежутка времени остаются практически неизменными. Тогда уравнение материального баланса для газовой среды в помещение записывается следующим образом

,

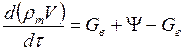где левая часть уравнения есть изменение массы газовой среды за единицу времени на интервале, равном, dt. Правая часть есть алгебраическая сумма потоков массы.

Аналогично можно получить дифференциальные уравнения баланса массы кислорода, баланса продуктов горения и баланса оптического количества дыма.

Уравнение баланса массы кислорода:

.

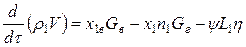Уравнение баланса токсичного продукта горения:

.

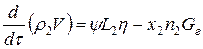Уравнение баланса оптического количества дыма:

.

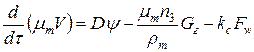где r ₁ - среднеобъемная парциальная плотность кислорода, кг×м^-3;

r ₂ - среднеобъемная парциальная плотность токсичного продукта горения, кг×м^-3;

m_m - среднеобъемная оптическая концентрация дыма, Нп×м^-1;

x _{1 в} - массовая доля кислорода в поступающем воздухе (x _{1 в} = 0,27);

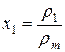- средняя массовая доля кислорода в помещении;

L ₁ - стехиометрический коэффициент для кислорода (количество кислорода, необходимое для сгорания единицы массы горючего материала), кг/кг;

h - коэффициент полноты сгорания;

n ₁ - коэффициент, учитывающий отличие концентрации кислорода в уходящих газах от среднеобъемной концентрации кислорода;

L ₂ - стехиометрический коэффициент для продукта горения (количество продукта горения, образующегося при сгорании единицы массы горючего материала), кг/кг;

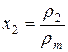- средняя массовая доля токсичного газа в помещении;

n ₂ - коэффициент, учитывающий отличие концентрации токсичного газа в уходящих газах от среднеобъемной концентрации этого газа;

n ₃ - коэффициент, учитывающий отличие оптической концентрации дыма в уходящих газах от среднеобъемного значения оптической концентрации дыма;

F_w - площадь поверхности ограждений (потолка, пола, стен), м²;

k_c - коэффициент седиментации частиц дыма на поверхностях ограждающих конструкции, Нп×с^-1. Коэффициент седиментации по физическому смыслу есть скорость осаждения частиц дыма.

На основе первого закона термодинамики можно вывести уравнение энергии пожара.

Рассматриваемая термодинамическая система, т.е. газовая среда внутри контрольной поверхности, характеризуется тем, что она не совершает работы расширения или другой механической работы. Кинетическая энергия видимого движения газовой среды в помещении пренебрежимо мала по сравнению с ее внутренней энергией. Потоки массы через некоторые участки контрольной поверхности (проемы) характеризуются тем, что в них удельная кинетическая энергия газа пренебрежимо мала по сравнению с удельной энтальпией.

Исходя из этого, получим уравнение энергии пожара

.

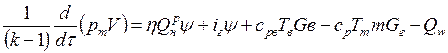Левая часть этого уравнения есть скорость изменения внутренней тепловой энергии газовой среды в помещении за единицу времени в рассматриваемый малый промежуток времени dt, т.е.

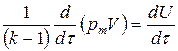, Вт.

Где i_г - есть энтальпия этих продуктов.

Представленные выше пять дифференциальных уравнений содержат шесть неизвестных функци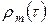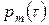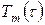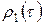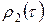й - , , , , и 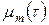. Эту систему уравнений дополняет алгебраическое уравнение - усредненное уравнение состояния.

Начальные значения для этих функций задаются условиями, которые имеют место в помещении перед началом пожара, т.е.

.

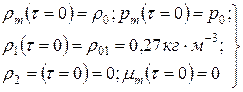Представленная здесь система уравнений описывает свободное развитие пожара.

Дата добавления: 2014-11-18