Проверка адекватности модели

Проверка значимости осуществляется на основе t – критерия Стьюдента, т.е. проверяется гипотеза о том, что параметр, измеряющий связь, равен нулю.

Средняя ошибка параметра равна:

, (76) а для параметра :

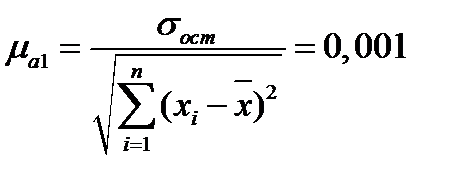. (77)

Расчетные значения t - критерия вычисляются по формуле:

(78) Параметр считается значимым, если 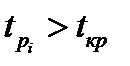. Значение определяется по формуле СТЬЮДЕНТ.ОБР(0,95;46) при числе степеней свободы 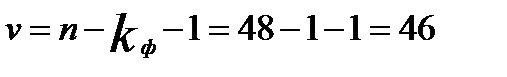и с вероятностью (Р=1- ) При и 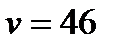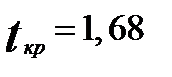. Следовательно, в рассматриваемом примере параметры 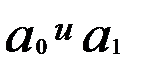являются значимыми.

Параметр 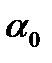лежит в пределах ; ,

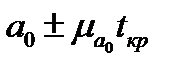а параметр - ; .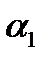

Значимость уравнения регрессии в целом определяется с помощью F – критерия Фишера:

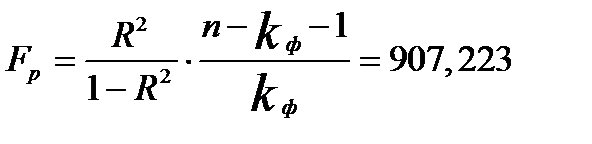(79)

Расчетное значение F сопоставляется с критическим для числа степеней свободы 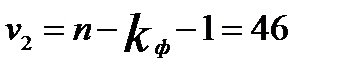при заданном уровне значимости 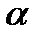(например, 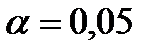), где , .

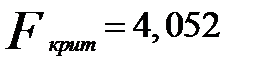Если , то уравнение считается значимым.

Другой подход к определению значений параметров уравнения парной регрессии и оценке значимости заключается в обращении к режиму “РЕГРЕССИЯ” EXCEL. Следует отметить, что результаты расчётов, приведенные в табл.7-9, получены с меньшими временными затратами и полностью совпадают с результатами “ручного” счёта.

Проверка наличия или отсутствия систематической ошибки

1. Проверка свойства нулевого среднего.

Рассчитывается среднее значение ряда остатков (табл. 10):

. (80)

Если оно близко к нулю, то считается, что модель не содержит систематической ошибки и адекватна по критерию нулевого среднего, иначе – модель неадекватна по данному критерию. Если средняя ошибка не точно равна нулю, то для определения степени ее близости к нулю используется t – критерий Стьюдента. Расчётное значение критерия вычисляется по формуле

(81)

и сравнивается с критическим .Если выполняется неравенство , то модель неадекватна по данному критерию.

2. Проверка случайности ряда остатков.

Осуществляется по методу серий. Серией называется последовательность расположенных подряд значений ряда остатков, для которых разность (графа 4 табл. 7.4) имеет один и тот же знак, где - медиана ряда остатков, значение которой рассчитано по данным графы 3 упомянутой таблицы.

Если модель хорошо отражает исследуемую зависимость, то она часто пересекает линию графика исходных данных и тогда серий много, а их длина невелика. Иначе – серий мало и некоторые из них включают большое число членов.

В качестве серий рассматриваются расположенные подряд ошибки с одинаковыми знаками. Далее подсчитывается число серий 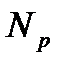и длина максимальной из них 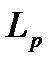. Полученные значения сравниваются с критическими

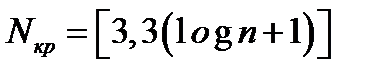(82) 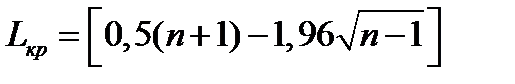(83) (квадратные скобки означают округление вниз до ближайшего целого).

Если выполняется система неравенств:

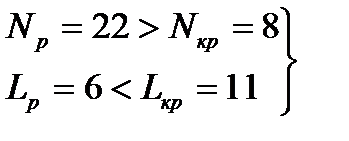, (84) то модель признается адекватной по критерию случайности, если хотя бы одно из неравенств нарушено, то модель признается неадекватной по данному критерию.

3. Проверка независимости последовательных остатков.

Является важнейшим критерием адекватности модели и осуществляется с помощью коэффициента Дарбина-Уотсона:

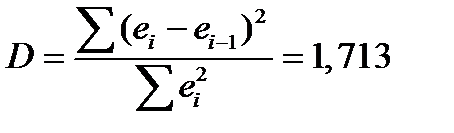. (85) Для рядов с тесной взаимосвязью между последовательными значениями остатков значение 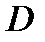близко к нулю, что свидетельствует о том, что закономерная составляющая не полностью отражена в модели и частично закономерность присуща ряду остатков, т.е. модель неадекватна исходному процессу.

Если последовательные остатки независимы, то 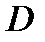близко к 2. Это свидетельствует о хорошем качестве модели и чистой фильтрации закономерной составляющей.

При отрицательной автокорреляции остатков (строго периодичном чередовании их знаков) 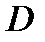близко к 4.

Для проверки существенности положительной автокорреляции остатков значение 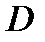сравнивается с 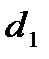и 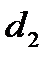из табл. 2 Приложения к лекции:

· если 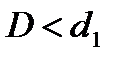, то гипотеза о независимости остатков отвергается и модель признается неадекватной по критерию независимости остатков;

· если 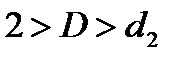, то гипотеза о независимости остатков принимается и модель признается адекватной по данному критерию (в рассматриваемом примере );

· если 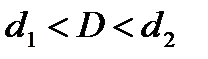, то значение критерия лежит в области неопределенности.

Если , то возникает предположение об отрицательной автокорреляции остатков, и тогда с критическими значениями сравниваются не 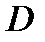, а 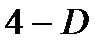и делаются аналогичные выводы.

4. Проверка постоянства дисперсии остатков.

Если на графике остатков они укладываются в симметричную относительно нулевой линии полосу шириной 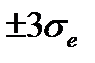(модуль стандартных остатков меньше 3) и не имеют как положительной так и отрицательной тенденций, то дисперсии ошибок наблюдений можно считать постоянными.

Значения стандартных остатков вычисляются по формуле

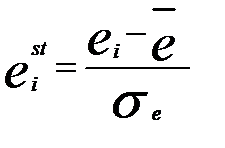, где 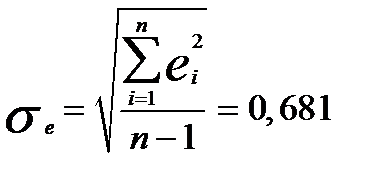и приведены в графе 5 табл.7.4.

Рис. 7.3 График стандартных остатков

Кроме визуальной оценки постоянства дисперсии существуют и более точные методы, например, тест Гольдфельда-Квандта. Суть теста заключается в следующем. Все n наблюдений упорядочиваются по возрастанию значений независимой переменной (x) и производится оценка параметров регрессий для первых и последних наблюдений с помощью метода наименьших квадратов. Для наибольшей мощности теста рекомендуется выбирать значение порядка n /3. Далее вычисляется расчётное значение статистики Фишера

, (86)

где - суммы квадратов остатков для первых и последних наблюдений соответственно. Далее задаётся уровень значимости 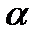и определяется с помощъю статистических таблиц. .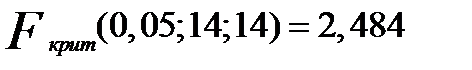

Если 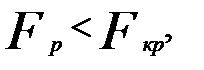то делается вывод о постоянстве дисперсии.

По совокупности четырех критериев делается вывод о принципиальной возможности использования модели: если модель адекватна по критериям постоянства дисперсий и нулевого среднего и хотя бы по одному из двух других критериев, то она может быть принята для использования, хотя и не признается полностью адекватной.

Дата добавления: 2014-11-18