Урок № 36. Контрольні запитання

Контрольні запитання

1. Чи правильні твердження:

· кожний тригонометричний ряд є функціональним рядом;

· кожний функціональний ряд є рядом тригонометричним;

· якщо тригонометричний ряд (1) є рівномірно збіжним до функції f на відрізку 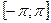, то (1) є рядом Фур’є функції f;

· якщо тригонометричний ряд (1) збігається до функції f на інтервалі(-∞; + ∞), то f є 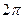– періодичною функцією;

· якщо функція f інтегрована на відрізку 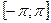і непарна, то її коефіцієнти Фур’є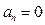 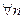, а .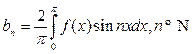

2. Розкласти в ряд за синусами функцію 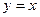на відрізку [0; 1].

Література: [1], §84, §85

Тема: Застосування рядів до наближених обчислень.

План:

1. Обчислення значень функцій.

2. Обчислення визначених інтегралів.

3. Розв’язування диференціальних рівнянь.

Елементарні функції можна розкласти в ряд:

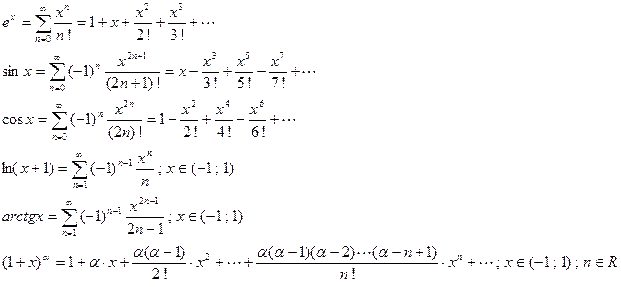
Користуючись розкладом у степеневі ряди, можна обчислювати наближені значення визначених інтегралів, границі та інше. У таких обчисленях зберігають п перших членів ряду, а останні відкидають. Для оцінки похибки знайденого наближеного значення потрібно оцінити суму відкинутих членів. На практиці оцінку проводять так: якщо ряд знакосталий, то його залишок порівнюють з геометричним рядом, члени якого утворюють спадну геометричну прогресію, а якщо ряд знакозмінний і його члени задовольняють умовам Лейбніца, то використовують оцінку 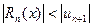, де 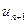- перший з відкинутих членів ряду.

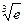Приклад. Використовуючи розклад функції в ряд обчислити значення виразу з точністю до 0,001:.

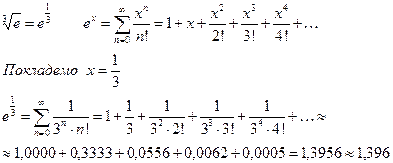
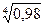Завдання. Використовуючи розклад функції в ряд обчислити значення виразу з точністю до 0,001:.

Дата добавления: 2014-11-18