Реализация пропускной способности систем и минимаксные свойства распределений

Рассмотрим важную задачу максимизации скорости передачи информации по каналам с переменными параметрами.

Скорость передачи информации в каналах с медленными общими замираниями можно рассматривать как медленно меняющуюся функцию времени вида [1]:

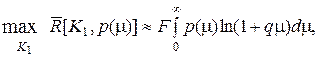(6.4)

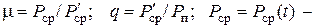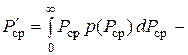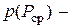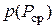где средняя мощность сигнала, медленно изменяющаяся во времени; математическое ожидание средней мощности; плотность вероятности ; плотность вероятности (передаточной функции канала по мощности); 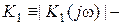модуль передаточной функции предыскажающего фильтра на входе канала, выполняющего роль статистического согласования источника сигнала с каналом связи; 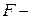эффективная полоса частот канала; средняя мощность аддитивной помехи в канале.

В условиях конфликтной ситуации между оператором системы передачи информации (СПИ) и системой радиопомех (СРП) или «природой» необходимо применять теоретико-игровой подход. Если аддитивную помеху считать белой, то под СРП подразумевается мультипликативная помеха (канал с медленными общими замираниями). Для игровой ситуации (см. [1]) справедливо неравенство

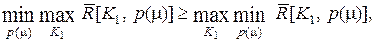(6.5)

где стратегиями СПИ и СРП соответственно являются выборы 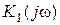и

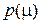
(6.6)

Поскольку функционал (6.4) с наложенной связью (6.6) линеен относительно 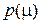, необходимо ввести другое дополнительное условие, например фиксацию энтропии распределения :

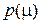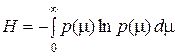. (6.7)

При этом экстремальное распределение находится решения вариационного уравнения Эйлера – Лагранжа

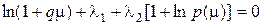, (6.8)

получаемого дифференцированием по 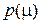подынтегральных выражений (6.4, 6.6, 6.7). Здесь 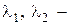множители Лагранжа, определяющиеся из дополнительных условий (6.6) и (6.7).

Решая вариационную задачу, находим

, (6.9)

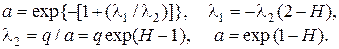
Подставляя значение 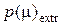из выражения (6.9) в равенство (6.4) и проводя интегрирование, находим

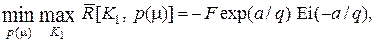(6.10)

где 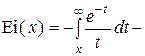интегральная показательная функция [22].

Если воспользоваться известным из теории игр [1, 23] равенством для цены игры

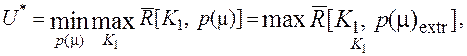(6.11)

то получаем

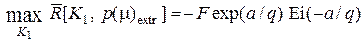. (6.12)

С учетом равенств (6.10) и (6.12) доказано, что неравенство (6.5) превращается в равенство, т. е. существует цена игры (минимаксное значение скорости передачи информации):

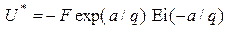. (6.13)

Оптимальными (минимаксными) стратегиями СПИ и СРП соответственно являются обеспечение равномерного спектра сигнала на выходе оптимального предыскажающего фильтра (при аддитивном белом шуме, действующем в канале связи) и экспоненциальность распределения 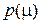(выражение (6.9)). Таким образом, доказана минимаксность экспоненциального распределения в каналах с медленными общими замираниями.

При , т. е. 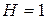, из равенства (6.13) получаем известную формулу Сифорова для пропускной способности С каналов с медленными общими замираниями:

. (6.14)

Следовательно, в каналах с медленными общими замираниями можно передавать информацию со скоростью, равной пропускной способности канала с экспоненциальным или рэлеевским распределением, поскольку выражение (6.14) справедливо для рэлеевского распределения вероятностей.

Условная величина пропускной способности для каналов с медленными общими замираниями может быть определена по формуле [1]

, (6.15)

где 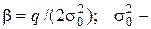средняя мощность рассеянной составляющей флуктуирующего сигнала.

Дата добавления: 2014-11-18