Приклад 7.3

Погрешности в радиотехнических измерениях.

7.2.1. Абсолютная и относительная погрешности, точность измерений.

Абсолютной погрешностью измерения называется алгебраическая разность между измеренным 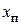и истинным 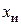значениями измеряемой величины:

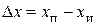. (7.1)

Абсолютная погрешность 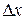может быть положительной и отрицательной; в тех случаях, когда знак погрешности неизвестен, перед 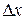ставят знак ±.

Отношение абсолютной погрешности к истинному значению измеряемой величины называют относительной погрешностью, которая выражается в долях измеряемой величины либо в процентах:

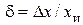або 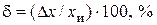. (7.2)

Относительная погрешность обычно играет более существенную роль в метрологии, чем абсолютная, так как первая связана с характеристикой точности измерений.

Точностью измерений характеризуется близость результатов измерений к истинному значению измеряемой величины. Количественно точность измерений определяется величиной, обратной относительной погрешности 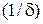. Так, если относительная погрешность 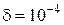, то точность измерений составляет .

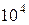7.2.2. Систематические погрешности.

Как уже отмечалось, в метрологии разделяют погрешности измерения на:

1) систематические;

2) случайные;

3) грубые (промахи).

К систематическим погрешностям измерения относятся составляющие погрешности, которые входят с постоянной величиной и знаком в данную серию измерений (опытов) или закономерно изменяются при повторных измерениях одной и той же величины.

Систематическую погрешность, например, вносит смещение нулевой точки шкалы миллиамперметра: если стрелка шкалы при отсутствии тока стоит на делении 1.2 мА, то во все измерения на этом приборе входит систематическая погрешность 1.2 мА.

Согласно источнику происхождения, можно разделить систематические погрешности на следующие разновидности.

Ø Инструментальные погрешности обусловливаются средствами измерения (приборами). Эти погрешности возникают вследствие свойств измерительной аппаратуры (недостатки конструкции, технологии, неточности градуировки шкал приборов и пр.).

Ø Установочные погрешности обусловливаются специфическим расположением средств измерения (отклонение гальванометров от вертикального направления, влияние ориентации магниточувствительных приборов относительно магнитного поля Земли и др.).

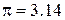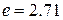Ø Методические погрешности возникают в результате упрощения расчетной формулы для измеряемой величины, а также вследствие ограниченной точности физических констант, входящих в расчеты. Так, например, при использовании известных постоянных и , которые являются округленными значениями дуговой меры и основания натуральных логарифмов. Более точные значения этих констант соответственно равны 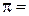3.141593; 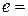2,718282.

Ø Погрешности вычислений обусловлены приближенными вычислениями: округлением результатов вычислений; применением линеаризации, аппроксимации, интерполяции.

Ø Внешние погрешности возникают в результате влияния на результат измерений свойств внешней среды и внешних условий: вибрации, тряски, электромагнитных помех, влажности и давления воздуха, температуры окружающей среды и др.

Ø Личные, или субъективные, погрешности вносятся в процесс измерений человеком-оператором (наблюдателем) и обусловлены особенностями психофизиологического восприятия сигнала-раздражителя (чувствительность органов слуха и зрения, степень утомляемости, быстрота реакции и пр.).

По характеру изменения систематические погрешности делятся на постоянные и прогрессивные. Постоянную систематическую погрешность невозможно обнаружить по результатам идентичных измерении. Полученные, например, результаты измерения частоты: 15.3; 15.6; 15.4 МГц не позволяют выявить систематическую погрешность. Для ее обнаружения необходимо провести специальные контрольные измерения этих частот с использованием, например, первичного эталона частоты. При этом сравнительный анализ результатов обнаружит наличие систематической погрешности у неэталонного частотометра. Прогрессивные погрешности в данной серии измерений (опытов, экспериментов) непрерывно возрастают или убывают, как, например, погрешность, обусловленная постепенным уменьшением напряжения источника питания в измерительной цепи.

Для уменьшения систематических погрешностей применяют следующие способы:

Ø тщательную регулировку и юстировку средств измерений, устранение внешних влияний путем экранирования, термостатирования и т. д.;

Ø расчет систематической погрешности и введение поправки, которую алгебраически добавляют к неверному значению измеряемой величины;

Ø организацию процесса измерений таким образом, чтобы в среднем результате происходила компенсация различных систематических погрешностей измерения (применение экспертных оценок, рандомизация последовательности опытов и пр.).

7.2.3. Случайные погрешности. Статистические характеристики результатов измерения.

Кроме постоянно действующих причин, обусловливающих появление систематических погрешностей, на результат измерения влияют разнообразные случайные факторы, которые меняются от измерения к измерению: колебания климатических условий (давления, влажности, температуры), случайное положение глаза человека-оператора при отсчете результата измерения по шкале (ошибки на параллакс) и др. В результате влияния случайных факторов вносится случайная погрешность. Случайной погрешностью называется составляющая погрешности измерения, значение которой меняется случайным образом при повторных измерениях одной и той же величины.

Случайные погрешности в радиотехнике, вызванные различного рода шумами самих элементов радиоприемного устройства, атмосферными, ионосферными, галактическими и т. д., помехами естественного и искусственного происхождения, также требуют оценки и учета при проектировании и эксплуатации различного назначения радиотехнических систем.

Случайная погрешность обнаруживается в процессе измерений лишь тогда, когда измерительный прибор обладает достаточно высокой чувствительностью для выявления влияния случайных факторов. Предположим, например, что при измерении чувствительности радиоприемного устройства результаты трех измерений оказались равными соответственно 1.30; 1.25; 1.35 мкВ. Случайными факторами, приведшими к рассеянию результатов, могли оказаться: нестабильность частоты генератора стандартных сигналов; неточность установки лимбов «напряжение» и «частота» вследствие оптического параллакса; воздействие внешних помех в результате плохой экранировки эквивалента антенны радиоприемника; флуктуации источников питания экспериментальной установки. Изучение случайных погрешностей основано на применении теории вероятностей и математической статистики.

Математические законы теории вероятностей не являются беспредметными абстракциями, лишенными физического содержания; они представляют собой математическое выражение реальных закономерностей, фактически существующих в массовых случайных явлениях природы. Каждое исследование случайных явлений, выполняемое методами теории вероятностей, прямо или косвенно опирается на экспериментальные данные. Оперируя такими понятиями, как события и их вероятности, случайные величины, их законы распределения и числовые характеристики, теория вероятностей дает возможность теоретическим путем определять вероятности одних событий через вероятности других, законы распределения и числовые характеристики одних случайных величин через законы распределения и числовые характеристики других. Такие косвенные методы позволяют значительно экономить время и средства, затрачиваемые на эксперимент, но отнюдь не исключают самого эксперимента. Каждое исследование в области случайных явлений, как бы отвлеченно оно ни было, корнями своими всегда уходит в эксперимент, в опытные данные, в систему наблюдений.

Разработка методов регистрации, описания и анализа статистических экспериментальных данных, получаемых в результате наблюдения массовых случайных явлений, составляет предмет специальной науки – математической статистики.

Все задачи математической статистики касаются вопросов обработки наблюдений над массовыми случайными явлениями, но в зависимости от характера решаемого практического вопроса и от объема имеющегося экспериментального материала эти задачи могут принимать ту или иную форму.

Охарактеризуем вкратце некоторые типичные задачи математической статистики, часто встречаемые на практике.

Œ. Задача определения закона распределения случайной величины по статистическим данным

Закономерности, наблюдаемые в массовых случайных явлениях, проявляются тем точнее и отчетливее, чем больше объем статистического материала. При обработке обширных по своему объему статистических данных часто возникает вопрос об определении законов распределения тех или иных случайных величин. Теоретически при достаточном количестве опытов свойственные этим случайным величинам закономерности будут осуществляться сколь угодно точно. На практике нам всегда приходится иметь дело с ограниченным количеством экспериментальных данных; в связи с этим результаты наблюдений и их обработки всегда содержат больший или меньший элемент случайности. Возникает вопрос о том, какие черты наблюдаемого явления относятся к постоянным, устойчивым и действительно присущи ему, а какие являются случайными и проявляются в данной серии наблюдений только за счет ограниченного объема экспериментальных данных. Естественно, к методике обработки экспериментальных данных следует предъявить такие требования, чтобы она, по возможности, сохраняла типичные, характерные черты наблюдаемого явления и отбрасывала все несущественное, второстепенное, связанное с недостаточным объемом опытного материала. В связи с этим возникает характерная для математической статистики задача сглаживания или выравнивания статистических данных, представления их в наиболее компактном виде с помощью простых аналитических зависимостей.

. Задача проверки правдоподобия гипотез

Эта задача тесно связана с предыдущей. При решении такого рода задач мы обычно не располагаем настолько обширным статистическим материалом, чтобы выявляющиеся в нем статистические закономерности были в достаточной мере свободны от элементов случайности. Статистический материал может с большим или меньшим правдоподобием подтверждать или не подтверждать справедливость той или иной гипотезы. Например, может возникнуть такой вопрос: согласуются ли результаты эксперимента с гипотезой о том, что данная случайная величина подчинена закону распределения 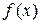?Другой подобный вопрос: указывает ли наблюденная в опыте тенденция к зависимости между двумя случайными величинами на наличие действительной объективной зависимости между ними или же она объясняется случайными причинами, связанными с недостаточным объемом наблюдений? Для решения подобных задач математи­ческая статистика выработала ряд специальных приемов.

Ž Задача нахождения неизвестных параметров распределения

Часто при обработке статистического материала не возникает вопрос об определении законов распределения исследуемых случайных величин. Обычно это бывает связано с недостаточным объемом экспериментального материала. Иногда же характер закона распределения качественно известен до опыта, из теоретических соображений; например, часто можно утверждать заранее, что случайная величина подчинена нормальному закону. Тогда возникает более узкая задача обработки наблюдений – определить только некоторые параметры (числовые характеристики) случайной величины. При небольшом числе опытов задача более или менее точного определения этих параметров не может быть решена; в этих случаях экспериментальный материал содержит в себе неизбежно значительный элемент случайности; поэтому случайными оказываются и все параметры, вычисленные на основе этих данных. В таких условиях может быть поставлена только задача об определении так называемых оценок для искомых параметров, т. е. таких приближенных значений, которые при массовом применении приводили бы в среднем к меньшим ошибкам, чем всякие другие. С задачей отыскания оценок числовых характеристик тесно связана задача оценки их точности и надежности.

Таков далеко не полный перечень основных задач математической статистики. Мы перечислили только те из них, которые наиболее важны для нас по своим практическим применениям. В настоящем разделе и в разделе 8 мы вкратце познакомимся с некоторыми, простыми, элементарными задачами математической статистики и с методами их решения.

Оценка измеряемого параметра. Если предположить, что при прямом измерении искомого параметра 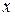случайная погрешность намного больше систематической погрешности средств измерения, исходя из постулата о среднем арифметическом, согласно которому наивероятнейшим значением 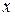из ряда независимых наблюдений при нормально распределенных ошибках будет их среднее арифметическое :

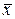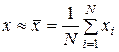, (7.3)

где 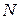– общее число наблюдений (объем выборки).

Из теории вероятностей известно, что среднее арифметическое ряда наблюдений нормально распределенной величины X есть также нормальная величина с тем же математическим ожиданием 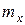и со среднеквадратическим отклонением (СКО) 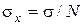, где 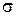– СКО отдельного наблюдения (опыта). Последнее означает, что область рассеивания среднего арифметического в разных рядах наблюдений по 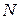наблюдений в каждом будет в 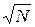раз меньше области рассеивания результатов отдельного наблюдения. Зона рассеивания случайной величины характеризуется дисперсией 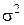и СКО .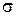

Среднее арифметическое (7.3) обеспечивает наилучшую оценку среднего значения только при нормальном распределении, наиболее распространенном среди случайных процессов, особенно при достаточно большом числе независимых случайных величин с одинаковым распределением вероятностей (закон больших чисел). Для других распределений ошибок среднее арифметическое не дает наилучшую, оценку. Так, например, при равномерном распределении наилучшей оценкой среднего значения 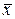является полусумма крайних членов:

.

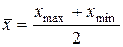Оценка СКО группы наблюдений.

Оценка среднеквадратического отклонения группы отдельных наблюдений находится по формуле

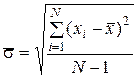. (7.4)

Оценка СКО среднего арифметического результата измерения.

Если 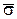определяет СКО отдельных наблюдений, то 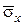– рассеивание результатов измерений, т. е. выборочное среднее арифметическое, получаем как

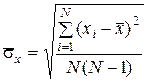. (7.5)

В случае большого числа наблюдений 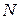эмпирические оценки по формулам (7.4), (7.5) близки к истинным.

В тех случаях, когда погрешность средств измерения намного превосходит случайную погрешность, за предельную погрешность однократного или совпадающих многократных прямых наблюдений, а также за погрешность измерений, в которых случайная составляющая намного меньше систематической, следует принять предел систематической погрешности средства измерения.

Если систематическая и случайная погрешности измерения соизмеримы, то предел суммарной погрешности результата измерений можно определить как

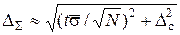, (7.6)

где 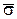– оценка СКО результатов наблюдений по формуле (7.4); 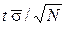случайная составляющая погрешности измерения; 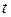– параметр Стьюдента, равный 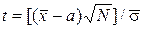при доверительной вероятности 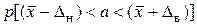, характеризующей точность измерений (В табл. Б2 додатку Б приведены квантили распределения Стьюдента); 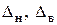– соответственно нижняя и верхняя границы интервала; 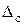– предельное значение систематической погрешности.

7.2.4. Статистические характеристики результатов косвенных измерений.

В радиотехнике во многих случаях используются косвенные измерениияя. Например, чтобы найти сопротивление некоторого резистора 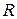, к нему прикладывают напряжение 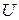, измеряют ток 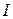, протекающий через резистор и определяют сопротивление 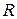как . Это самый простой пример косвенных измерений.

Вправа 7. 2

Наведіть 2 –3 приклади непрямих вимірів у радіотехніці і телекомунікації.

В связи с этим часто важно при выполнении НДР проводить анализ статистических характеристик оценок погрешностей косвенных измерений. При косвенных измерениях искомая величина 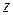не измеряется непосредственно, а рассчитывается по формуле 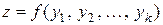, которая связывает ее с величинами 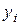, оценки которых можно получить прямыми измерениями. В тех случаях, когда результаты прямых измерений содержат случайную погрешность, функция 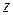является также случайной. Ниже приводятся расчетные формулы для оценки числовых характеристик при косвенных измерениях.

Оценка среднего значения функции.

,

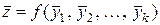где 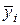– среднее арифметическое аргумента .

Оценка СКО случайной составляющей погрешности.

Если 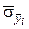– оценка СКО среднего арифметического , определяемая по формуле (7.5), то СКО случайной составляющей погрешности будет

,

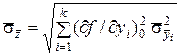где 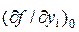– частная производная функции по аргументу ,в выражение которой подставлены значения средних арифметических .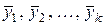

В последующих главах данного раздела приведены основы теории планирования экспериментов, где могут быть использованы рассмотренные методы оценки погрешностей измерения. Прежде, чем рассмотреть основы теории планирования экспериментов, необходимо хотя бы кратко ознакомиться с некоторыми правилами отбора и простыми (традиционными) алгоритмами планирования экспериментов, базирующихся на методах математической статистики.

7.3. Простые правила и алгоритмы планирования экспериментов [19, 20]

7.3.1. Способы отбора.

Применение методов математической статистики к обработке наблюдений основано на глубокой аналогии между производством наблюдений и отбором из некоторой генеральной совокупности. При этом в качестве генеральной совокупности рассматривается чисто гипотетическая совокупность всех возможных результатов наблюдений при данном комплексе условий испытания. Отбор данных из этой совокупности производится в процессе наблюдений независимо от нашей воли. Из-за этого основным фактором отбора наблюдений всегда является случайность, что и позволяет применять для обработки наблюдений основные положения теории вероятностей.

Отбор данных, происходящий помимо нашей воли, можно назвать естественным отбором;именно таким является отбор данных при наблюдениях. Однако при производстве наблюдений и при дальнейшей их обработке часто возникает необходимость и в других, искусственных способах отбора. Например, при анализе вещества приходится делать пробы из разных участков, чтобы нейтрализовать возможную неоднородность материала; отбор проб при этом находится целиком в нашем распоряжении. При контроле за производством приходится выбирать образцы из общей продукции. При различных экономических и демографических исследованиях также нужен предварительный отбор объектов для изучения. Примеры таких случаев, когда исследователь вынужден делать сознательный выбор, можно еще долго продолжать; отметим лишь в заключение, что даже заготовленный уже цифровой материал может нуждаться в дополнительном отборе в целях сокращения объема, в целях удаления неподходящих данных и в целях проверки правильности и добросовестности полученных данных и подготовительных расчетов – подобный отбор также производится исследователем целиком по его воле.

Существует много способов искусственного отбора. Выбор того или иного способа зависит от цели отбора, от поставленной задачи. В самом общем плане способы отбора делятся на две группы: пристрастные и репрезентативные.

Пристрастными называются такие способы отбора, при которых отбираются элементы по какому-либо заранее намеченному признаку; при этом проверке подлежат все элементы совокупности, из которой делается отбор. Например, из совокупности чисел отбираются самых больших или отбираются все числа, не достигающие нужной величины. Пристрастный отбор применяют и для того, чтобы изъять все наблюдения, например, с нарушенными условиями испытания и является важной стадией эксперимента; его задача при этом состоит обычно в том, чтобы устранить все заметные нарушения условий испытания. С помощью пристрастного отбора нередко удается ликвидировать те или иные доминирующие (несимметричные) факторы, нарушающие нормальность распределения.

Пристрастный отбор всегда является сознательным с ясной характеристикой данных, подлежащих отбору, поэтому он редко вызывает затруднения. Сложнее обстоит дело со второй группой способов отбора.

Способы отбора называются репрезентативными, если отобранная группа элементов достаточно полно характе­ризует всю совокупность, из которой был сделан отбор. Разумеется, как бы ни был удачен отбор, в суждениях о всей совокупности будет элемент случайности. Более того, некоторые особенности всей совокупности вообще не отразятся на отобранной группе элементов, поэтому «репрезентативность» отбора, вообще говоря, является относительной и связана с конкретной числовой характеристикой совокупности, которая изучается с помощью отобранных элементов,

Фактически репрезентативный отбор применяется тогда, когда судить о характеристиках совокупности, используя все ее элементы, невозможно (либо слишком трудно или дорого) из-за того, что эта совокупность чересчур велика, а возможно, и не вся доступна анализу. Если объем 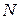этой совокупности очень велик, то его практически можно считать бесконечным. В этом случае заданную совокупность можно рассматривать как генеральную, а отобранные элементы как выборку, применяя в дальнейшем все достижения общего выборочного метода. Если же 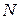не очень велико по сравнению с количеством отобранных элементов (скажем, 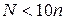), то с числом 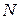нужно считаться при интерпретации результатов отбора.

Количество отбираемых элементов можно определить, если известна дисперсия 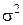изучаемой характеристики (по каким-либо предыдущим данным). Это количество будет зависеть от той точности, с которой мы хотим получить значение характеристики. Если эта точность задана допустимой дисперсией 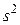, то определяется из формулы

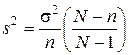, (7.7)

которая при очень больших 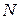принимает вид

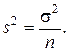(7.8)

Эту формулу легко объяснить: 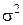есть как бы генеральная дисперсия, а 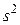есть дисперсия среднего выборки из элементов, которая всегда в раз меньше «одиночной» дисперсии.

Рассмотрим пример.

Пусть из предыдущих анализов известна дисперсия, связанная с неоднородностью некоторого вещества и равная 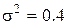. Допустим, что нам нужно знать содержание вещества с дисперсией 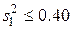причем на методику анализа приходится дисперсия 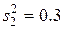(ошибка воспроизводимости). Это значит, что на долю неоднородности допускается оставить дисперсию .

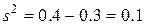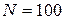
Розв‘язання.

Если в нашем распоряжении 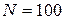измерений, то искомое число проб определится из равенства

,

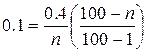т. е. равно четырем.

É

Выбор того или иного способа репрезентативного отбора зависит от степени знаний о всей совокупности. Если, например, известно, что элементы в совокупности расположены случайным образом, то можно применять механический отбор – отбирать каждый пятый или каждый десятый и т. п. элемент. Если же в последовательности элементов имеется некоторая ритмичность, то нужно применять аритмичный отбору например, в первой десятке брать первый элемент, во второй десятке – второй и т. д. Скажем, анализируя раз в день качество работы оборудования, мы не должны брать пробы в одно и то же время дня. Иногда вся совокупность заведомо разбивается на отдельные части, которые желательно равномерно учесть. В этом случае применяют типический отбор, т. е. отдельно отбирают элементы из каждой части и только сводят их в общую группу.

В тех случаях, когда о всей совокупности ничего не известно, единственной гарантией репрезентативности может служить случайный отбор. Для того чтобы отбор был случайным, нужно все элементы совокупности пронумеровать; номера отобранных элементов должны образовывать случайную последовательность чисел. В данном случае речь идет о том, чтобы создать случайную последовательность, собственной волей имитировать случай.

Имитация случая является весьма трудной задачей. Как бы вы ни старались, выписывая числа, делать их случайными, в них обязательно проявится (особенно при больших объемах) какой-то бессознательно выбранный вами план. На помощь приходит ЭВМ. При выполнении лабораторной работы №4 вы познакомитесь с тем, как можно генерировать псевдослучайные числа с заданным законом распределения.

7.3.2. Выбор числа наблюдений.

Увеличение числа параллельных наблюдений является основным способом повышения точности статистического анализа. Действительно, среднее выборки объема имеет дисперсию в раз меньше, чем одиночные наблюдения. Поэтому для определения необходимого числа наблюдений достаточно знать генеральную дисперсию наблюдений 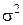и допустимую дисперсию результата 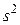; при этом .

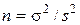Увеличивая , можно неограниченно повышать точность найденного результата, лишь бы только в процессе наблюдений не менялись условия испытания. Именно этим приемом пользуются, чтобы уменьшить доверительный интервал при неизменной доверительной вероятности.

Сложнее обстоит дело с выбором числа наблюдений при проверке гипотез. Это число должно одновременно служить двум целям: уменьшать вероятность 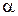ошибки первого рода (отклонение правильной гипотезы) и вероятность 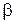ошибки второго рода (принятие неверной гипотезы). Первая вероятность совпадает с принятым уровнем значимости 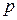. Вторая вероятность зависит от многих факторов и в первую очередь от того, насколько неверна принимаемая гипотеза. Поэтому под 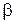понимают обычно наибольшую возможную вероятность ошибки второго рода при любых отклонениях от правильной гипотезы. Контроль за ошибками второго рода является трудной задачей, требуя специальных методов проверки гипотезы. Общий принцип такого контроля поясним на примере конкретной гипотезы. Але спочатку визначимо одну важливу для подальшого величину: квантіль.

Квантіль – у розподілі частот це точка, що поділяє дані у заданому співвідношенні, тобто квантілем 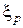розподілу випадкової величини 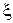з функцією розподілу 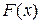звуть розв‘язання рівняння 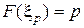. Іншими словами, квантіль 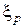є таким значенням випадковою величини 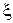, що 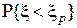. Квантілі стандартного нормального розподілу (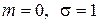) позначають 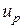. Їх лего знайти за таблицею Б1 додатку Б. Квантіль 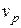загального нормального розподілу з параметрами 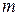і 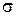визначається допомогою квантілів :

.

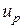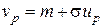Поняття квантіль використовують не тільки для нормального розподілу, але й для розподілів інших типів.

Рассмотрим пример.

Дата добавления: 2014-11-18