Приклад 7.8

В результате исследования влияния на процесс некоторого параметра 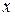получены данные 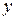, приведенные в таблице 7.1. Требуется описать эти данные линейным уравнением .

На рис. 7.4 приведены крестиками значения параметра 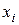в 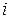-том эксперименте и соответствующее ему значение отклика .

Розв‘язання.

Для нахождения двух неизвестных коэффициентов можно ограничиться результатами двух опытов.

Рассчитаем 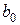и по результатам первых двух опытов. Запишем систему двух уравнений и найдем ее решение.

Таким образом, если учесть только два измерения (два первых крестика на графике рис. 7.4), получим – прямая 1 на рисунке.

Очевидно, если, например, взять результаты второго и третьего измерений (опытов), получим другое уравнение и, следовательно другую прямую на графике.

Вправа 7. 11

На рис. 7.4 наведено пряму, яка проходить через дві крайні (першу і одинадцяту) – пряма 2. Знайдіть рівняння цієї прямої.

É

Рассмотренный пример показал, что вычислительная процедура должна основываться на использовании всех экспериментальных данных. Алгоритм нахождения неизвестных коэффициентов уравнения в такой «переопределенной» задаче можно построить, если базироваться на признании вероятностной природы экспериментальных данных.

Ошибка в предсказании по найденному уравнению результата 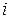-гоопыта характеризуется величиной невязки

,

где – предсказанное значение выхода процесса; – полученное в 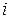-томопыте значение выхода процесса.

Примем, что невязка подчиняется нормальному закону распределения, то есть плотность вероятности появления любой 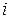-тойневязки имеет вид

.

Произведение плотностей вероятности появления невязок, вычисленных для каждого из N опытов эксперимента, называется функцией правдоподобия

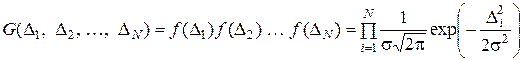
Чем больше величина функции правдоподобия, тем более точно уравнение описывает экспериментальные данные.

Совокупность коэффициентов уравнения, которая максимизирует функцию правдоподобия, наилучшей из всех других совокупностей при заданной структуре уравнения.

Функция правдоподобия достигнет максимума при минимизации суммы квадратов невязок. Следовательно, минимизация суммы квадратов невязок и будет условием получения максимально правдоподобных оценок коэффициентов аппроксимирующего уравнения при нормальном законе распределения вероятности результата измерений. Реализация этого условия при получении оценок коэффициентов уравнения названа методом наименьших квадратов (МНК).

МНК дает оценки коэффициентов аппроксимирующей зависимости, обладающие рядом оптимальных свойств независимо от закона распределения случайной величины. Иными словами, МНК может применяться и в тех случаях, когда экспериментатор не может на данном этапе исследования доказать нормальность закона распределения.

МНК позволяет сгладить влияние случайных причин на экспериментальные данные и получить математическую модель процесса в виде полинома той или иной степени.

Предположим, что исследуемый процесс будет описываться линейным уравнением

.

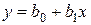Минимизируемая функция

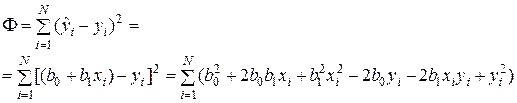
Чтобы найти экстремум этой функции, продифференцируем ее 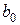по и по и приравняем две эти производные нулю.

Решив систему двух уравнений с двумя неизвестными (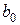 и ), найдем те значения, которые обеспечивают минимум суммы квадратов невязок.

Вправа 7.12

Доведіть, що знайдені коефіцієнти забезпечать саме мінімум функції .

Систему так называемых нормальных уравнений можно записать следующим образом:

В этом простейшем случае решение системы не вызывает больших трудностей

(7.21)

Вправа 7.13

Виведіть формули (7.21).

Дата добавления: 2014-11-18