Глобальні методи інтерполяції

Детерміновані методи просторової інформації

Глобальні методи інтерполяції одночасно використовують всі наявні дані для виконання прогнозу для всієї даної території, тоді як локальні методи оперують в межах невеликих зон навкруги належних інтерполяції вузлів для того, щоб забезпечити виконання оцінки тільки за даними, розміщеними у безпосередній близькості від точок прогнозу або оцінювання.

Глобальні інтерполяції зазвичай використовуються не для безпосередньої інтерполяції, а для дослідження і можливого видалення ефекту глобальних варіацій (тренда), обумовлених зовнішніми чинниками. Після того як глобальні ефекти будуть видалені, відхилення від глобальних варіацій можуть інтерполюватися з використанням локальних методів.

Глобальні методи зазвичай прості для обчислення і часто базуються на стандартних статистичних ідеях варіаційного аналізу і регресії. До них відносять (Burrough., McDonnel, 1998):

· класифікації з використанням зовнішньої інформації;

· поліноміальну регресію з геометричними координатами;

· регресійні моделі.

Класифікаційні методи використовують досяжну інформацію (таку, як ґрунтові типи або адміністративні території) для того, щоб розділити досліджувану територію на регіони, які можуть бути охарактеризовані статистичними моментами (середньою, дисперсією) атрибутів, виміряних у точках, розміщених у межах цих регіонів.

Методи поліноміальної регресії з геометричними координатами х, у використовують поліноми різних ступенів вигляду

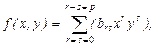(8.1)

де b_rs – коефіцієнти полінома; р – порядок полінома.

Перші чотири рівняння (8.1), тобто поліноми нульового, першого, другого і третього ступеня, є:

b00	горизонтальна площина
b00 + b10x + b01 y	похила площина
b00 + b10x + b01 y + b20 x^2+ b11 xy + b02 y^2	квадратична поверхня
b00 + b10x + b01 y + b20 x^2+ b11 xy + b02 y^2+ + b30 x^3+ b21 x^2y + b12 xy^2+ b03 y^3	кубічна поверхня

Поліном (8.1) представляє, по суті, рівняння трендової поверхні для заданого набору точкових значень. Ціле р є порядком трендової поверхні, для якої існує (p + 1)(p + 2) / 2 коефіцієнтів b_rs, які потрібно підібрати для того, щоб мінімізувати функціонал:

(8.2)

Таким чином, горизонтальна поверхня має порядок нуль, похила плоска поверхня – перший порядок, квадратична поверхня – другий порядок, кубічна поверхня з десятьма коефіцієнтами має третій порядок. Знаходження коефіцієнтів b_rs є стандартною процедурою в задачах на множинну регресію, тому обчислення легко виконуються за допомогою стандартних статистичних пакетів.

Після знаходження коефіцієнтів b_rs трендова поверхня може бути відображена оцінкою значень z(x, у) у всіх точках регулярної мережі.

Порядок трендової поверхні р з формальної точки зоруможе бути скільки завгодно великим. Збільшення порядку полінома, як правило, веде до збільшення ступеня його відповідності реальній поверхні. Проте при цьому, з одного боку, втрачається фізичне значення побудови, з іншого – різко збільшуються вимоги до обсягу даних, необхідних для знаходження коефіцієнтів b_rs.

Регресійні методи ґрунтуються на використовуванні можливого функціонального зв’язку між атрибутами, які легко вимірюються. Наприклад, концентрації забруднювача в ґрунті – від відстані до джерела забруднення, швидкості вітру – від шорсткості поверхні і т.п. Емпіричну регресійну модель часто називають трансформаційною функцією. Вона має вигляд

(8.3)

де b₀, b₁.,..., b_n – коефіцієнти регресії; A₁, A₂,..., A_n – незалежні характеристики (атрибути).

Дата добавления: 2014-11-18