Додаток №4

Додаток №3

Схема обчислення похибок для непрямих вимірювань

1. Для кожної серії вимірювань проводитися обробка, за схемою, описаною у додатку №2. При цьому для всіх вимірюваних величин задають одне і те ж значення надійності.

2. Обчислюється середнє значення шуканої величини: .

3. Обчилюються часткові похідні:

, , .

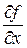4.Обчислюється похибка непрямих вимірювань:

.

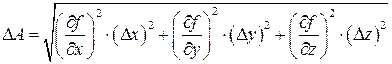5.Остаточний результат записується у вигляді:

,%

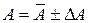
де – відносна похибка непрямих вимірювань.

Закони розподілу дискретних та неперервних величин

Закони розподілу дискретних величин

Біноміальний розподіл (розподіл Бернулі)

Цей розподіл справедливий тільки для дискретної випадкової величини Х, яка може приймати тільки цілі невід'ємні значення з ймовірностями , де - ймовірність появи події в кожному спостереженні, m - кількість сприятливих подій, n - загальна кількість випробувань, 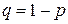. називається розподіленою за біноміальним законом з математичним сподіванням 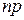, та дисперсією .

Закон Бернулі використовується тоді, коли необхідно знайти ймовірність появи випадкової події, яка реалізується 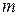раз у серії з 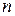випробувань.

Біноміальному закону розподілу підпорядковуються такі випадкові події, як число викликів швидкої допомоги за певний проміжок часу, черги до лікаря в поліклініці, епідемії тощо.

Розподіл Пуасона.

Дискретна випадкова величина X, яка може приймати тільки цілі невід'ємні значення з ймовірностями називається розподіленою за законом Пуассона з математичним сподіванням і дисперсією , де . Розглядаються малоймовірні події, які відбуваються у серії незалежних випробувань декілька разів. Розподіл Пуасона, як граничний біноміальний проявляється при розгляді випадкових процесів дискретної випадкової величини Х, яка неперервно залежить від часу. В медицині використовується при вирішенні задач надійності медичного обладнання та апаратури, розповсюдження епідемії, викликів до хворого дільничних лікарів та в інших задачах масового обслуговування.

Дата добавления: 2014-11-18