Способи завдання та дослідження функцій

Функцію можна задати різними способами. Найбільш поширені і важливі серед них – завдання функції формулою (аналітичний), табличний та графічний. При використанні ПК використовується також алгоритмічний спосіб.

Побудова і аналіз графіків функцій. Графіком функції f називається геометричне місце (множина) точок на координатній площині, які мають координати 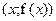, у яких абсцисами слугують значення незалежної змінної х, а ординатами – відповідні значення функції . Функції характеризуються рядом властивостей, до важливіших з яких (для побудови і дослідження графіків) відносяться: парність, нулі, періодичність, монотонність, обмеженість функції, наявність у функції асимптот і оберненої функції.

Функція називається парною, якщо для будь-яких двох різних значень аргументу із області її визначення виконується рівність 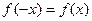(наприклад, 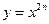, 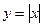). Функція називається непарною, якщо для будь-якого значення аргументу із області визначення функції виконується рівність 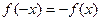(наприклад, 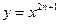). Існують функції, які не можна віднести до парних або непарних – аморфні (наприклад, 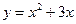). Графік парної функції симетричний відносно вісі OY, а непарної – відносно центру О.

Нулі функції. Нулями функції називають те значення аргументу, при якому функція набуває нульового значення. Графічно нулями функції є точки перетину графіку функції з віссю абсцис.

Періодичні функції. Функція називається періодичною, якщо існує число Т таке, що для кожного значення аргументу х з області її завдання має місце рівність 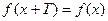. Число Т називають періодом функції.

Монотонність функції. Функція називається зростаючою на деякому проміжку, якщо для будь-яких значень х з цього проміжку, більшому значенню аргументу, відповідає більше значення функції. Функція називається спадною (спадаючою) на деякому проміжку, якщо для будь-яких значень х з цього проміжку, більшому значенню аргументу відповідає менше значення функції. Зростаючі та спадаючі функції називаються монотонними.

Асимптоти. Асимптотою графіка функції називається пряма, до якої наближається графік даної функції при прямуванні аргументу до нескінченності або до деякого числа а. Асимптоти можуть бути вертикальними, горизонтальними або похилими.

Обмежені функції. Функція називається обмеженою зверху (знизу), якщо існує таке число М, що для всіх х з області визначення . Функція називається обмеженою, якщо існує таке число М>0, що для всіх х з області визначення .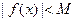

Обернена функція і її графік. Дана функція . Виразимо х як деяку функцію від у: 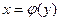, тобто представимо у як аргумент, а х – як функцію. Тоді функція 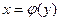називається оберненою по відношенню до функції , якщо при підстановці її замість аргументу отримуємо тотожну рівність: .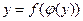

Складна функція. Функція, задана у вигляді 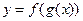, називається складною функцією х або суперпозицією функцій g та f.

Дата добавления: 2014-11-18